Определённый интеграл. Вычисление площади криволинейной трапеции презентация

ПОВТОРИМ!
1. Функция F(х) называется первообразной функции f(x) на некотором промежутке, если для всех Х из этого промежутка выполняется равенство:
2. F(x)+C, где С произвольная постоянная (любое число), называется семейством первообразных.
Другими словами нахождение первообразной – это обратное действие нахождения производной.
3. Совокупность всех первообразных данной функции f(x) называется неопределённым интегралом и обозначается:

Таблица первообразных
Правила нахождения первообразных

Найди ошибку в вычислении первообразных

Найдите первообразную функции

Фигура, ограниченная неотрицательной на отрезке [a;b] функцией y=f(x) и прямыми у=0, x=a, x=b называется
криволинейной трапецией.
Понятие криволинейной трапеции

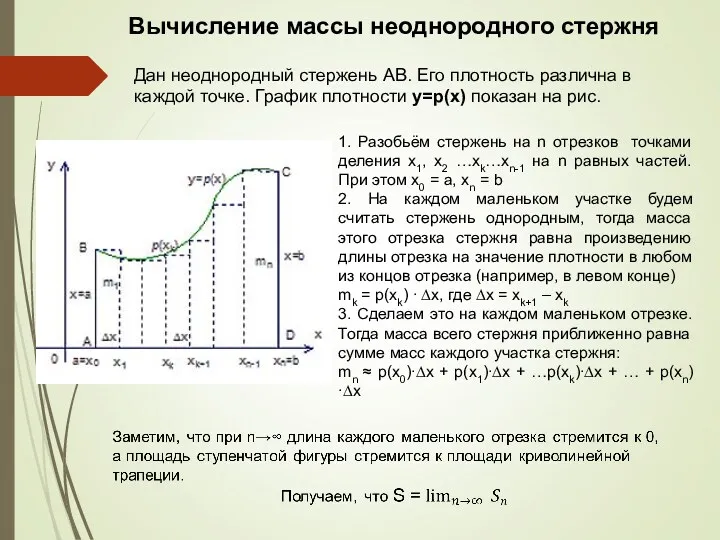
Разобьем отрезок [а;b] точками деления
х1, х2 …хk…xn-1 на n равных частей. При этом х0 = а, хn = b
Рассмотрим прямоугольник с основанием хk xk+1
Заменим площадь криволинейной трапеции на этом участке площадью этого прямоугольника.
Sk = f(xk) ∙ ∆x, где ∆x = xk+1 - хk
Сделаем это на каждом маленьком отрезке.
Тогда площадь криволинейной трапеции приближенно равна площади ступенчатой фигуры
Sn ≈ f(x0)∙∆x + f(x1)∙∆x + …f(xk)∙∆x + … + f(xn)∙∆x
Вычисление площади криволинейной трапеции

Вычисление массы неоднородного стержня
Дан неоднородный стержень АВ. Его плотность различна в каждой точке. График плотности у=р(х) показан на рис.
1. Разобьём стержень на n отрезков точками деления х1, х2 …хk…xn-1 на n равных частей. При этом х0 = а, хn = b
2. На каждом маленьком участке будем считать стержень однородным, тогда масса этого отрезка стержня равна произведению длины отрезка на значение плотности в любом из концов отрезка (например, в левом конце)
mk = р(xk) ∙ ∆x, где ∆x = xk+1 – хk
3. Сделаем это на каждом маленьком отрезке. Тогда масса всего стержня приближенно равна сумме масс каждого участка стержня:
mn ≈ p(x0)∙∆x + p(x1)∙∆x + …p(xk)∙∆x + … + p(xn)∙∆x

Подынтегральное выражение
Верхний предел интегрирования
Нижний предел интегрирования
Обобщение. Определение интеграла
Подынтегральная функция
Геометрический смысл определенного интеграла – площадь криволинейной трапеции под графиком подынтегральной функции

Вопрос:
Оказывается, есть прямая связь между этими понятиями!

Площадь криволинейной трапеции можно вычислить по формуле:
Где F(x) – первообразная функции y=f(x)
Вычисление площади криволинейной трапеции сводится к отысканию первообразной F(x) функции f(x), то есть к интегрированию функции f(x).
Формула Ньютона-Лейбница

Формула Ньютона - Лейбница
Исаак Ньютон
1642-1727
Готфрид Лейбниц
1646-1716 гг.
Таким образом:

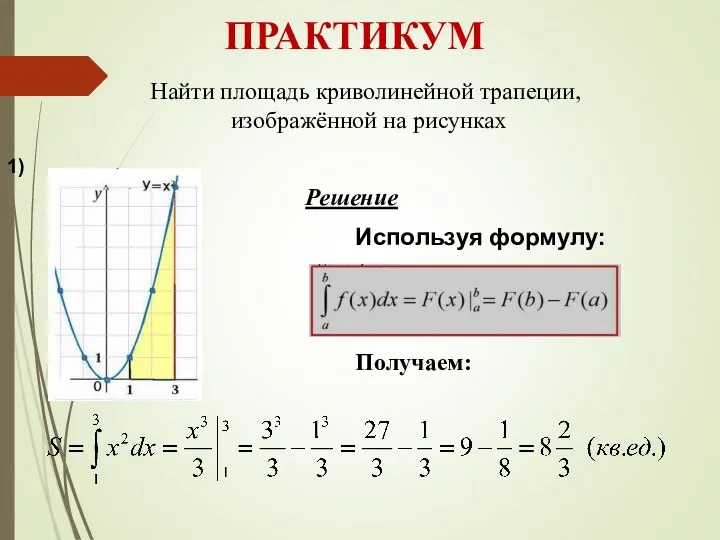
ПРАКТИКУМ
Найти площадь криволинейной трапеции,
изображённой на рисунках
Используя формулу:
Решение
Получаем:
1)

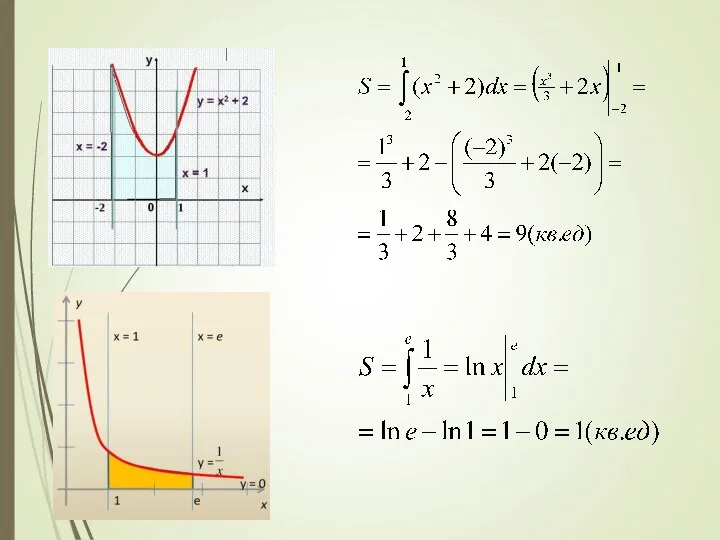
Вычисление площадей с помощью интегралов
1. Криволинейная трапеция, ограниченная сверху графиком функции y=f(x), снизу осью ОХ и прямыми х=а, х=в

2. Фигура, ограниченная сверху только графиком функции y=f(x) и снизу осью ОХ
Точки а и b находим из уравнения f(x) =0
3. Криволинейная трапеция, ограниченная сверху осью ОХ, снизу графиком функции y=f(x) и прямыми х = а, х=в

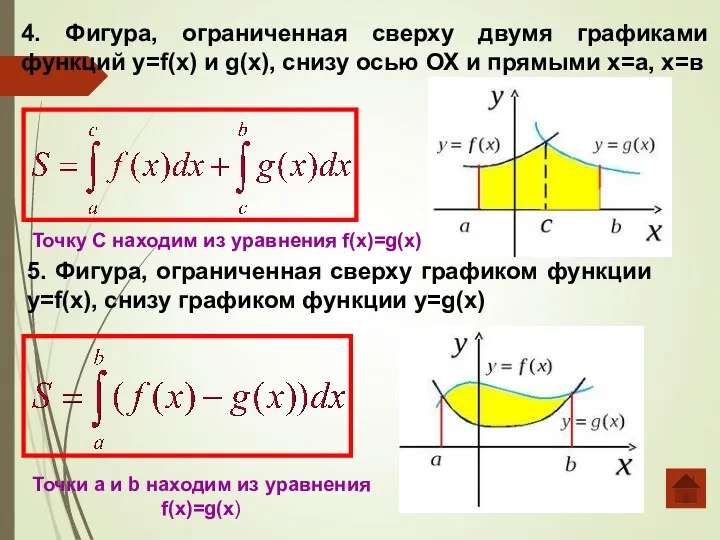
4. Фигура, ограниченная сверху двумя графиками функций y=f(x) и g(x), снизу осью ОХ и прямыми х=а, х=в
Точку С находим из уравнения f(x)=g(x)
5. Фигура, ограниченная сверху графиком функции y=f(x), снизу графиком функции y=g(x)
Точки a и b находим из уравнения f(x)=g(x)

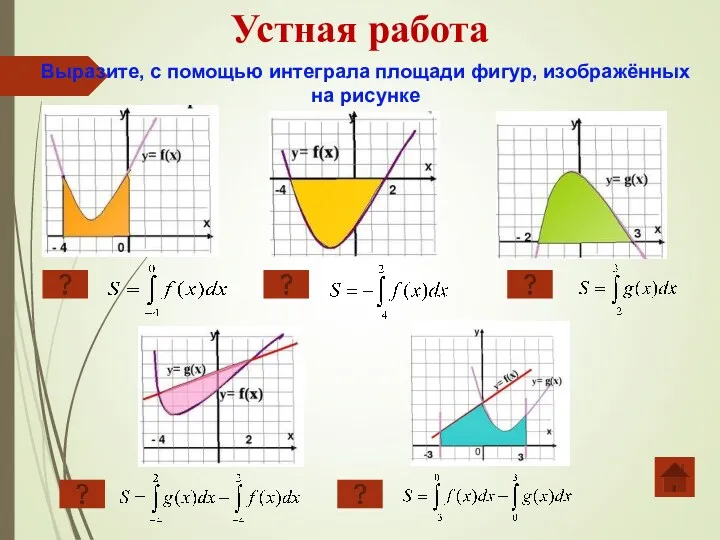
Устная работа
Выразите, с помощью интеграла площади фигур, изображённых на рисунке

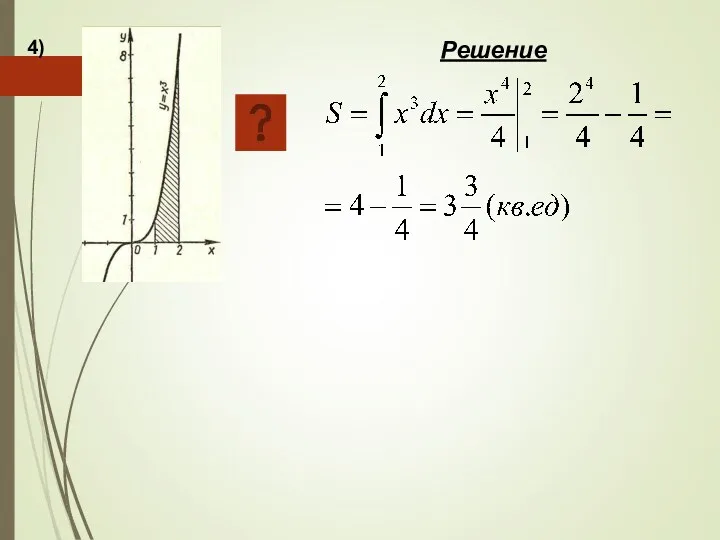
4)
Решение

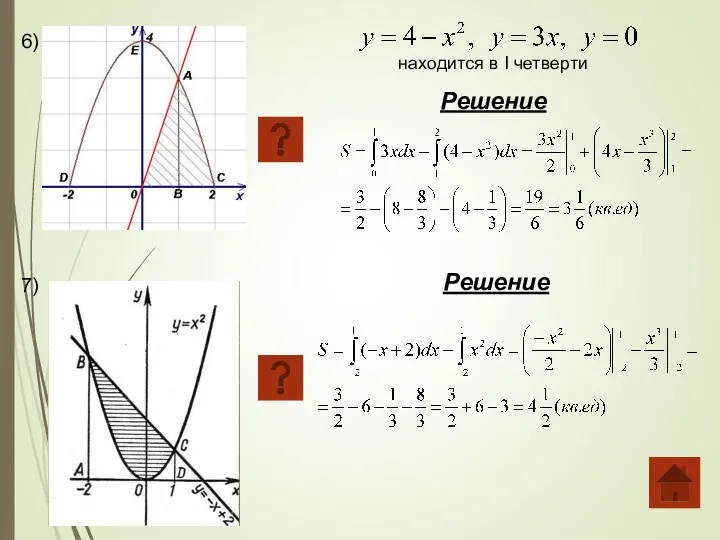
6)
находится в I четверти
Решение
7)
Решение

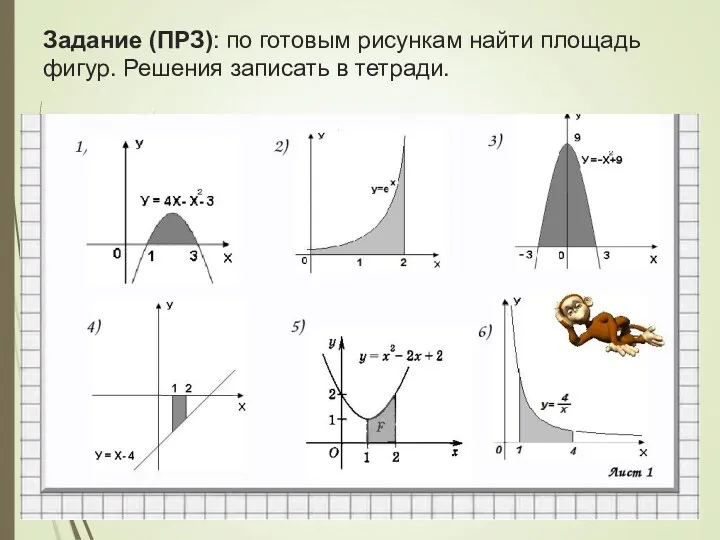
Задание (ПРЗ): по готовым рисункам найти площадь фигур. Решения записать в тетради.

Домашнее задание
Вычислить площадь фигуры, ограниченной линиями, предварительно сделав рисунок