Содержание
- 2. Определение. Уравнение вида ах⁴+bх²+с=0, где а, b и с –данные числа и а≠0, а х -
- 3. Алгоритм решения биквадратного уравнения: Введем в уравнение новую переменную путем обозначения какого- то выражения из этого
- 4. 3) Решаем полученное квадратное уравнение; 4) Способом подстановки находим значение исходной переменной; 5) С помощью проверки
- 5. Пример 1: х⁴-4х²+3=0 Пусть х²=t тогда получим уравнение t²-4t+3=0 t₁=3 t₂=1 1)x²=3 2)x²=1 X=± x=±1 Ответ:
- 6. Пример 2: x⁴-2x²-2=0 t²-2t-2=0, по формуле корней приведенного квадратного уравнения, получим 1)x²=1+ 2)x²=1- x₁,₂=± нет корней,
- 7. Пример 3: 2х⁴-3х²+5=0 2t²-3t+5=0 Корней нет, т.к. Ответ: корней нет. Пусть х²=t тогда получим уравнение
- 8. Пример 4: 9х⁴-6х²+1=0 (3х²-1)²=0 3х²-1=0 х²= х=± Ответ: х₁,₂=± Применим формулу квадрат разности, тогда получим уравнение
- 10. Скачать презентацию







 группа
группа Координатная плоскость
Координатная плоскость Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли
Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли Решение задач на части. 5 класс
Решение задач на части. 5 класс Вычитание вида 17-[], 18-[]
Вычитание вида 17-[], 18-[] Понятие средней величины. Виды средних величин
Понятие средней величины. Виды средних величин Закрепление счёта в пределах 10.
Закрепление счёта в пределах 10. Вычитание чисел
Вычитание чисел Сложение и вычитание одночленов
Сложение и вычитание одночленов Действия с многозначными числами (устные вычисления).
Действия с многозначными числами (устные вычисления). Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка
Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка Признаки параллельных прямых. 7 класс
Признаки параллельных прямых. 7 класс Мерительный инструмент
Мерительный инструмент Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками Нахождение процентов от числа и числа по его проценту
Нахождение процентов от числа и числа по его проценту Смешанные дроби
Смешанные дроби Из истории дроби. Современное обозначение дробей
Из истории дроби. Современное обозначение дробей Графический способ решения системы уравнений с двумя переменными
Графический способ решения системы уравнений с двумя переменными Игра Математик - бизнесмен. 10-11 классы
Игра Математик - бизнесмен. 10-11 классы Кут та його величина. Види кутів (5 клас)
Кут та його величина. Види кутів (5 клас) Формирование основных компетенций на уроках математики
Формирование основных компетенций на уроках математики Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems
Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems Подобные треугольники (8 класс)
Подобные треугольники (8 класс) Весёлые числа (часть 2)
Весёлые числа (часть 2) С Бибигоном на Луну
С Бибигоном на Луну Математика – білім негізі
Математика – білім негізі Урок математики Числа от 1 до 10. Закрепление
Урок математики Числа от 1 до 10. Закрепление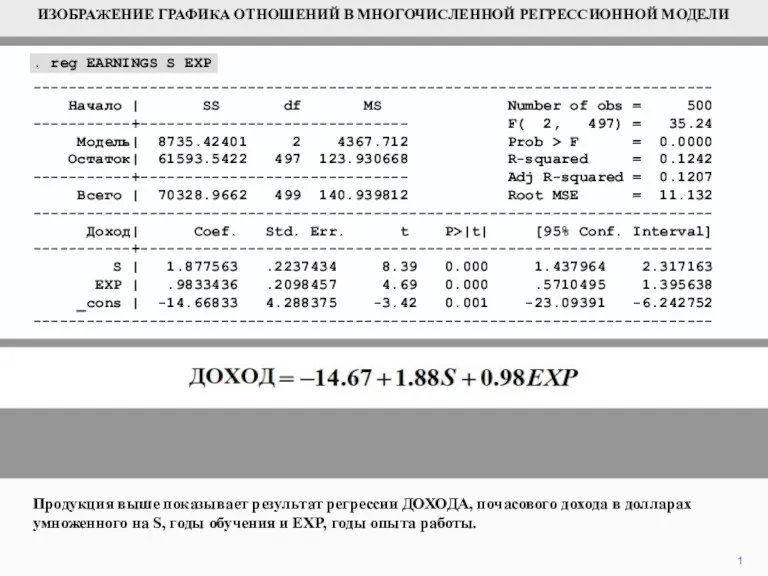 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели