Содержание
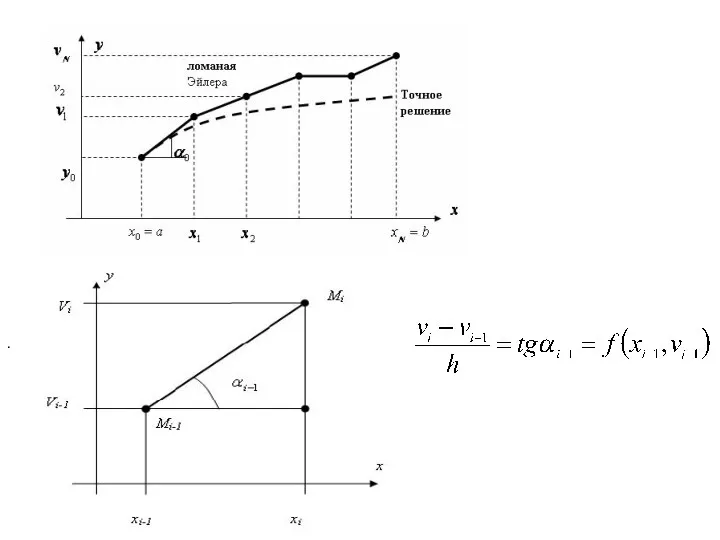
- 2. 1.Понятие о методе Эйлера (геометрическая интерпретация) Решение начальных задач с дифференциальными уравнениями является необходимым этапом математического
- 3. Систему уравнений называют явной схемой Эйлера. Эта система приводится к рекуррентным формулам При изучении свойств метода
- 4. , .
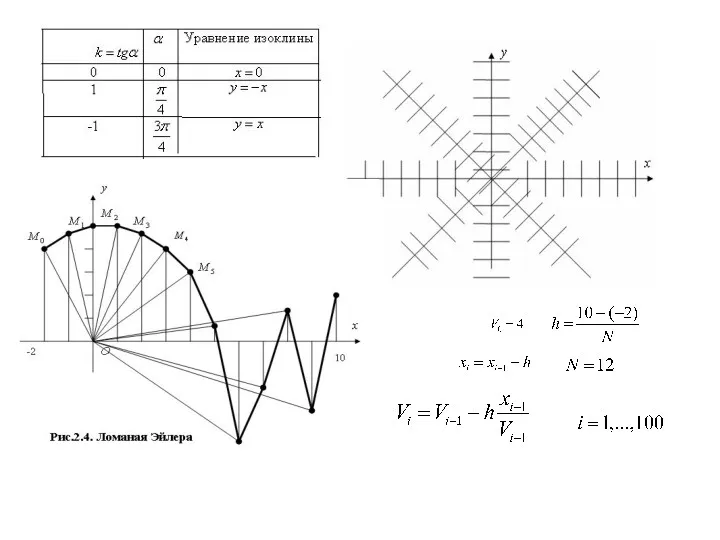
- 5. 2. Особенности реализации метода Эйлера в системе Mathcad Рассмотрим задачу Точное решение задачи имеет вид Построим
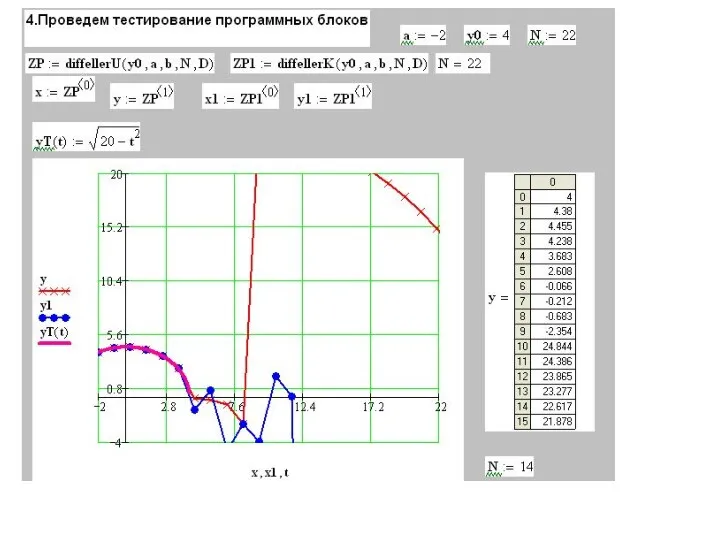
- 7. Реализация явной схемы Эйлера в системе Mathcad
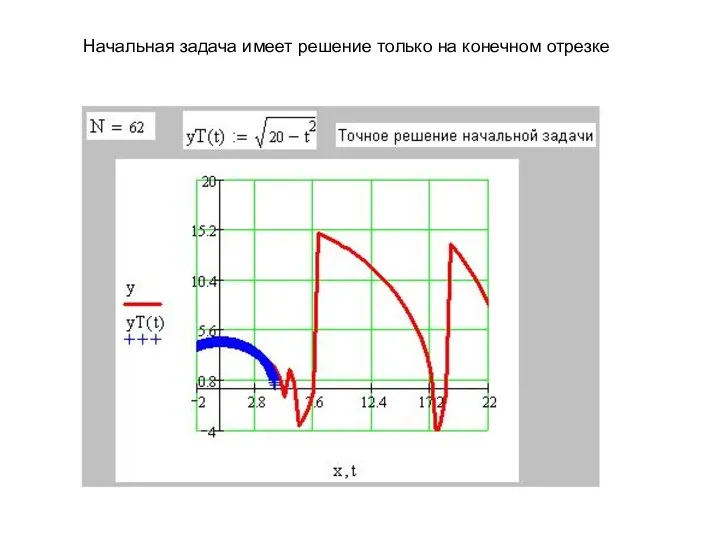
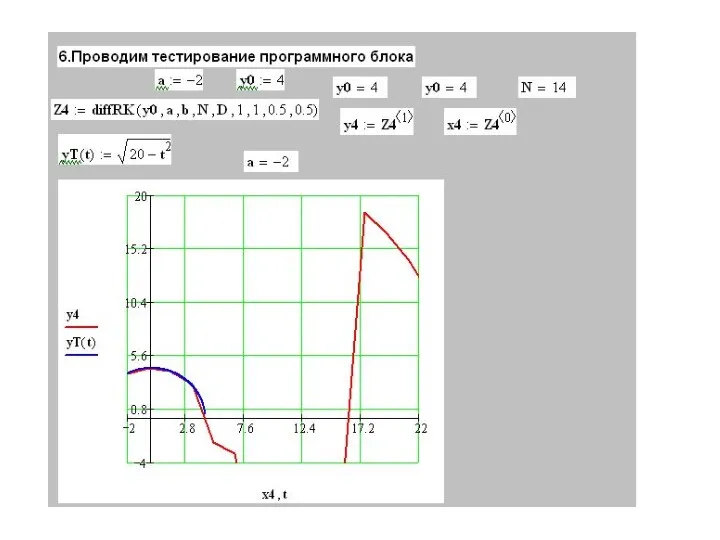
- 8. Начальная задача имеет решение только на конечном отрезке
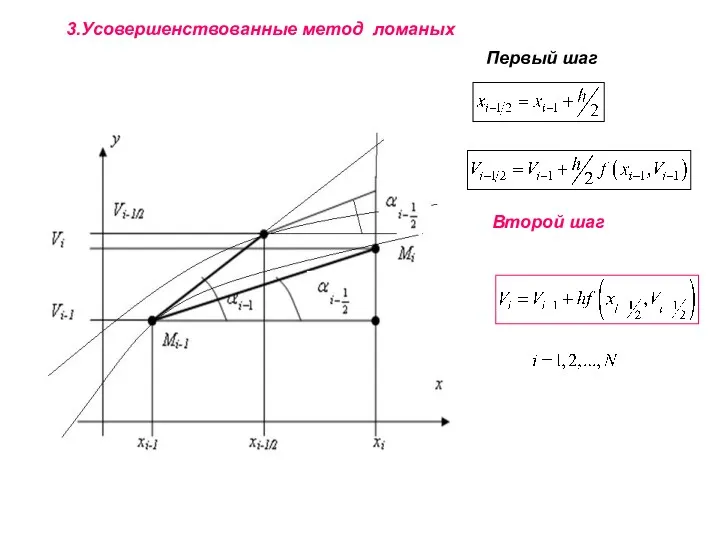
- 9. 3.Усовершенствованные метод ломаных Первый шаг Второй шаг
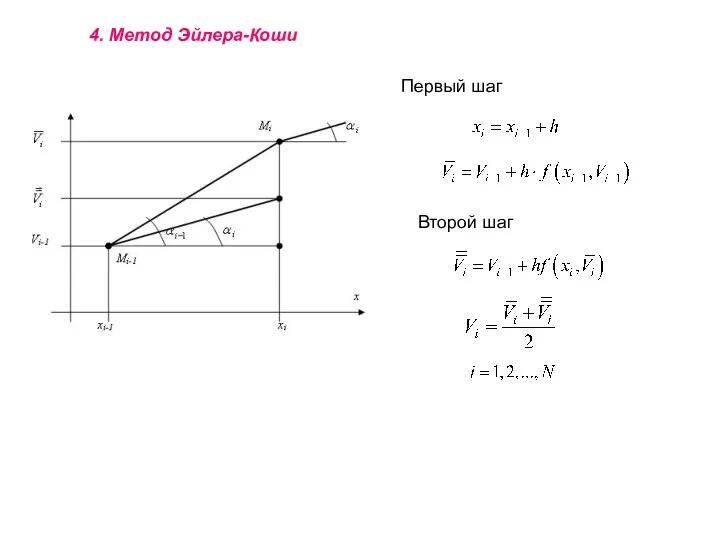
- 11. 4. Метод Эйлера-Коши Первый шаг Второй шаг
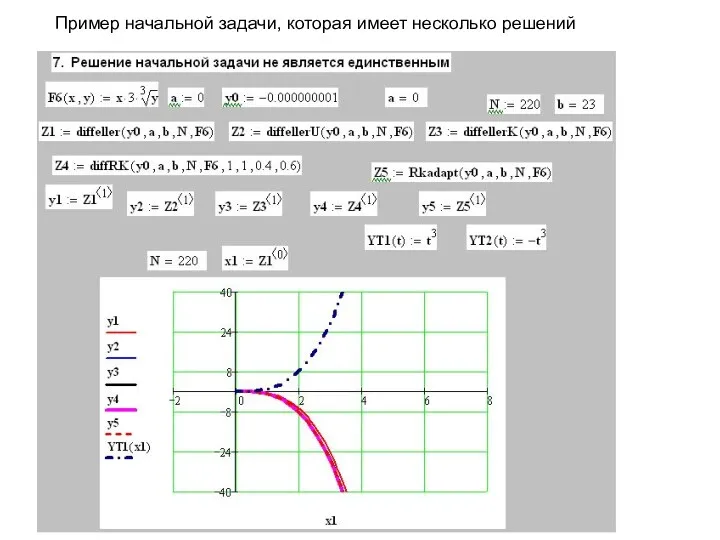
- 14. Пример начальной задачи, которая имеет несколько решений
- 15. 5.Аппроксимация производных разностными отношениями. Порядок аппроксимации Сеткой на отрезке [a, b] называют любое конечное множество точек
- 16. Рассмотрим погрешность замены производной разностными отношениями (погрешность аппроксимации) Формула Тейлора в форме Лагранжа имеет вид Бесконечно
- 17. Пусть функция обладает необходимой гладкостью тогда и в точке xi Отсюда получаем Разностные отношения аппроксимируют производные
- 18. Центральное разностное отношение аппроксимирует производную со вторым порядком Замечание. В дальнейшем используются обозначения.
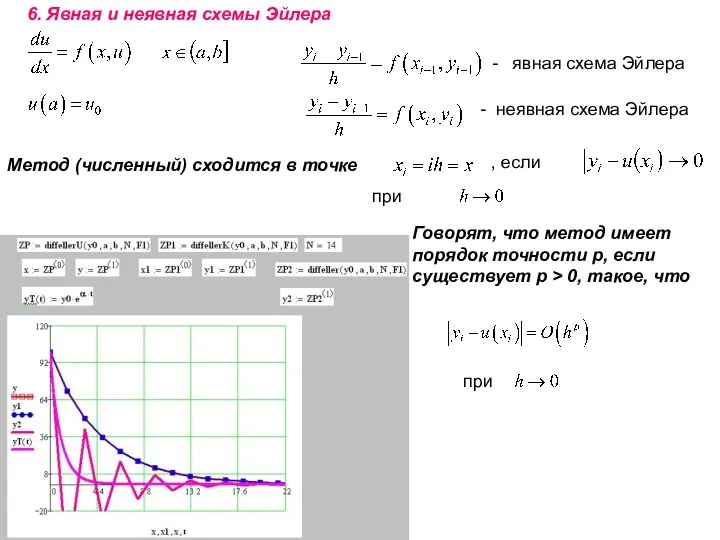
- 19. - явная схема Эйлера - неявная схема Эйлера 6. Явная и неявная схемы Эйлера Говорят, что
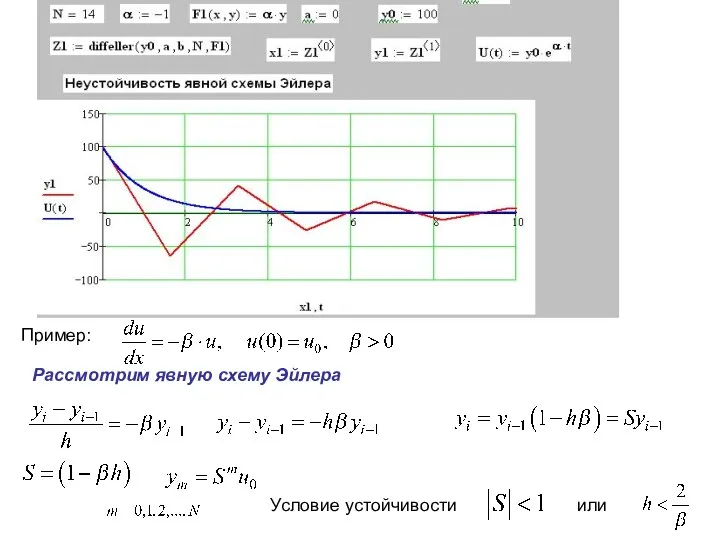
- 20. Рассмотрим явную схему Эйлера Условие устойчивости или Пример:
- 21. Отсюда следует При любом h значения ym уменьшаются с ростом m. Это соответствует убыванию точного решения
- 22. 7. Методы Рунге-Кутта и их реализация в системе Mathcad Схема Эйлера - Коши
- 25. Скачать презентацию












 Обыкновенные дроби. (Урок 48)
Обыкновенные дроби. (Урок 48) Функция y=k/x, её график и свойства
Функция y=k/x, её график и свойства Сложение вида +7
Сложение вида +7 Гексаэдр (куб)
Гексаэдр (куб) Смешанные числа
Смешанные числа Подготовка к ВПР по математике
Подготовка к ВПР по математике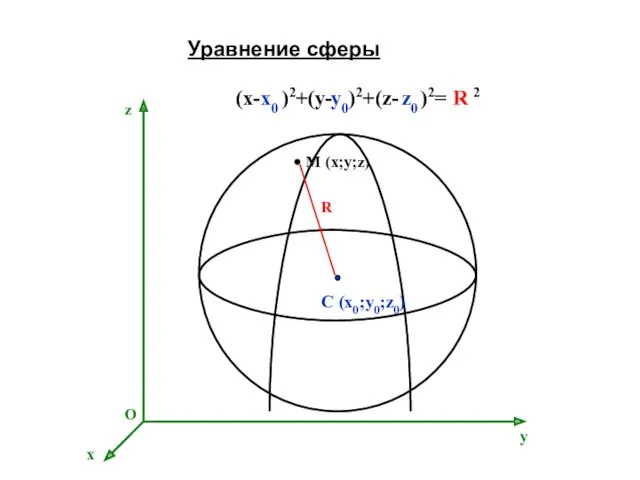 Уравнение сферы
Уравнение сферы игра-тренажёрПомоги ёжику
игра-тренажёрПомоги ёжику Игры для детей
Игры для детей Признаки делимости чисел на 2, 3, 9
Признаки делимости чисел на 2, 3, 9 Угол между векторами
Угол между векторами Степенная функция. 9 класс
Степенная функция. 9 класс Перст. Старинные единицы меры длины
Перст. Старинные единицы меры длины Тетраэдр. Задания для устного счета. Упражнение 5
Тетраэдр. Задания для устного счета. Упражнение 5 Прямая и обратная пропорциональные зависимости. (6 класс)
Прямая и обратная пропорциональные зависимости. (6 класс) Четные и нечетные числа
Четные и нечетные числа Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей ОГЭ. Колеса
ОГЭ. Колеса Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Устный счет
Устный счет Математика вокруг нас для детей подготовительной к школе группы
Математика вокруг нас для детей подготовительной к школе группы Метод конечных элементов
Метод конечных элементов Предмет геометрии. Аксиомы геометрии
Предмет геометрии. Аксиомы геометрии Зурлыклар белән гамәлләртемасына математика дәресенә презентация
Зурлыклар белән гамәлләртемасына математика дәресенә презентация Взаимно обратные функции
Взаимно обратные функции Признак перпендикулярности прямой и плоскости
Признак перпендикулярности прямой и плоскости Решение иррациональных уравнений. 11 класс
Решение иррациональных уравнений. 11 класс Турнир юных математиков
Турнир юных математиков