Содержание
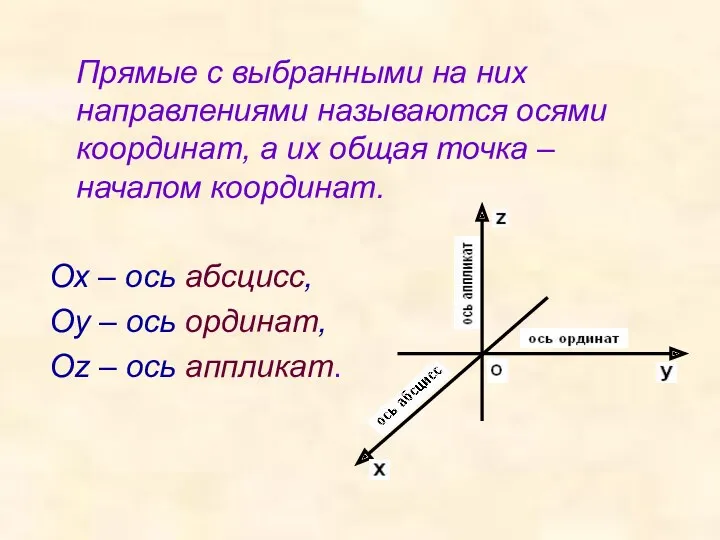
- 2. Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.
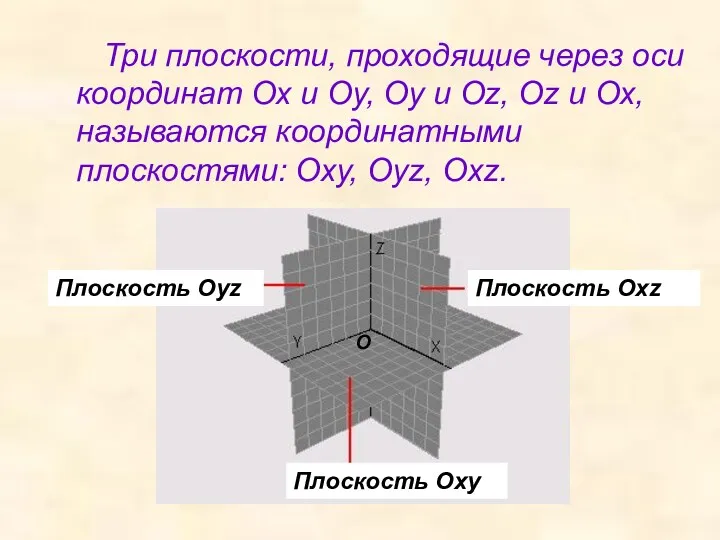
- 3. Три плоскости, проходящие через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются
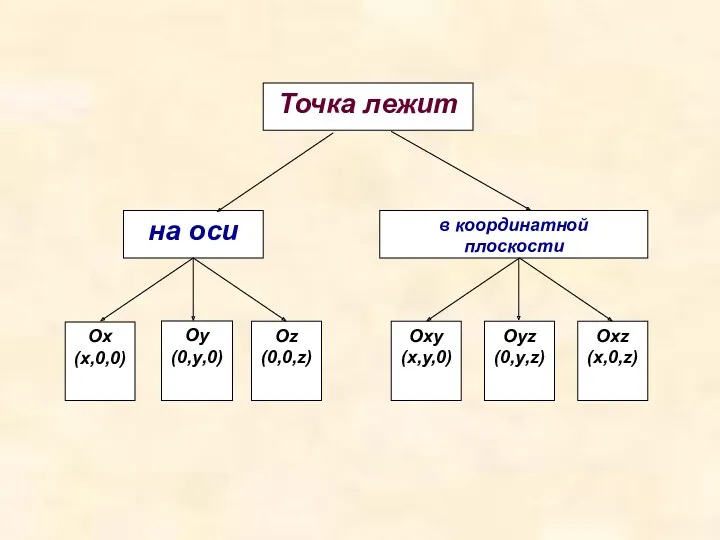
- 4. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты: М (х,
- 5. Оу (0,у,0)
- 6. Координаты вектора в пространстве
- 7. Единичный вектор – вектор, длина которого равна 1. i – единичный вектор оси абсцисс, j –
- 8. Любой вектор ā можно разложить по координатным векторам, т.е. представить в виде: Нулевой вектор можно представить
- 9. Сумма векторов: a + b = { x1+ x2; y1+ y2; z1+ z2 }. Разность векторов:
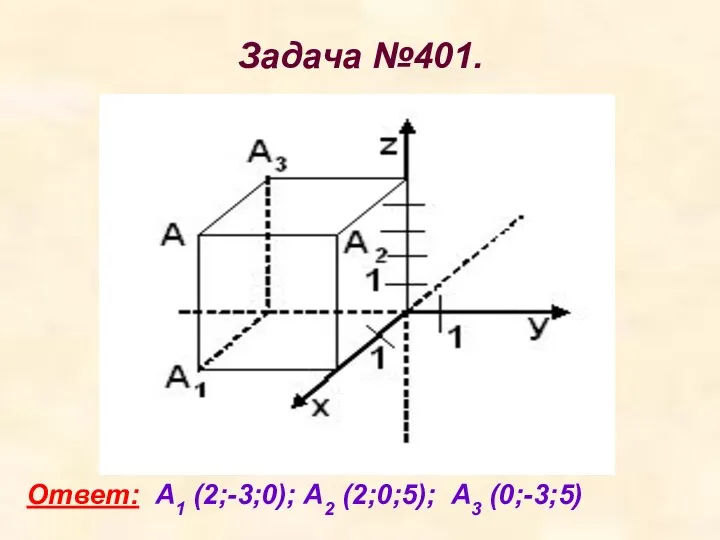
- 10. Задача №401. Ответ: А1 (2;-3;0); А2 (2;0;5); А3 (0;-3;5)
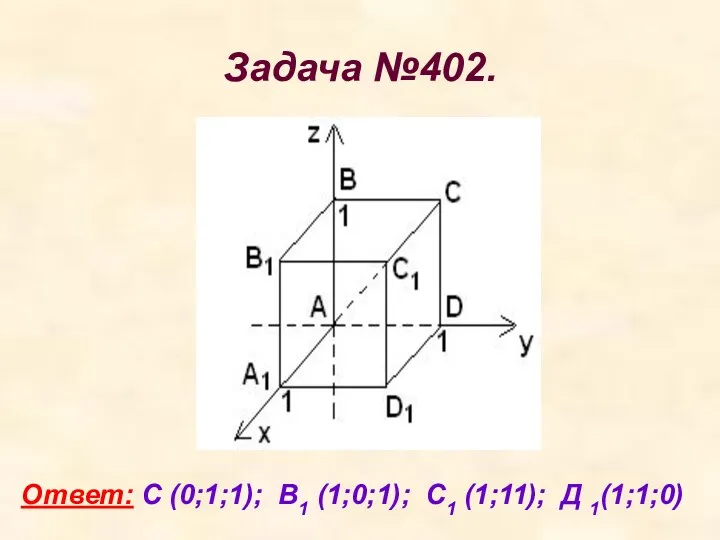
- 11. Задача №402. Ответ: С (0;1;1); В1 (1;0;1); С1 (1;11); Д 1(1;1;0)
- 12. Итог урока На уроке познакомились с прямоугольной системой координат, научились строить точку по заданным ее координатам
- 13. Разложение вектора по координатным векторам
- 14. Векторы называются коллинеарными, если они параллельны. Если векторы а { x1; y1; z1 } и b
- 15. Самостоятельная работа 1 вариант №1. Даны векторы а {2; -4; 3} и b {-3; 1/2; 1}.
- 16. Связь между координатами векторов и координатами точек
- 17. Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной
- 18. Простейшие задачи в координатах
- 19. 1. Координаты середины отрезка. О А В С D х у z A (x1; y1; z1),
- 20. Угол между векторами
- 21. О А В α Если а || b и а и b сонаправлены, то α =
- 22. Скалярное произведение векторов
- 23. a · b = | a | · | b | · cos(a ^ b) 2)
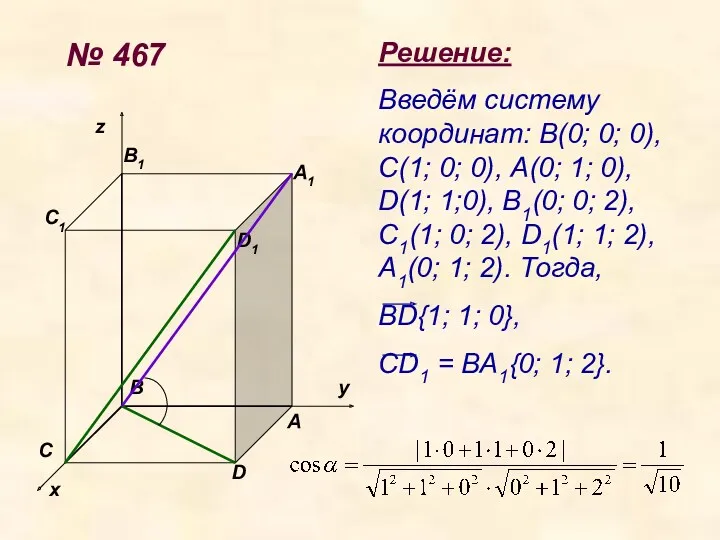
- 24. № 467 х у z A B C D D1 A1 B1 C1 Решение: Введём систему
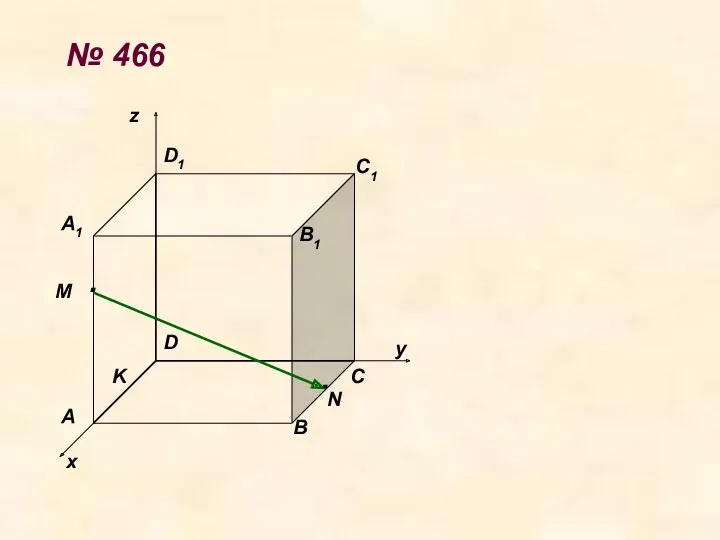
- 25. № 466 A х у z B C D A1 B1 C1 D1 M K .
- 27. Скачать презентацию















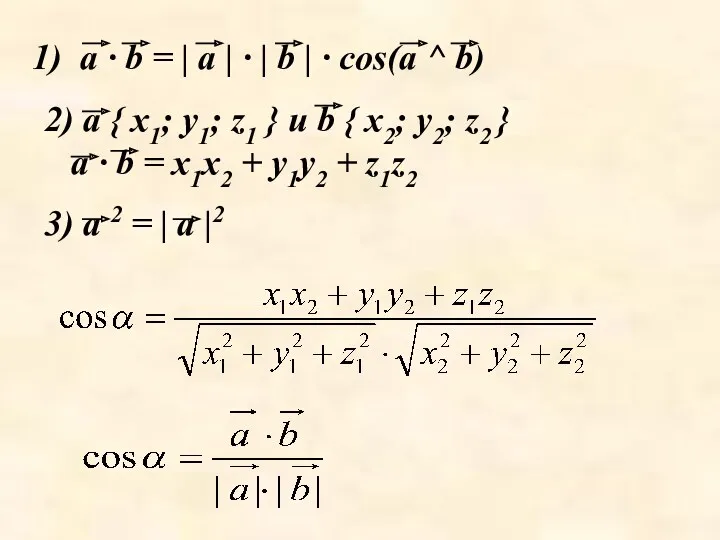
 Многоугольник
Многоугольник Решение тригонометрических уравнений
Решение тригонометрических уравнений Формулы сокращённого умножения. 7 класс
Формулы сокращённого умножения. 7 класс Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5
Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5 Преобразования. Оконное преобразование Фурье. Области применения и ограничения оконного преобразования Фурье
Преобразования. Оконное преобразование Фурье. Области применения и ограничения оконного преобразования Фурье презентация к конспекту по математике Прибавление числа 5
презентация к конспекту по математике Прибавление числа 5 Уравнение. Корень уравнения
Уравнение. Корень уравнения Математика и в шутку и всерьёз
Математика и в шутку и всерьёз Урок - практикум по решению задач части Геометрия ОГЭ по математике
Урок - практикум по решению задач части Геометрия ОГЭ по математике Великие математики древности
Великие математики древности Геометрические понятия. Плакат.
Геометрические понятия. Плакат. Математика Свойства вычитания
Математика Свойства вычитания Дополнительные платные образовательные, досуговые и оздоровительные услуги. 2019-2020 учебный год
Дополнительные платные образовательные, досуговые и оздоровительные услуги. 2019-2020 учебный год Урок-игра по математике
Урок-игра по математике Математический КВН
Математический КВН Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса
Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса Набор 2023. Вступительные задания по математике
Набор 2023. Вступительные задания по математике Угол. Прямой и развернутый угол. Чертежный треугольник
Угол. Прямой и развернутый угол. Чертежный треугольник Открытый урок по математике в 3-м классе Единица времени - сутки
Открытый урок по математике в 3-м классе Единица времени - сутки Решение задач.3 класс, УМК Гармония.
Решение задач.3 класс, УМК Гармония. Урок математики во 2 классе 2100
Урок математики во 2 классе 2100 Координатная плоскость
Координатная плоскость Действительные числа. Степенная функция. Материалы по математике для обучающихся 10-11 класса
Действительные числа. Степенная функция. Материалы по математике для обучающихся 10-11 класса Симметрия. Центральная и осевая симметрии
Симметрия. Центральная и осевая симметрии Урок. Задачи на движение.
Урок. Задачи на движение. Сложение и вычитание десятичных дробей. Урок математики в 5 классе
Сложение и вычитание десятичных дробей. Урок математики в 5 классе математика
математика Каскады из правильных многогранников
Каскады из правильных многогранников