Содержание
- 2. Frequency Distributions and Their Graphs Section 2.1
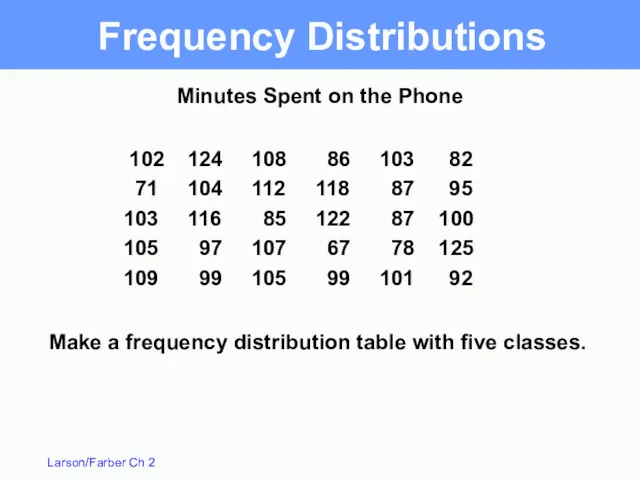
- 3. Frequency Distributions 102 124 108 86 103 82 71 104 112 118 87 95 103 116
- 4. Frequency Distributions Classes - the intervals used in the distribution Class width - the range divided
- 5. Frequency Distributions Midpoint - the sum of the limits divided by 2 lower class limit +
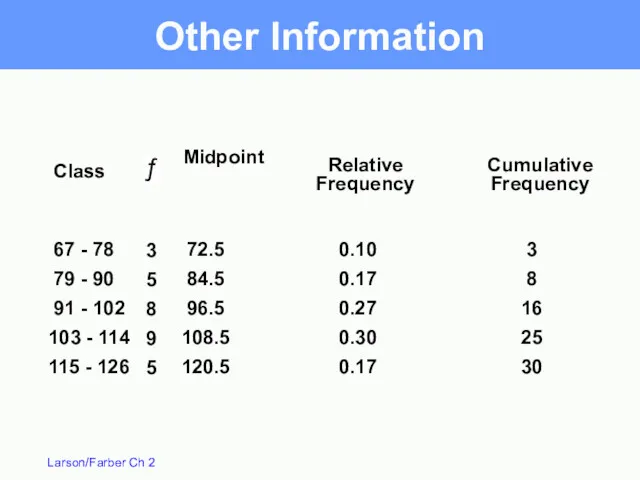
- 6. 78 90 102 114 126 3 5 8 9 5 67 79 91 103 115 Do
- 7. 67 - 78 79 - 90 91 - 102 103 - 114 115 - 126 3
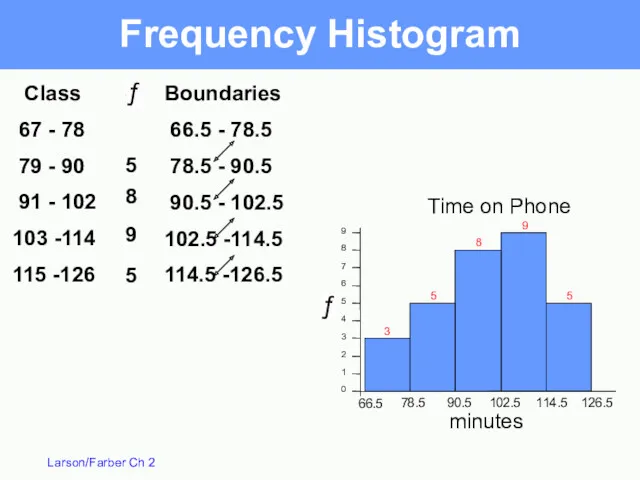
- 8. Frequency Histogram A bar graph that represents the frequency distribution of the data set horizontal scale
- 9. 1 2 6 . 5 1 1 4 . 5 1 0 2 . 5 9
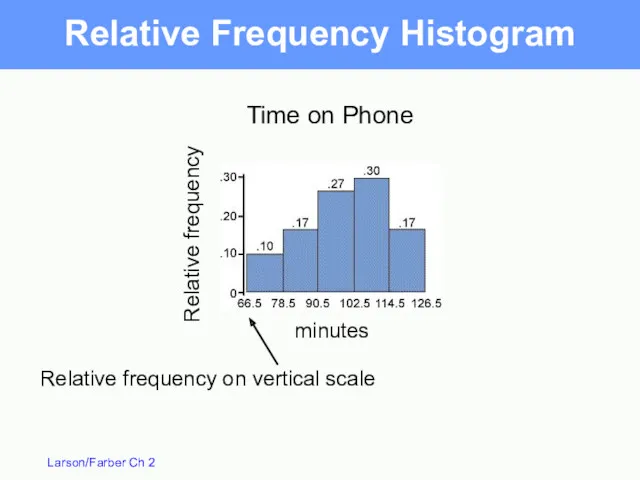
- 10. Relative Frequency Histogram A bar graph that represents the relative frequency distribution of the data set
- 11. Relative Frequency Histogram Time on Phone minutes Relative frequency on vertical scale Relative frequency
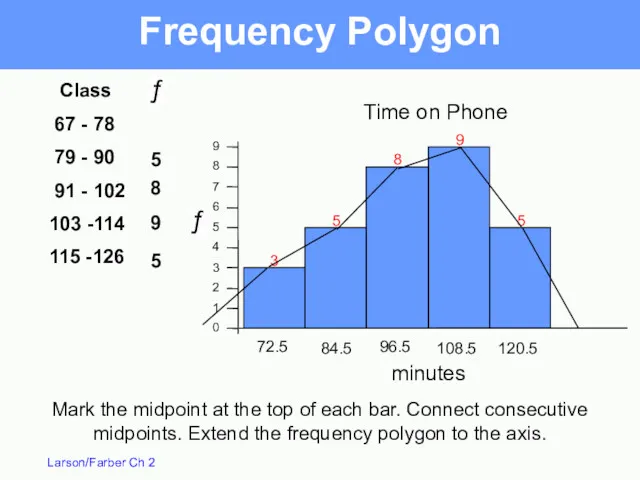
- 12. Frequency Polygon A line graph that emphasizes the continuous change in frequencies horizontal scale uses class
- 13. Frequency Polygon 9 8 7 6 5 4 3 2 1 0 5 9 8 5
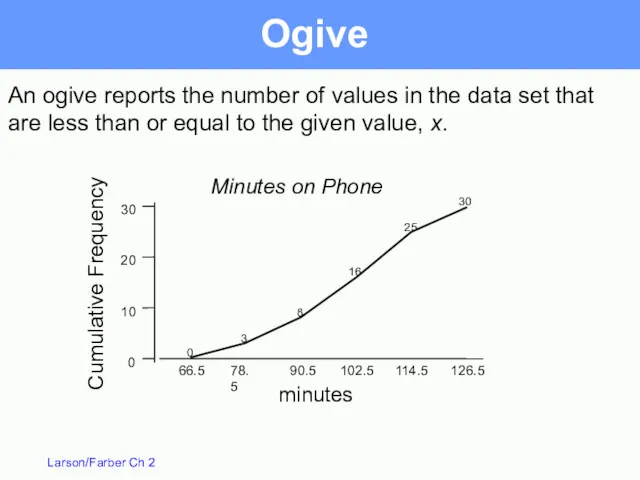
- 14. Ogive Also called a cumulative frequency graph A line graph that displays the cumulative frequency of
- 15. Ogive An ogive reports the number of values in the data set that are less than
- 16. More Graphs and Displays Section 2.2
- 17. Stem-and-Leaf Plot 102 124 108 86 103 82 71 104 112 118 87 95 103 116
- 18. Stem-and-Leaf Plot 6 | 7 | 8 | 9 | 10 | 11 | 12 |
- 19. 6 | 7 7 | 1 8 8 | 2 5 6 7 7 9 |
- 20. Stem-and-Leaf with two lines per stem 6 | 7 7 | 1 7 | 8 8
- 21. Dot Plot 66 76 86 96 106 116 126 -contains all original data -easy way to
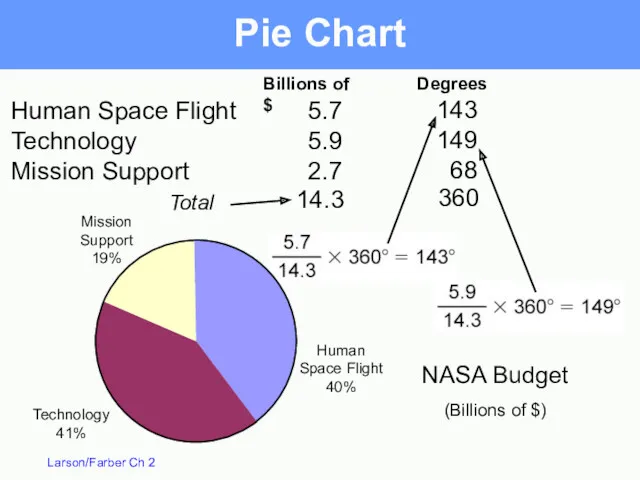
- 22. NASA budget (billions of $) divided among 3 categories. Pie Chart / Circle Graph Used to
- 23. Total Pie Chart Billions of $ Human Space Flight 5.7 Technology 5.9 Mission Support 2.7 14.3
- 24. Pareto Chart -A vertical bar graph in which the height of the bar represents frequency or
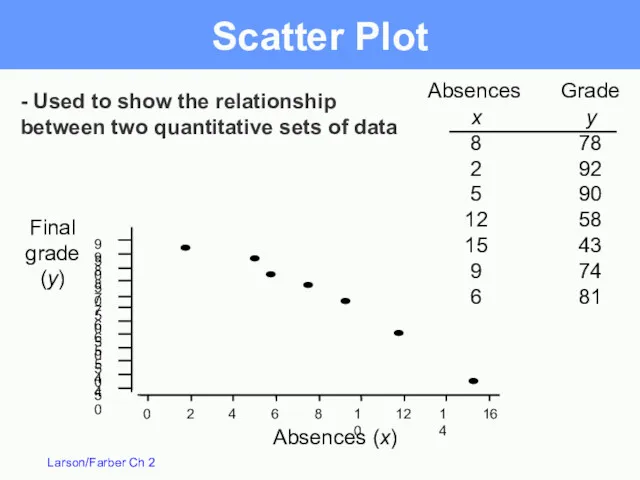
- 25. Scatter Plot Absences Grade Absences (x) x 8 2 5 12 15 9 6 y 78
- 26. Time Series Chart / Line Graph - Quantitative entries taken at regular intervals over a period
- 27. Measures of Central Tendency Section 2.3
- 28. Measures of Central Tendency Mean: The sum of all data values divided by the number of
- 29. 2 4 2 0 40 2 4 3 6 Calculate the mean, the median, and the
- 30. 0 2 2 2 3 4 4 6 40 2 4 2 0 40 2 4
- 31. Mode: The mode is 2 since it occurs the most times. Calculate the mean, the median,
- 32. Median: Sort data in order. Mode: The mode is 2 since it occurs the most times.
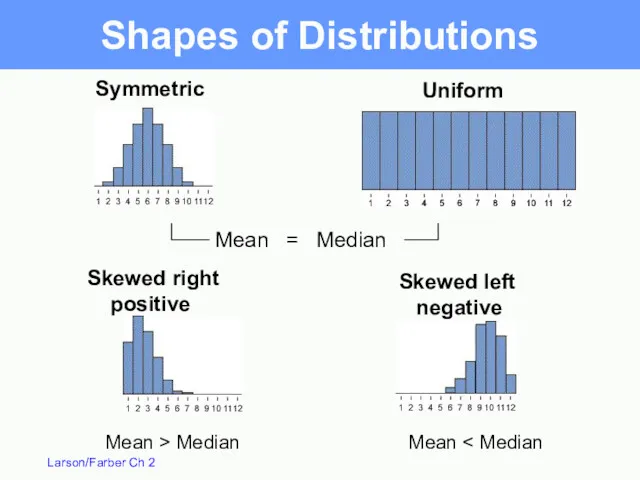
- 33. Uniform Symmetric Skewed right positive Skewed left negative Mean = Median Mean > Median Mean Shapes
- 34. A weighted mean is the mean of a data set whose entries have varying weights X
- 35. Weighted Mean A student receives the following grades, A worth 4 points, B worth 3 points,
- 36. The mean of a frequency distribution for a sample is approximated by X = where x
- 37. Mean of Grouped Data The heights of 16 students in a physical ed. class: Height Frequency
- 38. Measures of Variation Section 2.4
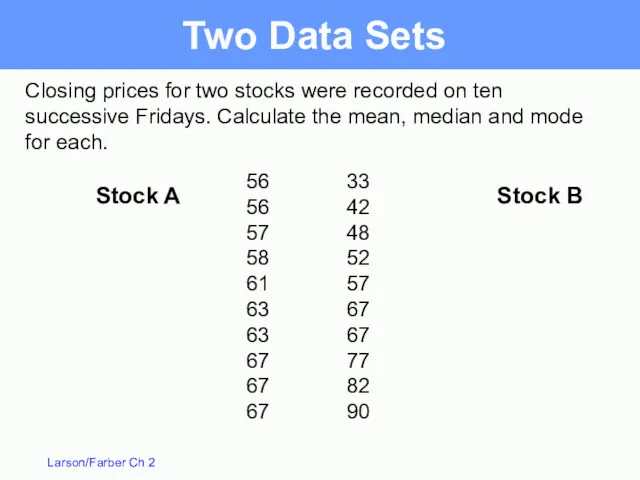
- 39. Closing prices for two stocks were recorded on ten successive Fridays. Calculate the mean, median and
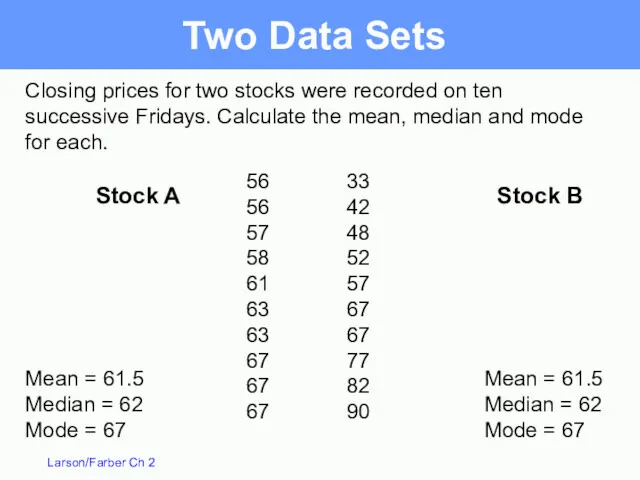
- 40. Closing prices for two stocks were recorded on ten successive Fridays. Calculate the mean, median and
- 41. Range for A = 67 – 56 = $11 Range = Maximum value – Minimum value
- 42. The deviation for each value x is the difference between the value of x and the
- 43. – 5.5 – 5.5 – 4.5 – 3.5 – 0.5 1.5 1.5 5.5 5.5 5.5 56
- 44. Population Variance Sum of squares – 5.5 – 5.5 – 4.5 – 3.5 – 0.5 1.5
- 45. Population Standard Deviation Population Standard Deviation: The square root of the population variance. The population standard
- 46. Sample Variance and Standard Deviation To calculate a sample variance divide the sum of squares by
- 47. Interpreting Standard Deviation Standard deviation is a measure of the typical amount an entry deviates (is
- 48. Summary Range = Maximum value – Minimum value
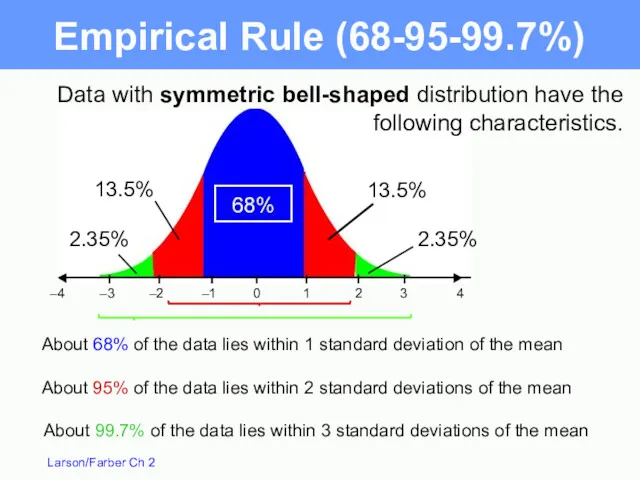
- 49. Data with symmetric bell-shaped distribution have the following characteristics. About 68% of the data lies within
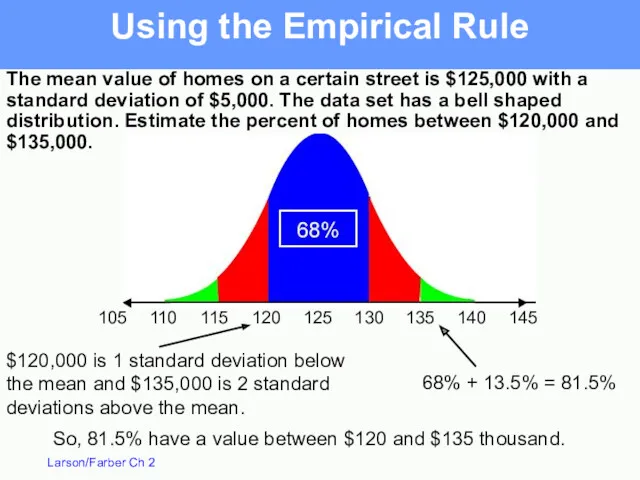
- 50. The mean value of homes on a certain street is $125,000 with a standard deviation of
- 51. The mean value of homes on a certain street is $125,000 with a standard deviation of
- 52. Chebychev’s Theorem For k = 3, at least 1 – 1/9 = 8/9 = 88.9% of
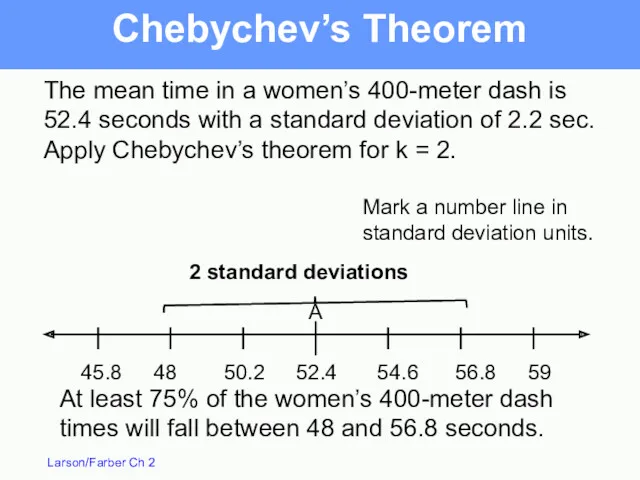
- 53. Chebychev’s Theorem The mean time in a women’s 400-meter dash is 52.4 seconds with a standard
- 54. Chebychev’s Theorem The mean time in a women’s 400-meter dash is 52.4 seconds with a standard
- 55. Standard Deviation of Grouped Data Sample standard deviation = See example on pg 82 f is
- 56. Estimates with Classes When a frequency distribution has classes, you can estimate the sample mean and
- 57. Measures of Position Section 2.5
- 58. Fractiles – numbers that divide an ordered data set into equal parts. Quartiles (Q1, Q2 and
- 59. You are managing a store. The average sale for each of 27 randomly selected days in
- 60. The data in ranked order (n = 27) are: 17 19 20 23 27 28 30
- 61. Interquartile Range – the difference between the third and first quartiles IQR = Q3 – Q1
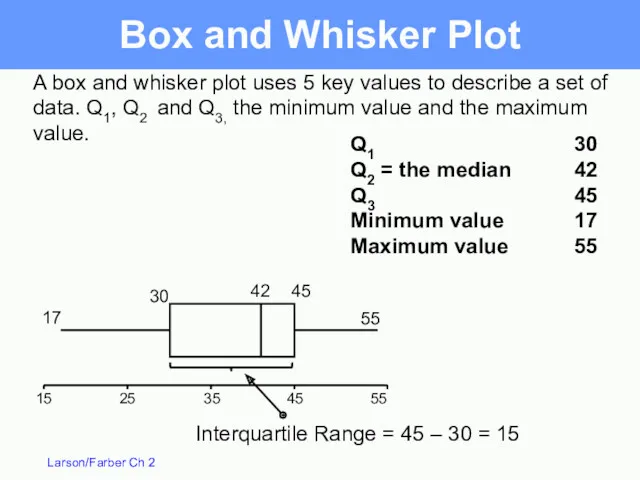
- 62. Box and Whisker Plot 55 45 35 25 15 A box and whisker plot uses 5
- 63. Percentiles Percentiles divide the data into 100 parts. There are 99 percentiles: P1, P2, P3…P99. A
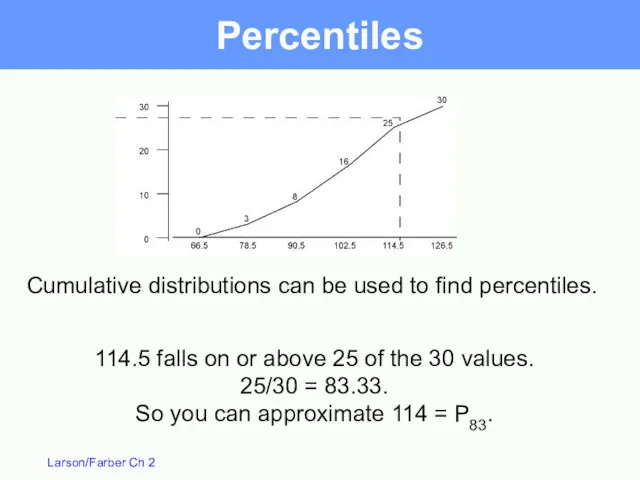
- 64. Percentiles 114.5 falls on or above 25 of the 30 values. 25/30 = 83.33. So you
- 65. Standard Scores Standard score or z-score - represents the number of standard deviations that a data
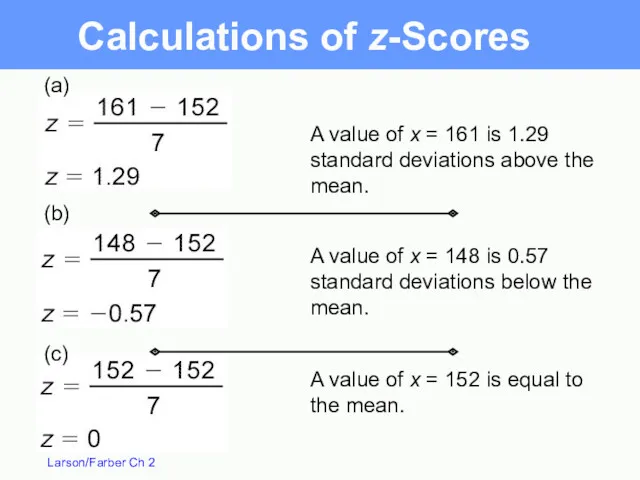
- 66. Standard Scores The test scores for a civil service exam have a mean of 152 and
- 67. (c) (a) (b) A value of x = 161 is 1.29 standard deviations above the mean.
- 69. Скачать презентацию

















































 Метод математической индукции
Метод математической индукции урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск
урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск Геометричні перетворення графіків функцій
Геометричні перетворення графіків функцій тест по математике №2 - 2 класс
тест по математике №2 - 2 класс Санкт-Петербург. Приморский район
Санкт-Петербург. Приморский район Абсолютные и относительные статистические показатели
Абсолютные и относительные статистические показатели Вычитание числа с переходом через десяток, вида 13-
Вычитание числа с переходом через десяток, вида 13- Сложение и вычитание десятков
Сложение и вычитание десятков 20231001_2._komplanarnye_vektory
20231001_2._komplanarnye_vektory Деление с остатком
Деление с остатком Степени и корни
Степени и корни Центральные и вписанные углы
Центральные и вписанные углы Окружность вписанная, описанная, вневписанная
Окружность вписанная, описанная, вневписанная Последовательность и образование чисел второго десятка
Последовательность и образование чисел второго десятка Равнобедренный треугольник. Геометрия 7 класс
Равнобедренный треугольник. Геометрия 7 класс Формулы двойного аргумента
Формулы двойного аргумента Анимашки для оформления презентаций в Microsoft Power Point. Сборник №3
Анимашки для оформления презентаций в Microsoft Power Point. Сборник №3 презентация Веселая неделя
презентация Веселая неделя Чётные и нечётные функции. Периодические функции
Чётные и нечётные функции. Периодические функции Математическая игра Поле чудес
Математическая игра Поле чудес Слагаемые. Сумма
Слагаемые. Сумма Гарфилд изучает дроби
Гарфилд изучает дроби Математическая разминка для 1 класса
Математическая разминка для 1 класса Прямоугольник и квадрат
Прямоугольник и квадрат Состав чисел в приделах 10. Страничка для любознательных
Состав чисел в приделах 10. Страничка для любознательных Зерттеу мәліметтерді негізгі статистикалық өңдеу әдістері
Зерттеу мәліметтерді негізгі статистикалық өңдеу әдістері Решение задач, масса одного предмета, количество, масса всех предметов
Решение задач, масса одного предмета, количество, масса всех предметов Алгоритм умножения. 4 класс
Алгоритм умножения. 4 класс