Слайд 2

Экстремум функции нескольких переменных.
Пусть функция z = f (x;y) определена в
некоторой области D и точка М0(x0,y0) ∈ D.
Точка М0 называется точкой максимума функции z = f (x;y), если для любой точки М(x,y), принадлежащей δ - окрестности точки М0 и такой, что М≠М0 выполняется неравенство f(М) < f(М0).
Точка М0 называется точкой минимума функции z = f (x;y), если для любой точки М(x,y), принадлежащей δ - окрестности точки М0 и такой, что М≠М0 выполняется неравенство f(М) > f(М0).
Следовательно, в точке максимума функция z = f(x;y) принимает значение наибольшее, а в точке минимума – наименьшее по сравнению с ее значениями во всех достаточно близких точках. Максимум и минимум функции называются ее экстремумами и обозначают max f(x,y) и min f(x,y).
Слайд 3

Теорема(необходимые условия существования экстремума).
Если дифференцируемая функция z = f(x;y) имеет в
точке М0(x0;y0) экстремум, то обе первые частные производные в этой точке равны нулю.
Доказательство.
Пусть в точке М0(x0;y0) функция z = f(x;y) имеет экстремум.
Положим у = у0 и рассмотрим функцию одного переменного х:
f(x,y0) = φ(x).
Очевидно, что точка х = х0 является точкой экстремума для функции φ(x) и поэтому производная от нее в точке х0 (если производная существует) должна обращаться в нуль: φ′(x0) = f′x(x0,y0)=0.
Аналогично, положив х=х0, и рассматривая функцию одного переменного у: f(x0,y) = ψ(y), получим, что в точке экстремума ψ′(y0) = f′y(x0,y0)=0 (согласно необходимому условию функции одной переменной).
Слайд 4

Критические точки функции двух переменных.
Точки, в которых выполняются необходимые условия
экстремума называются критическими или стационарными.
В критических точках (также как и для функции одной переменной) функция двух переменных z = f (x;y) может иметь экстремум, а может и не иметь.
Для нахождения экстремума функции необходимо каждую критическую точку дополнительно исследовать с помощью достаточного признака.
Слайд 5

Теорема (достаточные условия существования экстремума)
Слайд 6

Слайд 7

Слайд 8

Точка М называется внутренней точкой множества G, если существует δ
- окрестность точки М, целиком принадлежащая множеству G.
Точка М0 называется граничной точкой множества G, если в любой δ - окрестности точки М0 содержатся точки, как принадлежащие множеству G, так и не принадлежащие ему. Совокупность всех граничных точек множества G называется его границей Г.
Множество G называется открытой областью или областью, если все его точки – внутренние и любые две точки множества G (точки M и N рис.4) можно соединить непрерывной кривой, также лежащей внутри G.
Открытая область с присоединенной границей Г называется замкнутой областью.
Слайд 9

Область называется ограниченной, если она целиком содержится внутри круга (или шара)
достаточно большого радиуса.
Функция z = f(x;y) = f(М) называется непрерывной в открытой или замкнутой области, если она непрерывна в каждой точке этой области.
Если функция z = f(М) непрерывна в ограниченной замкнутой области, то она в этой области:
- имеет наибольшее и наименьшее значения;
- ограничена:│f(M)│≤ К (К - положительное число);
- принимает в этой области все значения, заключенные между наименьшими и наибольшими ее значениями.
Слайд 10

Наибольшее и наименьшее значения в замкнутой области.
Отметим, что кроме экстремальных значений
функции z = f(x;y) (так называемых локальных экстремумов) можно отыскивать наибольшее и наименьшее значения функции в замкнутой области (глобальный экстремум). При этом, например, наибольшее значение может не совпадать ни с одним из максимумов и достигаться на границе области.
Пусть z = f(x;y) определена и непрерывна в ограниченной замкнутой области D, тогда среди значений функции заведомо имеется наибольшее и наименьшее. Правило нахождения этих значений:
Найти все стационарные точки функции внутри области D и на ее границе и вычислить значения функции в них.
Сравнить все найденные значения функции и выбрать из них наибольшее M и наименьшее m.
Слайд 11

Слайд 12

Слайд 13

Касательная плоскость и нормаль к поверхности.
Слайд 14

Касательная плоскость и нормаль к поверхности.
Слайд 15

Касательная плоскость и нормаль к поверхности.
Слайд 16

Касательная плоскость и нормаль к поверхности.
Слайд 17

Касательная плоскость и нормаль к поверхности.
Слайд 18

Касательная плоскость и нормаль к поверхности.
Слайд 19

Касательная плоскость и нормаль к поверхности.
Слайд 20




















 Многоугольники, вписанные в окружность. Геометрия, 8 класс
Многоугольники, вписанные в окружность. Геометрия, 8 класс методическая разработка урока математики для 1 класса по программе Школа 21 века по теме Прибавление числа 7 по ФГОС
методическая разработка урока математики для 1 класса по программе Школа 21 века по теме Прибавление числа 7 по ФГОС Логические задачи. Логические операции
Логические задачи. Логические операции Действия с дробями. 6 класс
Действия с дробями. 6 класс Разбор логарифмических уравнений
Разбор логарифмических уравнений Активизация мыслительной деятельности учащихся на уроках математики
Активизация мыслительной деятельности учащихся на уроках математики Интегрированный урок во 2 классе по английскому языку и математике
Интегрированный урок во 2 классе по английскому языку и математике Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация)
Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация) Загальні характеристики ППП
Загальні характеристики ППП Квадратные уравнения
Квадратные уравнения Переместительное свойство умножения
Переместительное свойство умножения Построение правильных многоугольников
Построение правильных многоугольников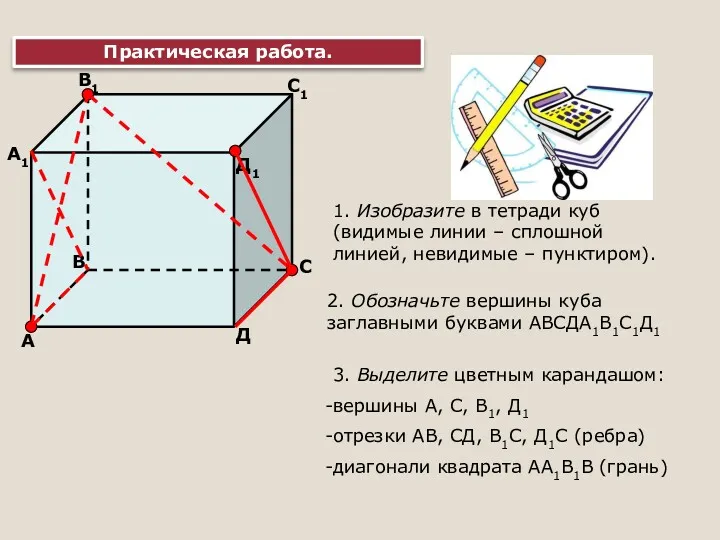 Решение задач по стереометрии
Решение задач по стереометрии Понятие, задачи корреляционно-регрессионного анализа и моделирования
Понятие, задачи корреляционно-регрессионного анализа и моделирования Умножение десятичных дробей
Умножение десятичных дробей Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Иррациональные уравнения
Иррациональные уравнения Формирование познавательных ууд на уроках математики в начальной школе.
Формирование познавательных ууд на уроках математики в начальной школе. Теорема Пифагора
Теорема Пифагора 7 санына көбейту және бөлу кестесі
7 санына көбейту және бөлу кестесі Количественные характеристики случайных переменных
Количественные характеристики случайных переменных Треугольник. Повторение
Треугольник. Повторение Решение задач на движение – закрепление.
Решение задач на движение – закрепление. Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе)
Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе) Прямоугольный параллелепипед. Прямоугольный параллелепипед в нашей жизни
Прямоугольный параллелепипед. Прямоугольный параллелепипед в нашей жизни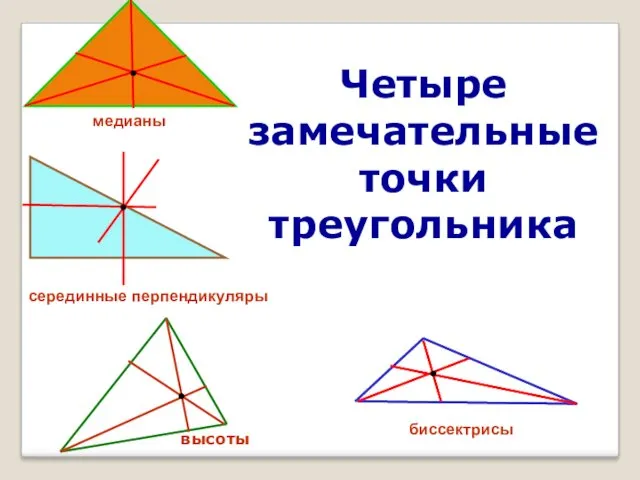 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Статистика бюджета. Экономические модели
Статистика бюджета. Экономические модели Производная показательной функции
Производная показательной функции