Слайд 2

§1. Понятие функции нескольких переменных
Если каждой упорядоченной паре чисел (x;y) из
некоторого числового множества
поставлено в соответствие согласно некоторому правилу f число z из множества Z, то говорят, что на множестве
D задана функция двух переменных
Слайд 3

При этом переменные x и y называются независимыми переменными (или
аргументами).
Множество
называется областью определения, а множество
– множеством значений функции.
Областью определения может быть вся плоскость OXY, или ее часть, ограниченная некоторыми линиями.
Слайд 4

Линию, ограничивающую область, называют границей области.
Точки области, не лежащие на
границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой.
Область с присоединенной к ней границей называется замкнутой, обозначается D .
Примером замкнутой области является круг с окружностью.
Слайд 5

Значение функции в точке обозначают и называют частным значением функции.
Пример.
Найти значение
функции
в точке
Решение.
Слайд 6

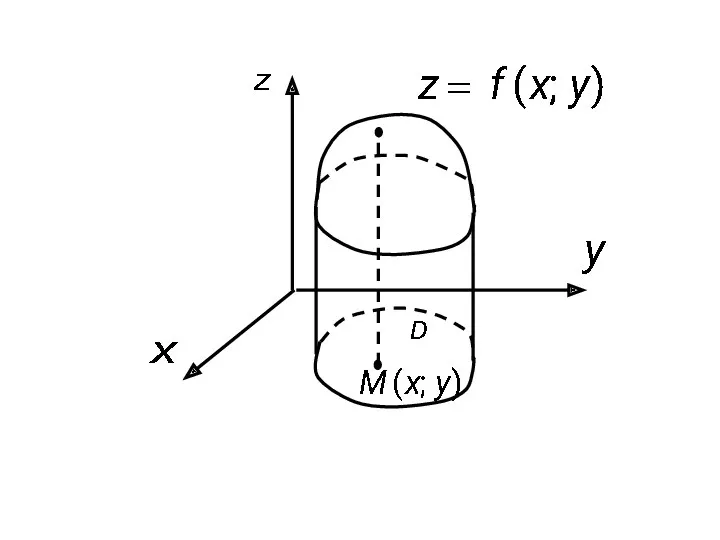
Графиком функции
называется поверхность, образованная множеством точек пространства с координатами
для всех
Слайд 7
Слайд 8

Пример
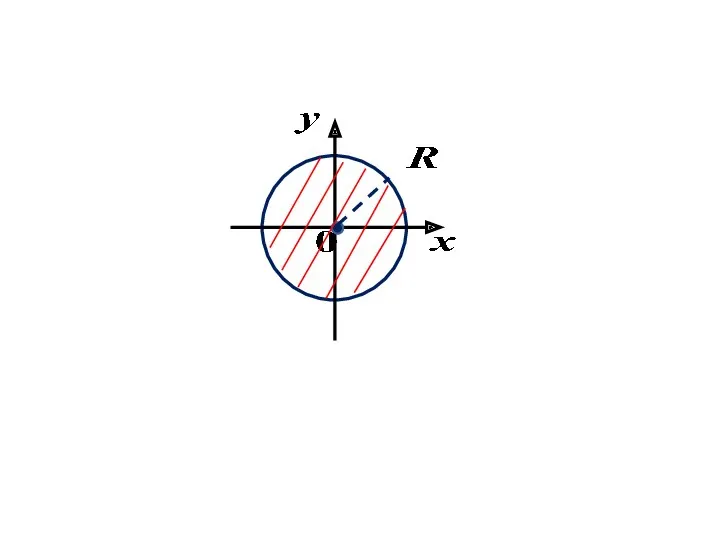
Найти область определения функции:
Решение.
Построим линию
Это окружность с центром в точке
и
радиусом
Слайд 9
Слайд 10

Функция двух переменных, как и функция одной переменной, может быть задана
разными способами:
- таблицей,
- аналитически,
- графиком.
Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.
Слайд 11

Величина u называется функцией n переменных если каждой совокупности переменных
из некоторой области n-мерного пространства соответствует определенное значение u, что символически записывается
Слайд 12

Линии уровня
Линией уровня функции называется множество всех точек плоскости OXY
, в которых функция z принимает постоянное значение, т. е. где C – постоянная.
Число C в этом случае называется уровнем.
Слайд 13

Многие примеры линий уровня хорошо известны и привычны.
Например, параллели и
меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм — линий уровня температуры.
Построение линий уровня оказывается существенно более легкой задачей, чем построение графиков самих функций.
Слайд 14

§2. Предел и непрерывность функции 2-х переменных
ОПР. -окрестностью точки
называется множество
всех точек
плоскости, координаты которых удовлетворяют неравенству
Т.е. -окрестность точки – это круг радиуса , с центром в точке
Слайд 15

Пусть функция определена в некоторой окрестности точки кроме быть может самой
точки.
Опр. Число A называется пределом функции при и , если для любого , найдется положительное число , такое, что для всех и , удовлетворяющих неравенству
выполняется неравенство
Слайд 16

Записывают
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной
переменной.
Слайд 17

Опр. Функция называется непрерывной в точке , если она:
1) определена
в этой точке и некоторой ее окрестности;
2) имеет конечный предел
3) этот предел равен значению функции z в точке
Слайд 18

Геометрический смысл непрерывности очевиден: график в точке представляет собой сплошную, нерасслаивающуюся
поверхность.
ОПР. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Слайд 19

§3. Частные производные ФНП
Частным приращением функции
по независимой переменной x, соответствующим
приращению переменной x, называется разность
Слайд 20

Частным приращением функции
по независимой переменной y, соответствующим приращению переменной
y, называется разность
Полным приращением функции соответствующим приращениям аргументов и называется разность
Слайд 21

Частной производной первого порядка функции нескольких переменных по одной из этих
переменных называется предел отношения соответствующего частного приращения функции к приращению данной переменной, когда последнее стремится к нулю.
Слайд 22

Для функции двух переменных
по определению частная производная по x равна
частная
производная по y равна
Слайд 23

При нахождении частной производной пользуются правилами дифференцирования функции одной переменной, считая
все другие аргументы постоянными.
Слайд 24

Пример
Найти частные производные первого порядка
Решение. Считая y постоянной и дифференцируя данную
функцию как функцию переменной x, находим частную производную по x:
Слайд 25
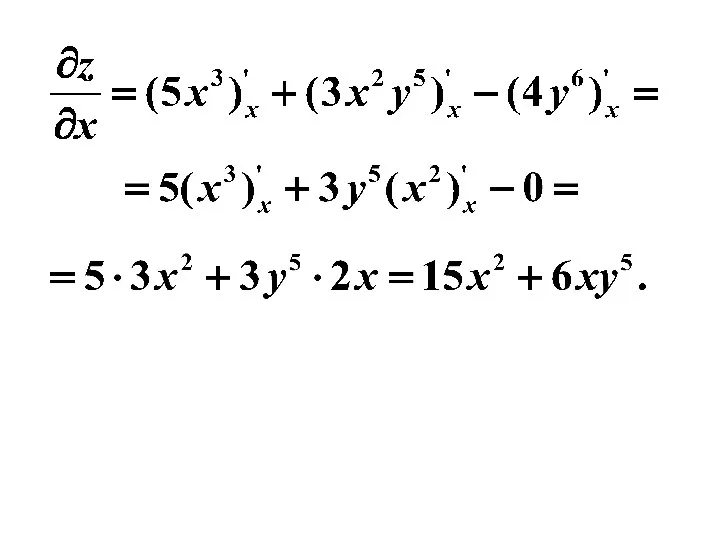
Слайд 26

Считая x постоянной и дифференцируя z как функцию переменной y, находим
частную производную по y:
Слайд 27

Частные производные второго порядка
Частными производными второго порядка функции называются частные
производные, если они существуют, от ее частных производных первого порядка.
Слайд 28

Обозначения частных производных второго порядка:
Слайд 29

Аналогично определяются и обозначаются частные производные третьего и высших порядков.
Частные производные называются смешанными производными.
Если функция дважды дифференци-руема в некоторой точке, то в этой точке смешанные производные равны.
Слайд 30

§4. Полный дифференциал ФНП
Пусть функция определена в некоторой окрестности точки составим
полное приращение функции в точке
Слайд 31

Полный дифференциал функции
можно найти по формуле
Слайд 32

Пример. Найти полный дифференциал функции
Решение.























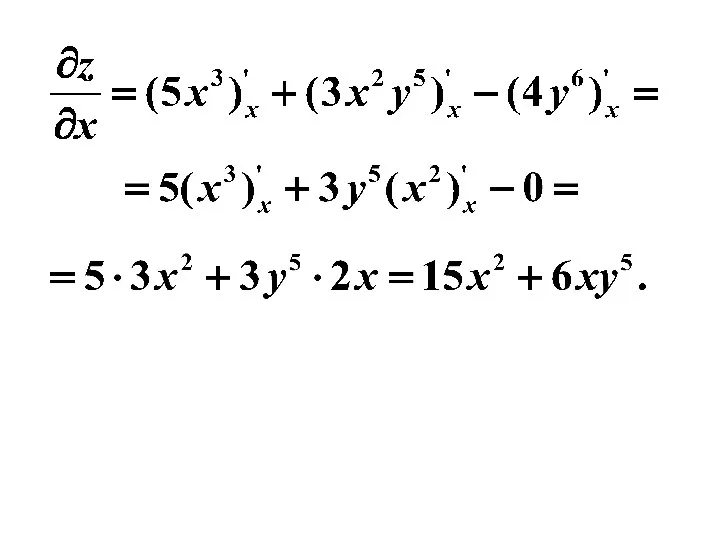







 Проверка статистических гипотез
Проверка статистических гипотез Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе
Числа и вычисления. Подготовка к ГИА. К уроку математики в 9 классе Соотношение единиц площади.
Соотношение единиц площади. Умножение многочлена на многочлен
Умножение многочлена на многочлен Статистика знает всё
Статистика знает всё Экспресс-тренинг по подготовке к ЕГЭ по математике
Экспресс-тренинг по подготовке к ЕГЭ по математике Цилиндр. 9 класс
Цилиндр. 9 класс Комбинаторное правило умножения. Урок №2
Комбинаторное правило умножения. Урок №2 Масштаб. Расчет и изображение чертежей в масштабе
Масштаб. Расчет и изображение чертежей в масштабе Книга сказок
Книга сказок Похідна складеної функції
Похідна складеної функції Линейная алгебра. Лекция 4
Линейная алгебра. Лекция 4 Бином Ньютона и тругольник Паскаля
Бином Ньютона и тругольник Паскаля Конспект и презентация к уроку математики : Точки на осях координат.
Конспект и презентация к уроку математики : Точки на осях координат. Устный счет
Устный счет Решение сложных уравнений (4 класс)
Решение сложных уравнений (4 класс) Состав чисел первого десятка.
Состав чисел первого десятка. Умножение и его свойства
Умножение и его свойства Прямоугольный параллелепипед
Прямоугольный параллелепипед Квадратичная функция и ее график. 9 класс
Квадратичная функция и ее график. 9 класс Урок Угол. Виды углов 2 класс
Урок Угол. Виды углов 2 класс Арифметическая и геометрическая прогрессии. Обобщающий урок
Арифметическая и геометрическая прогрессии. Обобщающий урок Математический тренажер по теме Сложение и вычитание в пределах 20
Математический тренажер по теме Сложение и вычитание в пределах 20 Симметрия в природе
Симметрия в природе Теория вероятности. Основные понятия
Теория вероятности. Основные понятия Множества. Деревья. (Лекция 6)
Множества. Деревья. (Лекция 6) Викторина по математике
Викторина по математике открытый урок
открытый урок