Содержание
- 2. Основные вопросы: Понятие предела функции. Основные теоремы о пределах функций (суммы, произведения и частного). Методы вычисления
- 3. ПРЕДЕЛ ФУНКЦИИ Предел – одно из основных понятий математического анализа. Понятие предела использовалось еще Ньютоном во
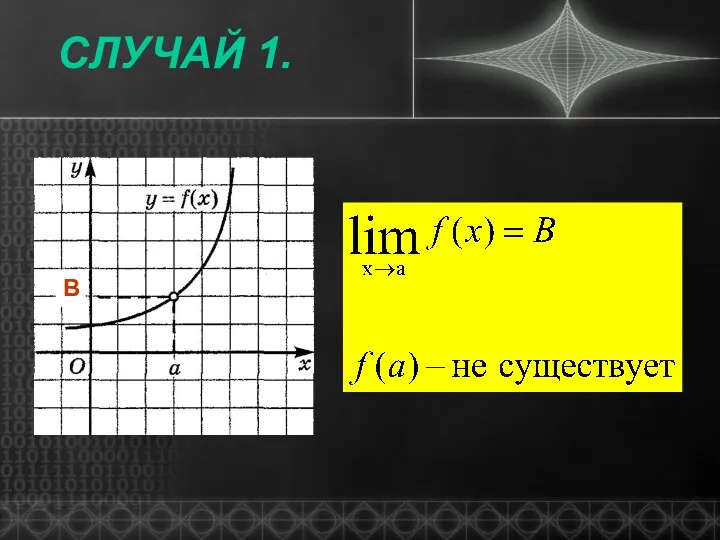
- 4. СЛУЧАЙ 1. В
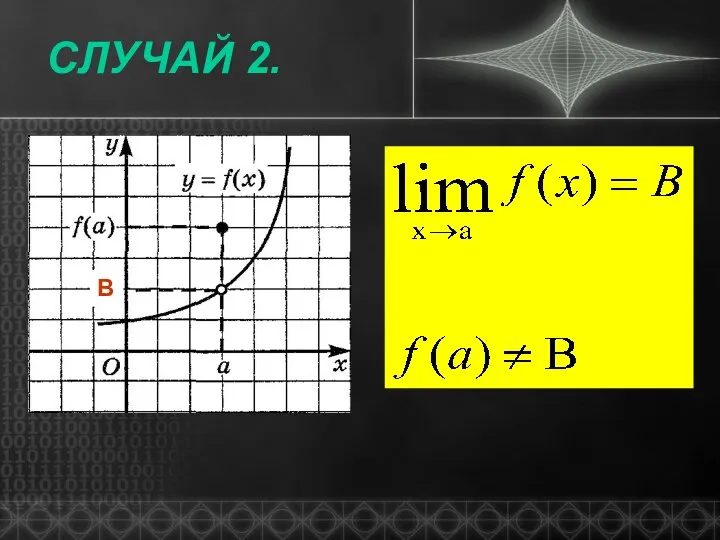
- 5. СЛУЧАЙ 2. В
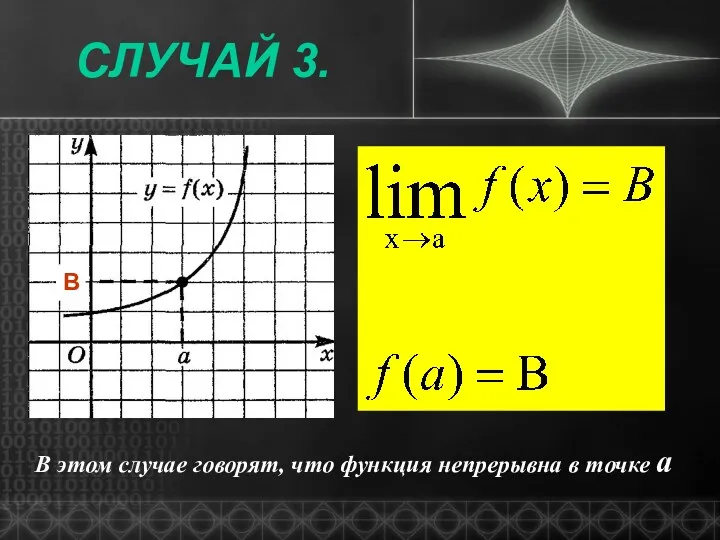
- 6. СЛУЧАЙ 3. В В этом случае говорят, что функция непрерывна в точке а
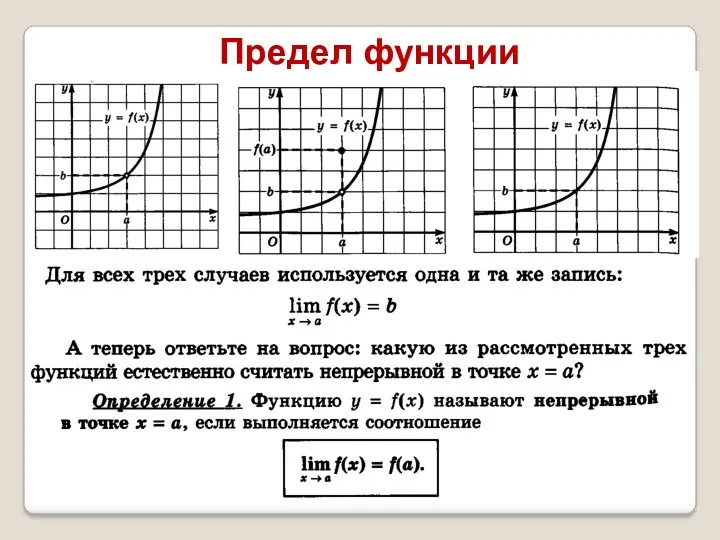
- 7. Предел функции
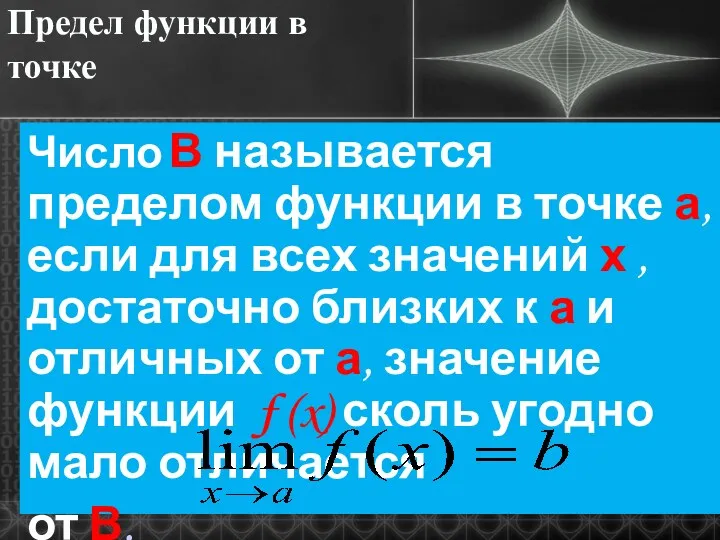
- 8. Предел функции в точке Число В называется пределом функции в точке а, если для всех значений
- 9. Теорема 1. Предел суммы (разности) 2-х функций равен сумме (разности) их пределов, если последние существуют:
- 10. Теорема 2. Предел константы равен самой этой константе.
- 11. Теорема 3. Предел произведения 2-х функций равен произведению их пределов, если последние существуют:
- 12. Теорема 4. Предел отношения 2-х функций равен отношению) их пределов, если последние существуют и предел знаменателя
- 13. Теорема 5. Постоянный множитель можно выносить за знак предела
- 14. Теорема 6. Предел степени переменного равен той же степени предела основания:
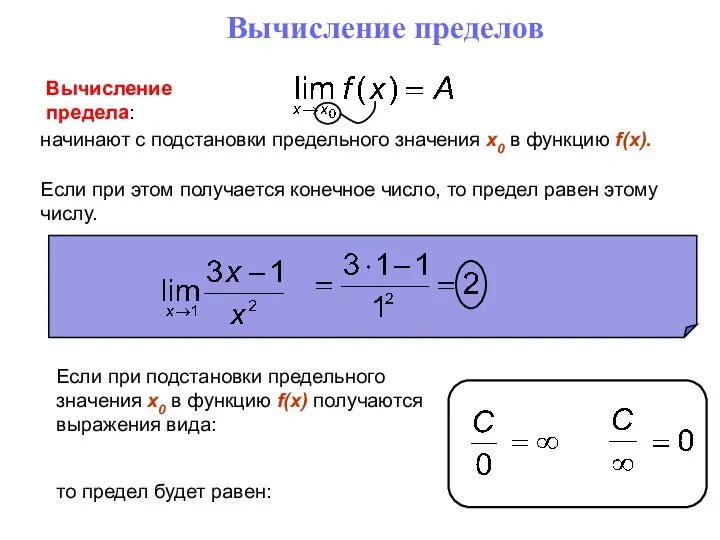
- 15. Вычисление пределов Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при этом
- 16. Вычислить пределы:
- 17. Примеры
- 18. Последовательности, пределы.
- 19. Вычисление пределов Часто при подстановке предельного значения x0 в функцию f(x) получаются выражения следующих видов: Эти
- 20. Методы вычисления пределов на неопределенность Раскрыть соответствующую неопределенность- это значит найти предел (если он существует) соответствующего
- 21. В большинстве случаев, чтобы раскрыть неопределенность вида , достаточно числитель и знаменатель дроби разделить на множители,
- 22. Пример №1: Разложим числитель и знаменатель на множители:
- 23. Пример № 2:
- 24. Чтобы раскрыть неопределенность данного вида, зависящую от иррациональности, достаточно перевести иррациональность (или иррациональности) из числителя в
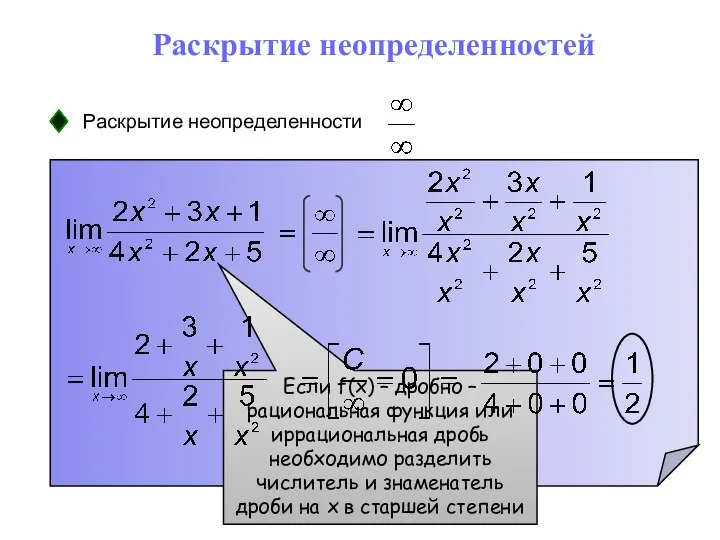
- 25. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция, необходимо разложить на множители числитель
- 27. Основные правила раскрытия неопределенностей вида В процессе вычисления пределов функций могут встретиться разные случаи:
- 28. Прямую подстановку использовать нельзя в тех случаях, когда мы не можем вычислить значение элементарной функции, стоящей
- 29. Бывают неопределённости вида Чтобы раскрыть неопределенность вида , надо числитель и знаменатель дроби почленно разделить на
- 30. Раскрытие неопределенностей Раскрытие неопределенности Если f(x) – дробно – рациональная функция или иррациональная дробь необходимо разделить
- 31. Замечание: если в числителе и знаменателе многочлены одной степени, то предел равен отношению коэффициентов при старших
- 32. Например:
- 33. Раскрытие неопределенностей Раскрытие неопределенности Умножим и разделим функцию на сопряженное выражение.
- 34. Упражнения:
- 35. Упражнения:
- 36. Упражнения:
- 38. Скачать презентацию




























 Модели числового неравенства. Числовые промежутки
Модели числового неравенства. Числовые промежутки Специфика преподавания математики в рамках УМК А.Г. Модковича. 10 - 11 классы
Специфика преподавания математики в рамках УМК А.Г. Модковича. 10 - 11 классы Математический диктант
Математический диктант Числовые неравенства и их свойства
Числовые неравенства и их свойства Длина ломаной
Длина ломаной Умники и умницы. Матиматека
Умники и умницы. Матиматека Графическое решение уравнений с двумя переменными
Графическое решение уравнений с двумя переменными Использование свойств функций при решении уравнений и неравенств
Использование свойств функций при решении уравнений и неравенств Вписанная и описанная окружности
Вписанная и описанная окружности Теорема Менелая
Теорема Менелая Действия с дробями
Действия с дробями Название чисел в записи действий. Закрепление.
Название чисел в записи действий. Закрепление. Геометрические тела
Геометрические тела Контурные интегралы функций комплексного переменного (ФКП)
Контурные интегралы функций комплексного переменного (ФКП) Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменными Математика - царица наук
Математика - царица наук Презентация к уроку математики во 2 классе по теме Периметр
Презентация к уроку математики во 2 классе по теме Периметр Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Возрастание и убывание функции. Применение производной к исследованию функций
Возрастание и убывание функции. Применение производной к исследованию функций Математика. Приклади. Диск
Математика. Приклади. Диск Графики тригонометрических функций и их свойства
Графики тригонометрических функций и их свойства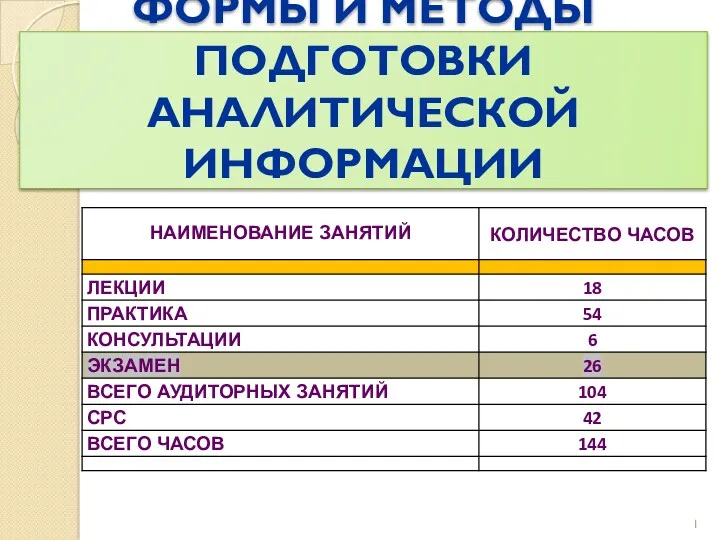 Формы и методы подготовки аналитической информации
Формы и методы подготовки аналитической информации Векторы в жизни
Векторы в жизни Математика в профессии электрика
Математика в профессии электрика Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра
Цилиндр. Цилиндрическая поверхность. Площадь полной поверхности и объем цилиндра Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Призма
Призма Время. Сутки
Время. Сутки