Содержание
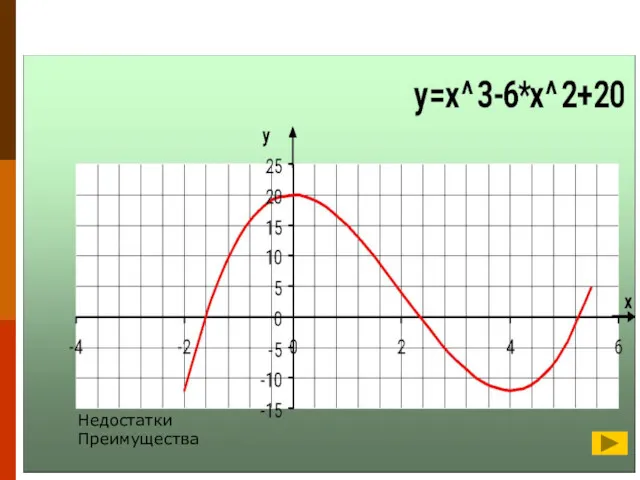
- 2. Пусть дано уравнение x^3-6*x^2+20 =0
- 3. Недостатки Преимущества
- 4. Недостатки Можно найти корни уравнения в некотором ограниченном интервале, т.к. чертеж неизбежно ограничен Для получения корней
- 5. Преимущества Позволяет найти корни с точностью, достаточной для решения практических задач Простота Доступность Наглядность
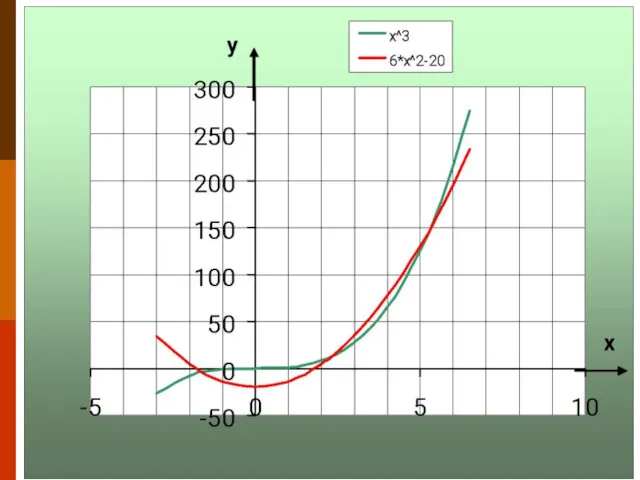
- 6. Применяют запись уравнения, при которой используются функции, графики которых хорошо известны φ(x) = g(x) x^3 =
- 8. Задача об отыскании всех корней уравнения Сделан чертеж для ограниченного промежутка На чертеже графики функций y=φ(x)
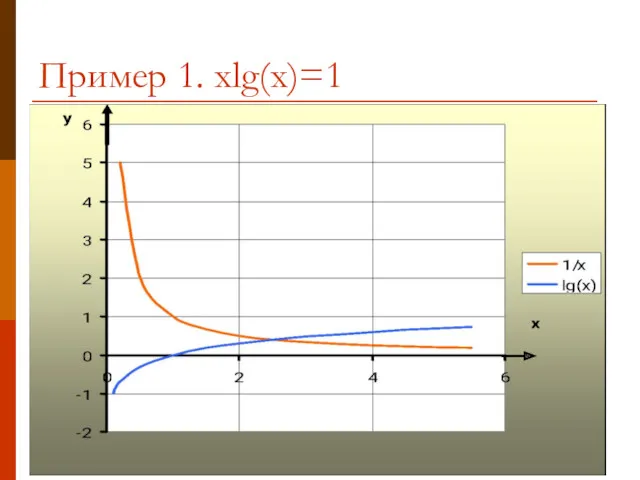
- 9. Пример 1. xlg(x)=1
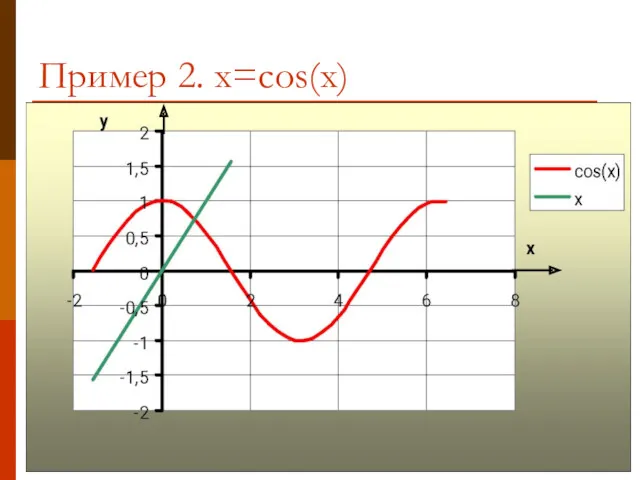
- 10. Пример 2. x=cos(x)
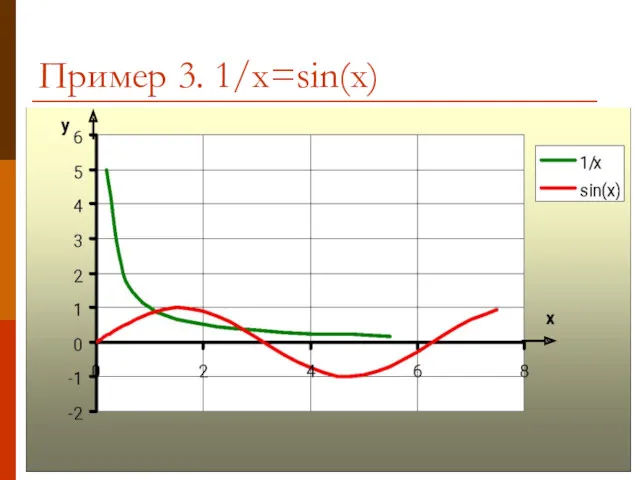
- 11. Пример 3. 1/x=sin(x)
- 12. Последовательность действий Представить уравнение в виде φ(x) = g(x) так, чтобы графики функций y=φ(x) и y=g(x)
- 13. Пример оформления задания по графическому решению уравнения в электронной таблице
- 15. Отделение корней уравнения Для получения значения корня с любой степенью точности применяются численные методы Нахождение приближенных
- 16. Отделение корней. Определение Говорят, что корень уравнения отделен на отрезке [a;b], если этот корень содержится в
- 17. Отделение корней Графически Аналитически (основываясь на свойствах функции).
- 18. Теорема Если функция f(x) непрерывна на отрезке [a;b], принимает на концах отрезка значения разных знаков, а
- 19. Пример Отделим корни уравнения x^3-6*x^2+20 =0 1. Графически 2. Аналитически
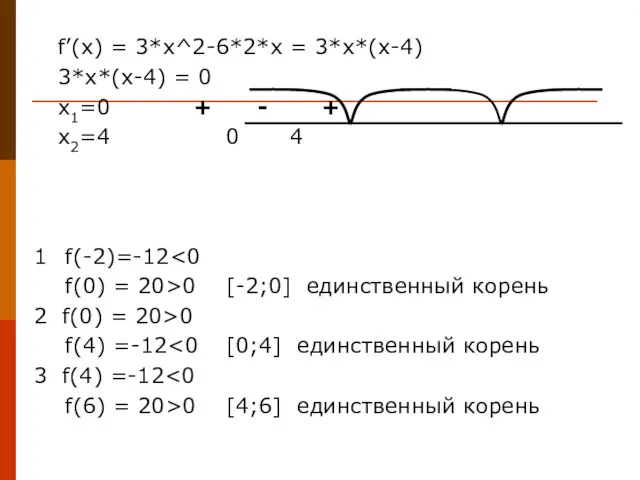
- 20. f’(x) = 3*x^2-6*2*x = 3*x*(x-4) 3*x*(x-4) = 0 x1=0 + - + x2=4 0 4 1
- 21. Полное отделение корней: (-∞;-2] нет корней (-2;0] один корень (0;4] один корень (4;6] один корень (6;
- 22. Уточнение корней Пусть дано уравнение f(x) = 0. Требуется найти корень с точностью Пусть этот корень
- 24. Скачать презентацию











![Теорема Если функция f(x) непрерывна на отрезке [a;b], принимает на](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/127034/slide-17.jpg)

![Полное отделение корней: (-∞;-2] нет корней (-2;0] один корень (0;4]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/127034/slide-20.jpg)

 Сравнение фигур. 7 класс
Сравнение фигур. 7 класс Биссектриса угла. 5 класс
Биссектриса угла. 5 класс Письменое сложение и вычание многозначных чисел
Письменое сложение и вычание многозначных чисел Презентация к уроку Площадь фигур Полякова 2 класс
Презентация к уроку Площадь фигур Полякова 2 класс Презентация Учимся правильно писать цифры. 1 класс
Презентация Учимся правильно писать цифры. 1 класс Тест Свойства четырехугольников
Тест Свойства четырехугольников Презентация для устного счета 1класс
Презентация для устного счета 1класс Конспект занятия в средней группе по ФЭМП в виде презентации
Конспект занятия в средней группе по ФЭМП в виде презентации Блочная система обучения математике
Блочная система обучения математике Работа с матрицами и решение систем линейных алгебраических уравнений
Работа с матрицами и решение систем линейных алгебраических уравнений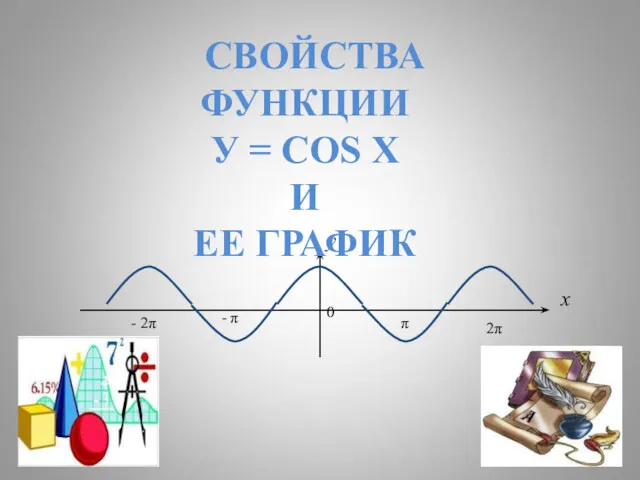 Свойства функции y=cos-x и ее график
Свойства функции y=cos-x и ее график Умножение вектора на число
Умножение вектора на число Урок математики 4 класс Умножение чисел, оканчивающихся нулями
Урок математики 4 класс Умножение чисел, оканчивающихся нулями Формула Тейлора
Формула Тейлора Длина окружности
Длина окружности Презентация Решение задач
Презентация Решение задач Предел функции
Предел функции Вставь пропущенные цифры
Вставь пропущенные цифры Экономические задачи
Экономические задачи Методы и алгоритмы цифровой обработки сигналов на базе MATLAB. Адаптивные фильтры
Методы и алгоритмы цифровой обработки сигналов на базе MATLAB. Адаптивные фильтры Роль математики в современных профессиях
Роль математики в современных профессиях Решение задач на применение признаков равенства треугольников
Решение задач на применение признаков равенства треугольников Презентация по математике на тему : Задачи
Презентация по математике на тему : Задачи Тела вращения
Тела вращения Типовые классы детерминированных аналитических моделей
Типовые классы детерминированных аналитических моделей Правильные многогранники
Правильные многогранники Математика вокруг нас
Математика вокруг нас Кто хочет получить 5? Игра. Действия с десятичными дробями
Кто хочет получить 5? Игра. Действия с десятичными дробями