Содержание
- 2. Граф – наглядное представление конечного антирефлексивного симметричного отношения Граф – конечное множество V, называемое множеством вершин,
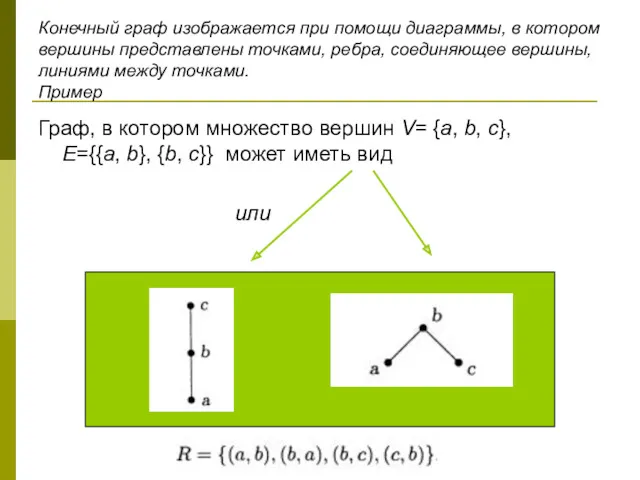
- 3. Конечный граф изображается при помощи диаграммы, в котором вершины представлены точками, ребра, соединяющее вершины, линиями между
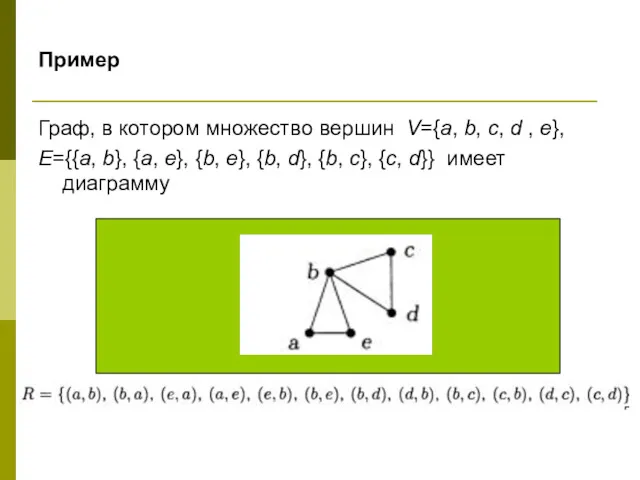
- 4. Пример Граф, в котором множество вершин V={a, b, c, d , e}, Е={{a, b}, {a, e},
- 5. Определения Ориентированный граф, или орграф G состоит из множества V вершин и отношения E на V,
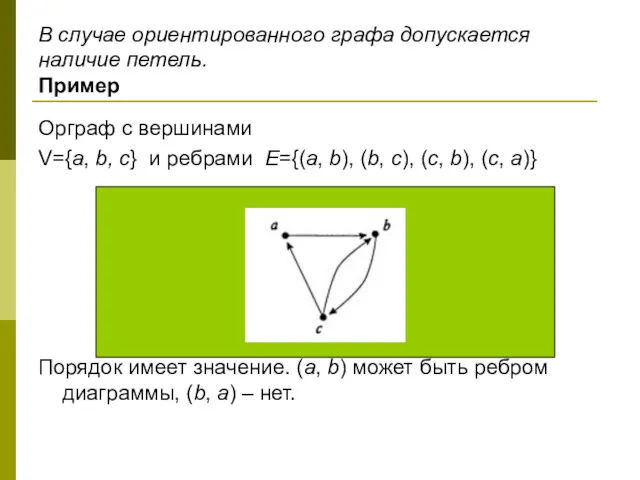
- 6. В случае ориентированного графа допускается наличие петель. Пример Орграф с вершинами V={a, b, c} и ребрами
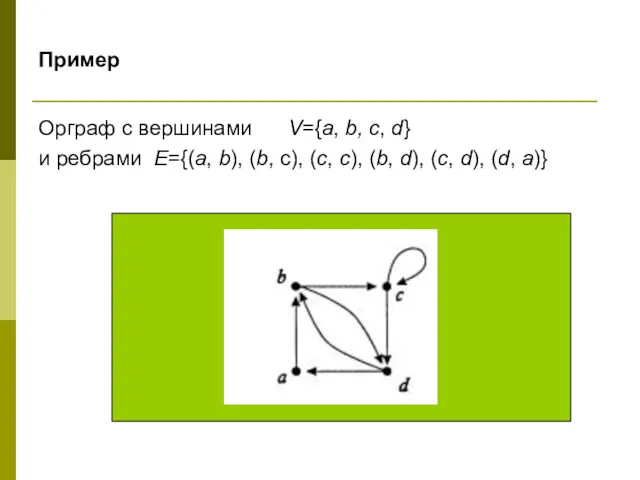
- 7. Пример Орграф с вершинами V={a, b, c, d} и ребрами E={(a, b), (b, c), (c, c),
- 8. Определение Отношение R на А есть отношение частичного порядка, если оно рефлексивно, симметрично и транзитивно. Если
- 9. Пример (*) Пусть С = {1, 2, 3}, Х – множество всех подмножеств множества С: Определим
- 10. Пример Пусть S – множество действительных чисел, R1 – отношение, определенное условием (x, y) ∈ R1,
- 11. Определение Два элемента a и b ЧУ-множества (S, ≤) сравнимы, если a ≤ b или b
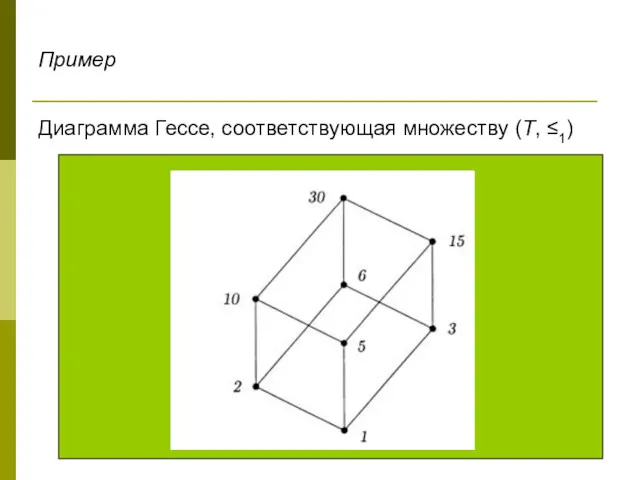
- 12. Примеры Пусть Т – множество положительных делителей числа 30 и ≤1 есть отношение m ≤1 n,
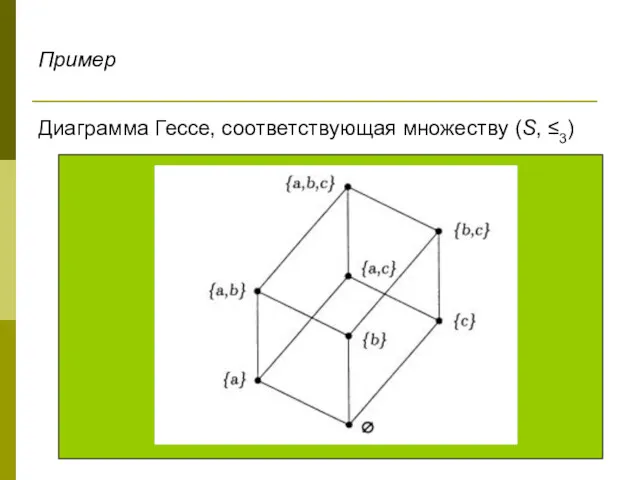
- 13. Пример Пусть S – множество всех подмножеств множества {a,b,c} ≤3 есть отношение частичного порядка в примере
- 14. Диаграммы Гессе Для изображения ЧУ-множеств. Для заданного ЧУ-множества (А, ≤2) диаграмма Гессе состоит из совокупности точек
- 15. Диаграмма Гессе, соответствующая множеству (Т, ≤1) Пример
- 16. Диаграмма Гессе, соответствующая множеству (S, ≤3) Пример
- 17. Матрицы инцидентности и смежности Задание любой из этих матриц дает возможность восстановить граф
- 18. Пусть G - граф. Пусть В – матрица, строки которой обозначены вершинами графа, а столбцы обозначены
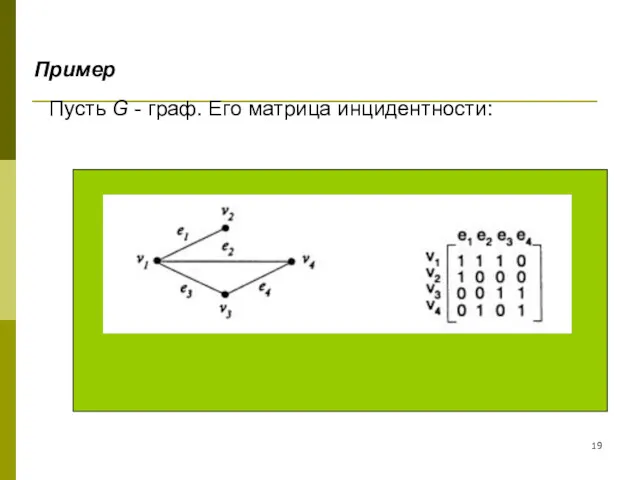
- 19. Пусть G - граф. Его матрица инцидентности: Пример
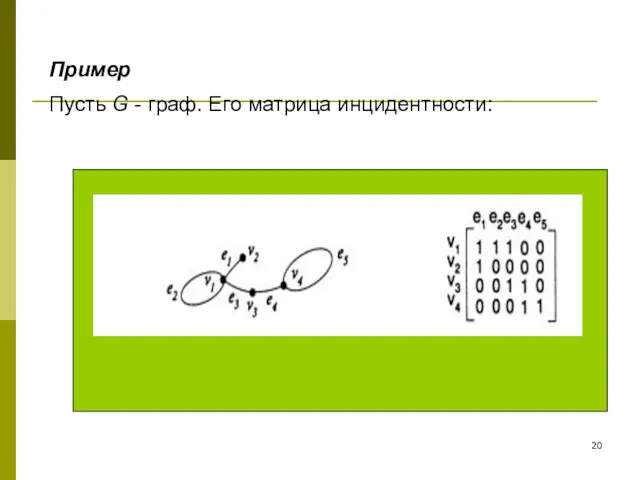
- 20. Пусть G - граф. Его матрица инцидентности: Пример
- 21. Пусть G – граф (ориентированный граф). Пусть В – матрица, строки которой обозначены вершинами графа и
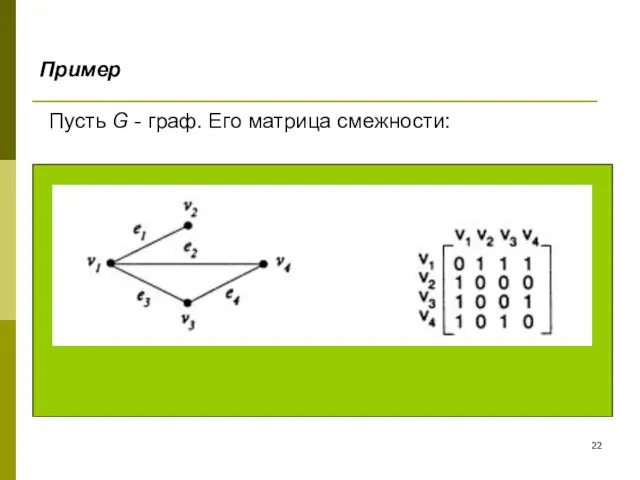
- 22. Пусть G - граф. Его матрица смежности: Пример
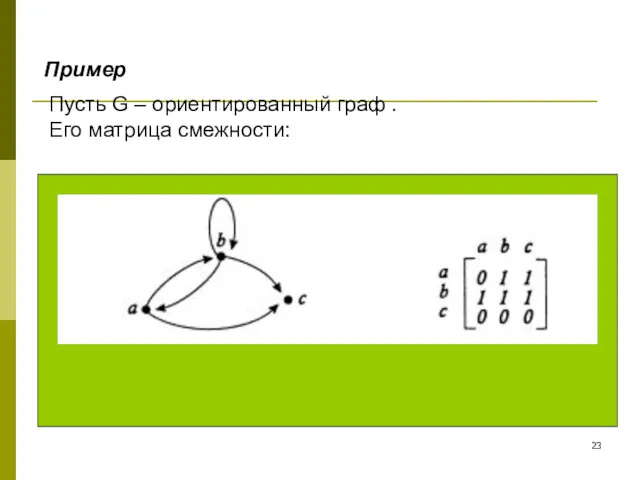
- 23. Пусть G – ориентированный граф . Его матрица смежности: Пример
- 24. Матрица смежности для ориентированного графа, у которого четыре и восемь ребер : Пример
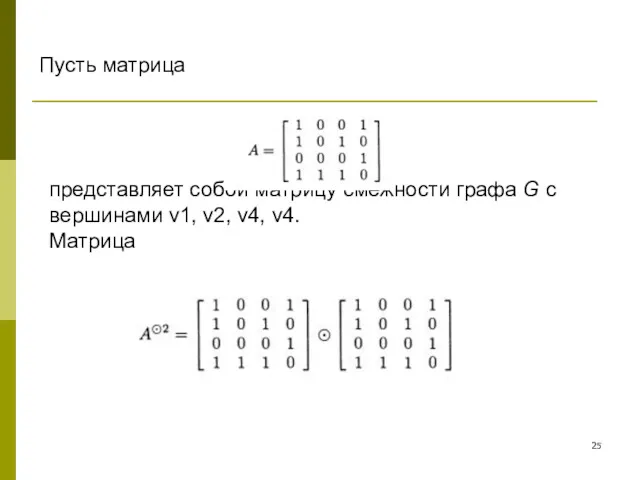
- 25. представляет собой матрицу смежности графа G с вершинами v1, v2, v4, v4. Матрица Пусть матрица
- 26. представляет собой матрицу смежности графа G с вершинами v1, v2, v4, v4. Пусть матрица
- 27. Пусть G – (ориентированный) граф с вершинами v1, v2, v3, …, vn и матрицей смежности А.
- 28. Алгебраические свойства графов
- 29. Определение. Функция f из графа G(V, E) в граф G'(V ', E ') называется гомоморфизмом из
- 30. Теорема. Если функция f – гомоморфизм из G в G' , то f(G) - подграф (f(V),
- 31. Определение. Гомоморфизм f :G → G' , является изоморфизмом, если f :V → V' и f
- 32. Определение. Если граф G(V, E) содержит ребро e={v1, v2} и граф G'(V ', E ') получен
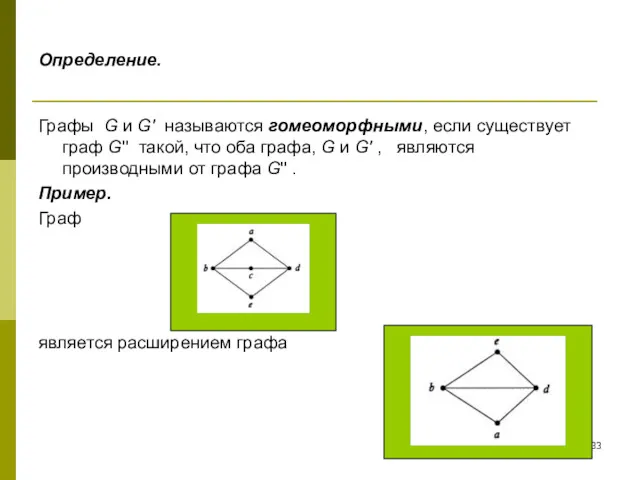
- 33. Определение. Графы G и G' называются гомеоморфными, если существует граф G'' такой, что оба графа, G
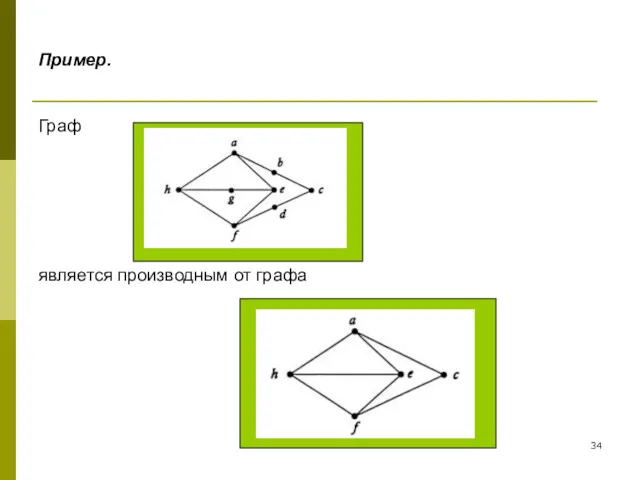
- 34. Пример. Граф является производным от графа
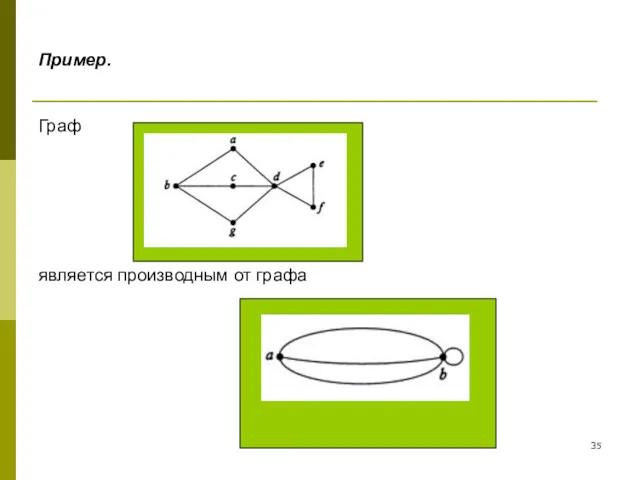
- 35. Пример. Граф является производным от графа
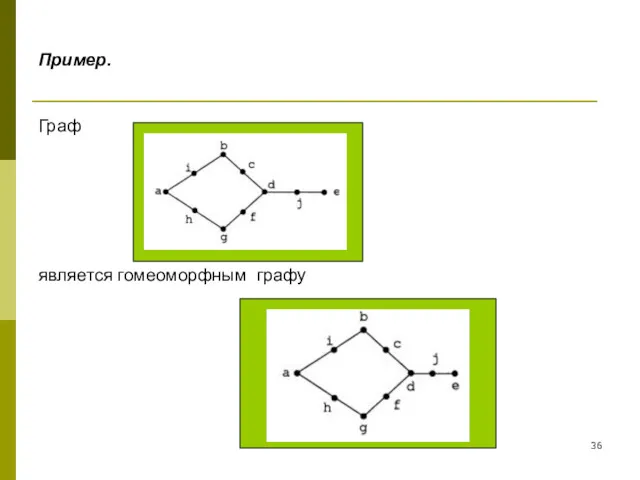
- 36. Пример. Граф является гомеоморфным графу
- 37. Теорема. Если графы G и G' – гомеоморфны, то у них одинаковое количество вершин нечетной степени.
- 38. Определение. Пусть G(V, E) - граф и G1 , G2 , G3 , …, Gn -
- 39. Определение. Пусть G(V, E) - граф и G1 , G2 , G3 , …, Gn -
- 40. Определение. Пусть G(V, E) - граф G1 , G2 , G3 , …, Gn - подграфы
- 41. Определение. Пусть G(V, E) - граф. Дополнением графа G называется граф такой, что для всех вершин
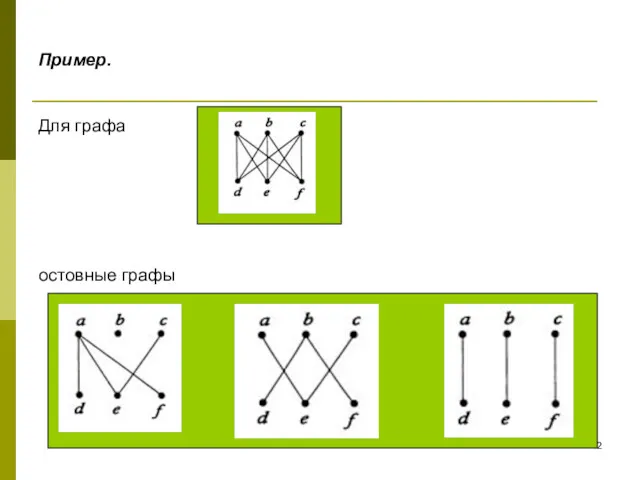
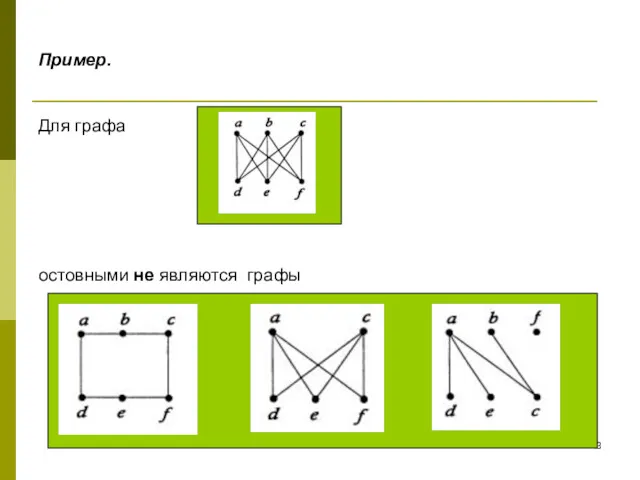
- 42. Пример. Для графа остовные графы
- 43. Пример. Для графа остовными не являются графы
- 44. Определение. Дерево называется остовным деревом графа G, если оно является остовным графом графа G. Теорема. Если
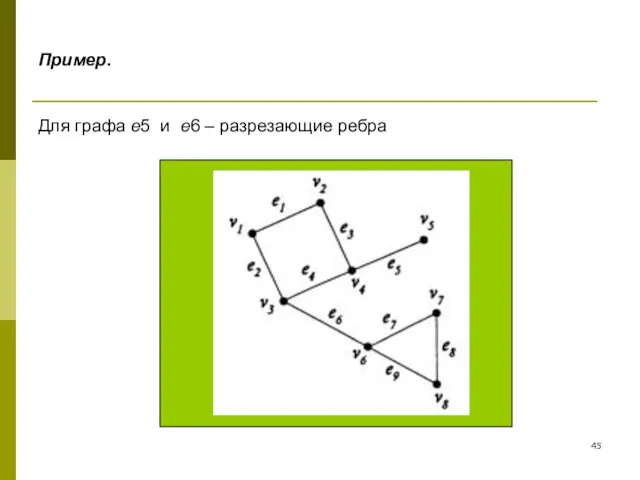
- 45. Пример. Для графа e5 и e6 – разрезающие ребра
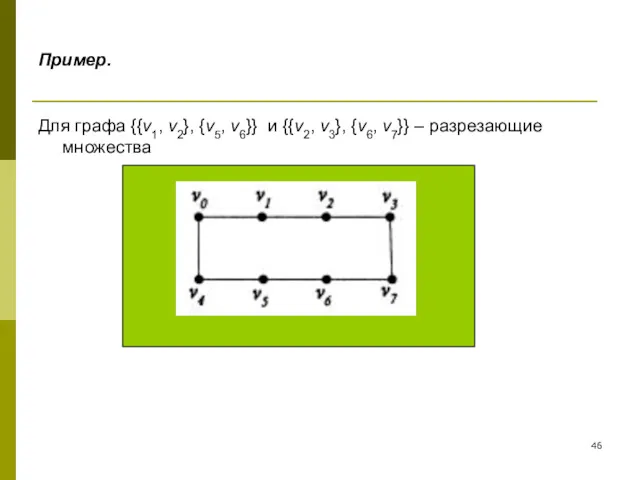
- 46. Пример. Для графа {{v1, v2}, {v5, v6}} и {{v2, v3}, {v6, v7}} – разрезающие множества
- 47. Теорема. Если T(V, E ') - остовное дерево графа G(V, E) и С – разрезающее множество
- 48. Задача Сколько городов лишится связи, если коммутационная сеть выйдет из строя в определенном городе (вершине графа).
- 49. Теорема Вершина a графа G=(V, E) является точкой сочленения тогда и только тогда, когда существуют различные
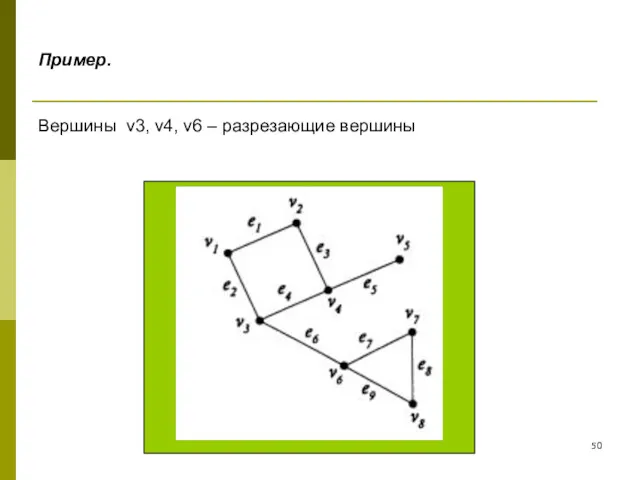
- 50. Пример. Вершины v3, v4, v6 – разрезающие вершины
- 51. Теорема Для связного графа G=(V, E) определим отношение R на E: e1 R e2 , если
- 52. Теорема. Если компонента двусвязности Gi =(Vi, Ei ) состоит из единственного ребра ei , то ei
- 53. Теорема. Вершина a является точкой сочленения тогда и только тогда, когда для некоторого i ≠ j
- 55. Скачать презентацию
































 Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Презентация Числа в загадках
Презентация Числа в загадках Числовые и буквенные выражения (4 класс)
Числовые и буквенные выражения (4 класс) Признаки равенства прямоугольных треугольников (тренажер)
Признаки равенства прямоугольных треугольников (тренажер)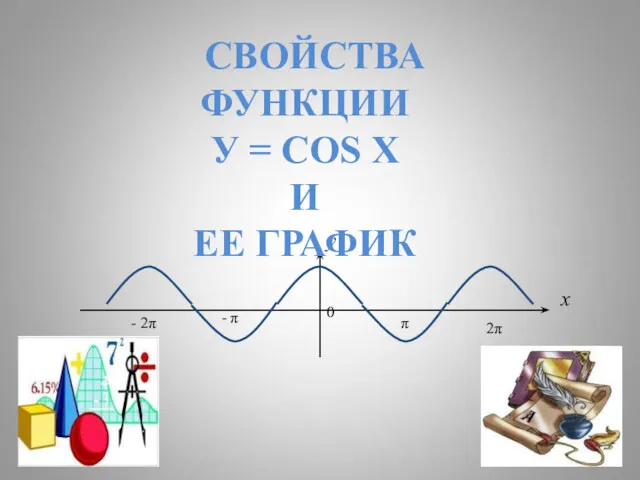 Свойства функции y=cos-x и ее график
Свойства функции y=cos-x и ее график Двугранный угол
Двугранный угол Умножение суммы на число
Умножение суммы на число Презентация к уроку математики 3 класс по теме Закрепление табличного умножения и деления. Диск
Презентация к уроку математики 3 класс по теме Закрепление табличного умножения и деления. Диск Взаимное расположение фигур на плоскости.
Взаимное расположение фигур на плоскости. Координаты на плоскости
Координаты на плоскости 6 ступень. Математика. Доли и дроби
6 ступень. Математика. Доли и дроби Умножение чисел, запись которых заканчивается нулями
Умножение чисел, запись которых заканчивается нулями Объём фигуры. Единицы объёма
Объём фигуры. Единицы объёма Применение распределительного свойства умножения
Применение распределительного свойства умножения Краткосрочная образовательная практика Весёленькие ребусы
Краткосрочная образовательная практика Весёленькие ребусы Криволинейные интегралы
Криволинейные интегралы Устный счет
Устный счет Математика уступает свои крепости лишь сильным и смелым
Математика уступает свои крепости лишь сильным и смелым Треугольник. Геометрическая фигура
Треугольник. Геометрическая фигура Начальные геометрические сведения
Начальные геометрические сведения Свойства откладывания отрезков и углов
Свойства откладывания отрезков и углов Векторные пространства
Векторные пространства Случайные события и вероятность
Случайные события и вероятность Задачи на построения с помощью циркуля и линейки
Задачи на построения с помощью циркуля и линейки Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс 20231119_urok_geometrii_v_7_klasse_svoystva_parallelnosti_pryamyh
20231119_urok_geometrii_v_7_klasse_svoystva_parallelnosti_pryamyh Процесс решения задачи. 6 класс
Процесс решения задачи. 6 класс Презентация к уроку математике в 4 классе по теме Умножение многозначного числа на однозначное число.
Презентация к уроку математике в 4 классе по теме Умножение многозначного числа на однозначное число.