Содержание
- 2. I. Определение векторного пространства I.1. Определение и примеры I.2. Пространства и оболочки
- 3. Определение 1.1: Векторное пространство( V, +, ,; F) Векторное пространство (над R) состоит из множества V
- 4. Пример 1.2: R2 R2 является векторным пространством, если и Пример 1.3: Плоскость в пространстве R3. есть
- 5. Пример 1.4: Пусть Тогда V есть векторное пространство над F. Определение 1.5: Пространство с одним элементом
- 6. Пример 1.5: Пространство многочленов степени не выше n Сложение: Умножение на число: Нулевой элемент: Обозначим Например,
- 7. Пример 1.6: Пространство функций Множество { f | f : R → R} действительных функций от
- 8. Замечания: Определения могут быть другими. Данное определение наиболее часто встречается в математических работах. Лемма 1.7: Для
- 9. Определение 1.8: Линейная комбинация Пусть S - подмножество векторного пространства V, и - числа, тогда есть
- 10. I.2. Подпространства и оболочки Определение 2.1: Подпространство Для любого векторного пространства, подпространство есть подмножество, которое само
- 11. Пример 2.3: { 0 } есть тривиальное подпространство Rn. Rn есть подпространство Rn.
- 12. Лемма 2.4: Пусть S есть непустое подмножество векторного пространства V над полем F. Тогда следующие утверждения
- 13. Определение 2.5: Линейная оболочка Пусть S = { s1 , …, sn | sk ∈ V
- 14. Пример 2.7: Доказательство: Действительно, для произвольного вектора из соотношения получаем эта система имеет единственное решение Так
- 15. Определение 2.8. Полнота Подмножество S векторного пространства V называется полным если span S = V.
- 17. Скачать презентацию














 Differentiation. A “derivative”,
Differentiation. A “derivative”, Полигон, гистограмма и кумулятивная кривая
Полигон, гистограмма и кумулятивная кривая Свойства действий с рациональными числами
Свойства действий с рациональными числами Презентация Задачи в стихах
Презентация Задачи в стихах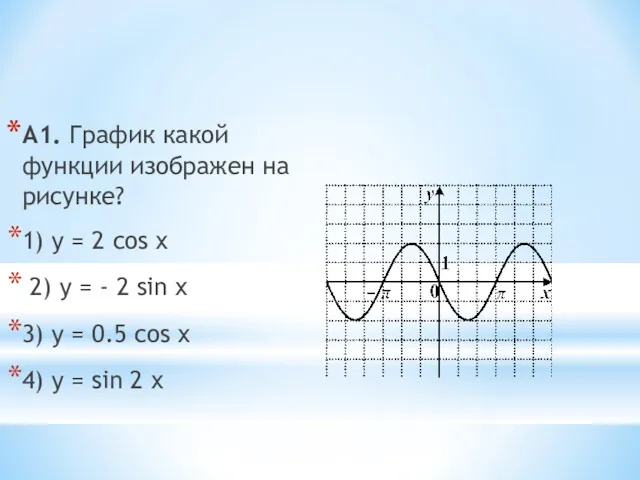 График функции. Устный счет
График функции. Устный счет Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Уравнение касательной к графику функции
Уравнение касательной к графику функции Использование числовых неравенств при решении нестандартных заданий ЕГЭ
Использование числовых неравенств при решении нестандартных заданий ЕГЭ Презентация к уроку Числа от 1 до 100
Презентация к уроку Числа от 1 до 100 Решение квадратных уравнений различными способами
Решение квадратных уравнений различными способами Уравнения. (2 класс)
Уравнения. (2 класс) Презентация Уроки с Мальвиной
Презентация Уроки с Мальвиной Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики
Возможности формирования универсальных учебных действий (УУД) при изучении начального курса математики Trigonometriýa
Trigonometriýa Сложение и вычитание дробей с одинаковым знаменателем
Сложение и вычитание дробей с одинаковым знаменателем Умножение и деление рациональных чисел
Умножение и деление рациональных чисел Луч и угол
Луч и угол Игра Экология и математика
Игра Экология и математика Числовые домики
Числовые домики Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов
Первообразная. Неопределенный интеграл и его свойства. Таблица основных интегралов Непосредственная образовательная деятельность по теме Путешествие с Красной шапочкой для детей среднего дошкольного возраста
Непосредственная образовательная деятельность по теме Путешествие с Красной шапочкой для детей среднего дошкольного возраста Наш мир – это удивительный мир симметрии
Наш мир – это удивительный мир симметрии Объемы тел. Площадь
Объемы тел. Площадь Матрицы. Действия с матрицами
Матрицы. Действия с матрицами Готовимся к ГИА. Элементарные функции
Готовимся к ГИА. Элементарные функции Открытый урок математики в 1-м классе (УМК Гармония). Предметный смысл сложения. Знакомство с терминологией.
Открытый урок математики в 1-м классе (УМК Гармония). Предметный смысл сложения. Знакомство с терминологией. Урок математики. 1 класс (2 часть). Тема: Части фигур УМК Школа 2100
Урок математики. 1 класс (2 часть). Тема: Части фигур УМК Школа 2100 Задачи на построение треугольника
Задачи на построение треугольника