Содержание
- 2. Если ты услышишь, что кто-то не любит математику, не верь. Её нельзя не любить - её
- 3. Цель реферата: Научиться правильно отображать формулы с применением различных способов решения уравнений Задачи реферата: - улучшить
- 4. История квадратных уравнений Необходимость решать уравнения еще в древности была вызвана потребностью решать задачи, связанные с
- 6. Решение уравнений способом «переброски» Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета
- 7. Свойства коэффициентов квадратного уравнения А. ах2 + bх + с = 0, а ≠ 0 1.Если
- 8. Свойства коэффициентов квадратного уравнения А. ах2 + bх + с = 0, а ≠ 0 2.
- 9. Свойства коэффициентов квадратного уравнения Б. ах2 + bх + с = 0, а ≠ 0 Если
- 10. Свойства коэффициентов квадратного уравнения В. уравнение x2 + px + q = 0 совпадает с уравнением
- 11. По теореме о секущих имеем ОВ∙ОD = ОА ∙ ОС, откуда ОС = Центр окружности находиться
- 12. 1. Радиус окружности больше ординаты центра (AS > SK, или R > ), окружность пересекает ось
- 13. Радиус окружности равен ординате центра (AS = SВ, или R = ), окружность касается оси Ох
- 14. Радиус окружности меньше ординаты центра (AS R AS Нет решения S A B Решение квадратных уравнений
- 15. 1. Радиус окружности больше ординаты центра (AS > SK, или R > ), окружность пересекает ось
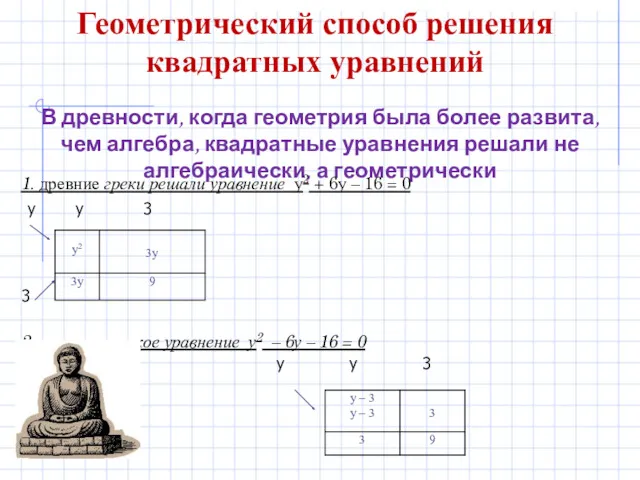
- 16. Геометрический способ решения квадратных уравнений В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения
- 17. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств
- 18. методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников
- 20. Скачать презентацию















 Презентация к уроку. Математика в 4 классе
Презентация к уроку. Математика в 4 классе Нумерация чисел в пределах 1000
Нумерация чисел в пределах 1000 Статистикалық болжамдарды тексеру
Статистикалық болжамдарды тексеру Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Методы непараметрического спектрального анализа. Метод периодограмм
Методы непараметрического спектрального анализа. Метод периодограмм Задачи на деление.
Задачи на деление. Основные правила комбинаторики
Основные правила комбинаторики Первообразная функции и неопределенный интеграл
Первообразная функции и неопределенный интеграл Вспоминаем пройденное урок 55
Вспоминаем пройденное урок 55 Удивительный мир симметрии
Удивительный мир симметрии Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Параллельность прямых и плоскостей
Параллельность прямых и плоскостей Сложение и вычитание десятичных дробей. 5 класс
Сложение и вычитание десятичных дробей. 5 класс 20231122_mnogochleny
20231122_mnogochleny Векторы в пространстве
Векторы в пространстве Координаты на прямой. 6 класс
Координаты на прямой. 6 класс Скорость сближения и удаления
Скорость сближения и удаления Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов Самостоятельная работа на обратные дроби
Самостоятельная работа на обратные дроби Геометрия. Основная теория для подготовки к ОГЭ
Геометрия. Основная теория для подготовки к ОГЭ Определение значений коэффициентов квадратичной функции по графику
Определение значений коэффициентов квадратичной функции по графику Урок математики по теме Решение задач
Урок математики по теме Решение задач Конспект урока математики во 2 классе Таблица умножения и деления на 6
Конспект урока математики во 2 классе Таблица умножения и деления на 6 Интегральное исчисление. Неопределенный интеграл
Интегральное исчисление. Неопределенный интеграл Практико-ориентированные задачи
Практико-ориентированные задачи Функция y=k/x, её свойства и график
Функция y=k/x, её свойства и график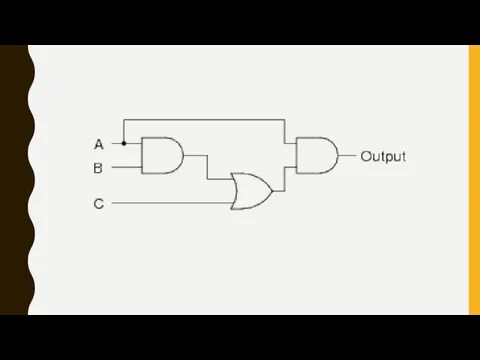 Simplify logical expressions
Simplify logical expressions Проект Наше село в числах и величинах
Проект Наше село в числах и величинах