Слайд 2

Вопросы темы
Понятие первообразной.
Неопределенный интеграл и его свойства.
Таблица основных интегралов.
Слайд 3

Слайд 4

Определение
Функция F(x) называется первообразной функцией для функции f(x) на промежутке X,
если в каждой точке этого промежутка
Слайд 5
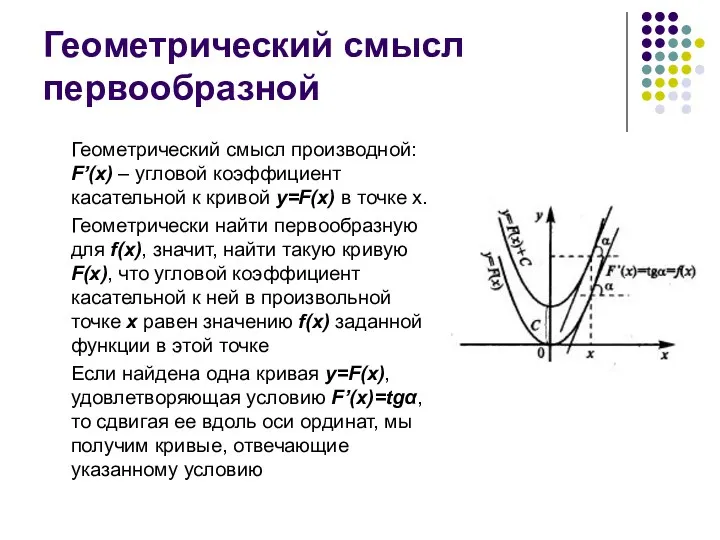
Геометрический смысл первообразной
Геометрический смысл производной: F’(x) – угловой коэффициент касательной к
кривой y=F(x) в точке x.
Геометрически найти первообразную для f(x), значит, найти такую кривую F(x), что угловой коэффициент касательной к ней в произвольной точке x равен значению f(x) заданной функции в этой точке
Если найдена одна кривая y=F(x), удовлетворяющая условию F’(x)=tgα, то сдвигая ее вдоль оси ординат, мы получим кривые, отвечающие указанному условию
Слайд 6

Теорема
Если F1(x) и F2(x) – первообразные для функции f(x) на промежутке
X, то найдется такое число C, что будет справедливо равенство
Слайд 7

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
И ЕГО СВОЙСТВА
Слайд 8

Определение
Совокупность всех первообразных для функции f(x) на промежутке X, называется неопределенным
интегралом от функции f(x)
f(x) – подынтегральная функция
f(x)dx – подынтегральное выражение
F(x) – некоторая первообразная для f(x)
C – произвольная константа
Слайд 9

Свойства
неопределенного интеграла
Производная от неопределенного интеграла равна подынтегральной функции:
Слайд 10

Свойства
неопределенного интеграла
Дифференциал неопределенного интеграла равен подынтегральному выражению:
Слайд 11

Свойства
неопределенного интеграла
Неопределенный интеграл от дифференциала некоторой функции равен этой функции
с точностью до постоянного слагаемого:
Слайд 12

Свойства
неопределенного интеграла
Постоянный множитель можно выносить за знак интеграла:
Слайд 13

Свойства
неопределенного интеграла
Интеграл от алгебраической суммы двух функций равен такой же
сумме интегралов от этих функций:
Слайд 14

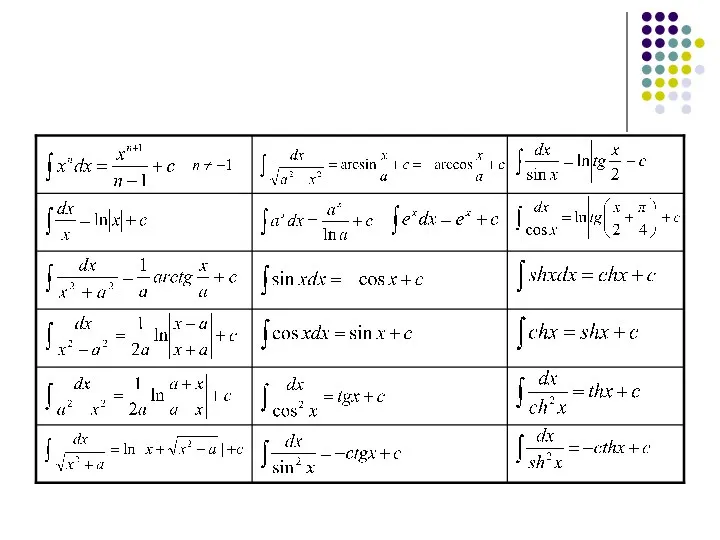
ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
Слайд 15
Слайд 16

НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ
ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
Слайд 17
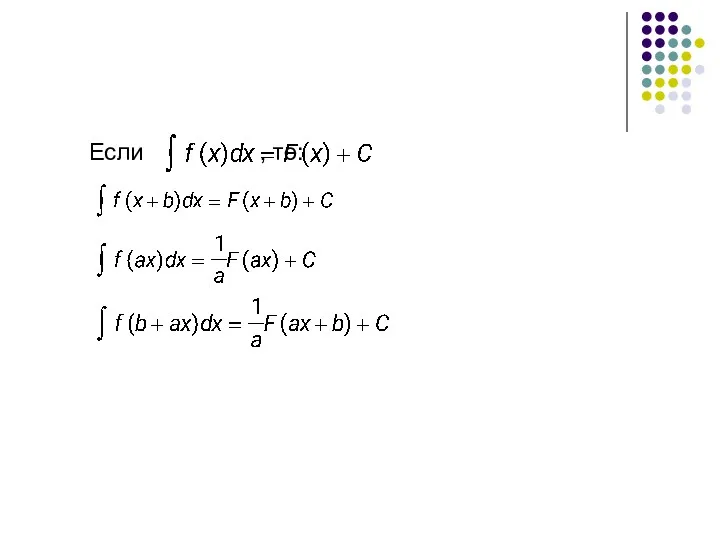
Слайд 18

СПЕЦИАЛЬНЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
Слайд 19

Интегрирование методом замены переменной (метод подстановки)
Пусть ,
тогда:
где t(x) - дифференцируемая
монотонная функция
Слайд 20

Методы замены переменной
Если в подынтегральной функции удаётся сразу заметить оба сомножителя,
и f(t(x)), и t’(x), то замена переменной осуществляется подведением множителя t’(x) под знак дифференциала: t’(x)dx = dt, и задача сводится к вычислению интеграла
Слайд 21

Методы замены переменной
Замену переменной можно осуществлять формальным сведением подынтегрального выражения к
новой переменной
Слайд 22

Интегрирование по частям
Пусть u(x) и v(x) - функции, имеющие непрерывные частные
производные.
Тогда по формуле дифференцирования произведения
d(uv) = u∙dv + v∙du → u∙dv = d(uv) - v∙du.
Находим неопределённые интегралы для обеих частей этого равенства (при этом ):
Или:
Слайд 23

Сведение интеграла
«к самому себе»
С помощью интегрирования по частям (возможно, неоднократного)
интеграл выражается через такой же интеграл; в результате получается уравнение относительно этого интеграла, решая которое, находим значение интеграла
Слайд 24

Рекуррентные соотношения
Если подынтегральная функция зависит от некоторого параметра n, и получено
соотношение, которое выражает интеграл через аналогичный интеграл с меньшим значением n, то это соотношение и называется рекуррентным соотношением















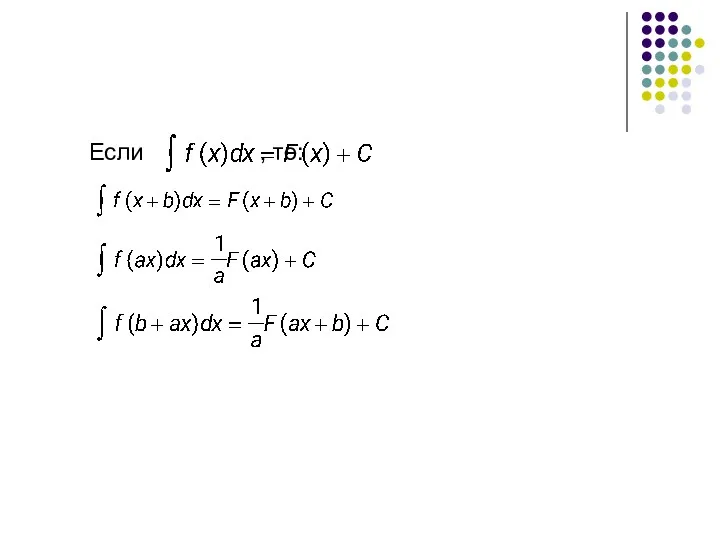







 Описательная статистика
Описательная статистика Интегрированный урок: математика + биология. Простые и сложные листья
Интегрированный урок: математика + биология. Простые и сложные листья Математика и музыка. Реалити-шоу
Математика и музыка. Реалити-шоу Цена. Количество. Стоимость
Цена. Количество. Стоимость Длина окружности (6 класс)
Длина окружности (6 класс) Презентация к уроку математики по теме Задачи на движение
Презентация к уроку математики по теме Задачи на движение Непрерывная случайная величина. Равномерное, показательное и нормальное распределение
Непрерывная случайная величина. Равномерное, показательное и нормальное распределение решение неравенств второй степени с помощью графика квадратичной функции
решение неравенств второй степени с помощью графика квадратичной функции Презентация к уроку русского языка в 4 классе Неопределённая форма глагола
Презентация к уроку русского языка в 4 классе Неопределённая форма глагола Математические предложения
Математические предложения Вычитание вида 12 -
Вычитание вида 12 - Транспортные сети. Поиск максимального потока в сети. (Лекция 10)
Транспортные сети. Поиск максимального потока в сети. (Лекция 10) компьютерная математическая игра Космическое путешествие (1-2 классы)
компьютерная математическая игра Космическое путешествие (1-2 классы) Определение модуля числа
Определение модуля числа Дециметр. Урок математики 1 класс
Дециметр. Урок математики 1 класс Эконометрика. Гетероскедастичность случайной составляющей
Эконометрика. Гетероскедастичность случайной составляющей Графический диктант. Верно или не верно
Графический диктант. Верно или не верно Крестики-нолики
Крестики-нолики Функция у=х 3. График функции
Функция у=х 3. График функции Комбинация призмы и цилиндра
Комбинация призмы и цилиндра Приемы письменного умножения в пределах 1000
Приемы письменного умножения в пределах 1000 Загадка числа Пи
Загадка числа Пи Жазық фигураның жазықтыққа ортогональ проекциясы және оның ауданы
Жазық фигураның жазықтыққа ортогональ проекциясы және оның ауданы Умножение и деление десятичных дробей. Контрольная работа
Умножение и деление десятичных дробей. Контрольная работа урок математики в 3 классе по теме Закрепление таблицы умножения и деления на 2 и 3
урок математики в 3 классе по теме Закрепление таблицы умножения и деления на 2 и 3 Решение неравенств с одной переменной. 8 класс
Решение неравенств с одной переменной. 8 класс Отклонение. Дисперсия
Отклонение. Дисперсия Площадь прямоугольника
Площадь прямоугольника