Содержание
- 2. Студент должен знать понятия неопределённого и определённого интегралов; свойства интегралов; таблицу неопределённых интегралов; методы интегрирования; формулу
- 3. Заполните таблицу
- 4. Первообразная (определение) y = F(x), y = f(x), D(F) = D(f) = X, F(x) – первообразная
- 5. Определить первообразную функции f(x) = 3x2 F(x) = x3 т.к. F′(x) = (x3)′ = 3x2 =
- 6. Определить первообразную функции f(x) = 3x2 1. F(x) = x3+1, т.к. F′(x) = (x3+1)′ = 3x2+0
- 7. Теорема 1 Функция f(x), имеет бесконечное множество первообразных вида F(x)+С.
- 8. Неопределённый интеграл f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.
- 9. Свойства неопределённого интеграла
- 10. Теорема 2 Дифференциал интеграла функции равен подынтегральному выражению.
- 11. Теорема 3 Производная интеграла равна подынтегральной функции.
- 12. Теорема 4 Интеграл производной функции равен сумме этой функции с произвольной константой.
- 13. Теорема 5 Интеграл суммы равен сумме интегралов
- 14. Теорема 6 Постоянный множитель выносится за знак интеграла
- 15. Основные формулы интегрирования
- 16. Интеграл дифференциала аргумента
- 17. Интеграл степенной функции
- 18. Интеграл обратной пропорциональности
- 19. Интеграл экспоненциальной функции
- 20. Интеграл показательной функции
- 21. Интеграл функции косинуса
- 22. Интеграл функции синуса
- 23. Методы интегрирования Непосредственное интегрирование Метод подстановки (замены переменной) Метод интегрирования по частям
- 24. Непосредственное интегрирование Найти:
- 26. Метод подстановки (замены переменной) Найти:
- 27. Введение подстановки
- 29. Метод интегрирования по частям
- 30. Найти: Чтобы воспользоваться формулой необходимо выбрать функцию u и дифференциал dυ Пусть u = x и
- 31. Выберем функцию u и дифференциал dυ иначе: Пусть u = lnx и dυ = xdx. и
- 32. Образец оформления
- 34. Определённый интеграл Определённый интеграл функции y=f(x) есть число, значение которого зависит от вида этой функции и
- 35. Определённый интеграл f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, a – нижний предел интегрирования b
- 36. Формула Ньютона-Лейбница
- 37. Свойства определённого интеграла
- 38. Теорема 7 (аддитивность)
- 39. Теорема 8
- 40. Теорема 9
- 41. Теорема 10
- 42. Вычисление определённых интегралов Вычислить:
- 43. Вычисление определённых интегралов
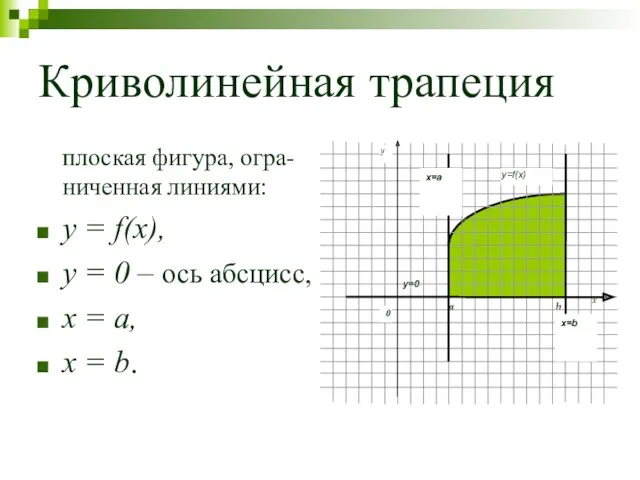
- 44. Криволинейная трапеция плоская фигура, огра-ниченная линиями: y = f(x), y = 0 – ось абсцисс, x
- 45. Площадь криволинейной трапеции
- 46. Вычисление площадей плоских фигур Вычислить площадь фигуры, ограниченной линиями:
- 47. (кв.ед.).
- 48. Дифференциальные уравнения
- 49. Дифференциальное уравнение* – это уравнение, связывающее независимую переменную x, её функцию y, производные различных порядков этой
- 50. Решить ДУ – это значит, найти множество всех функций, которые удовлетворяют данному ДУ: Такое множество функций
- 51. Обыкновенное ДУ* – это ДУ, которое имеет только одну независимую переменную (например, х или t). ДУ
- 52. Порядок* ОДУ – это порядок старшей производной: y’ + 1 = 0 – ОДУ первого порядка;
- 53. Решение ОДУ ОДУ: y’ = x2; Одно из решений: y = (1/3)⋅x3; Проверка: ((1/3)⋅x3)’ = (1/3)⋅(x3)’
- 54. Общее решение ОДУ – это множество решений, содержащее ВСЕ без исключения решения этого дифференциального уравнения.
- 55. Частное решение ОДУ – одно из множества решений ОДУ, удовлетворяющее изначально заданным дополнительным условиям: ОДУ: y’
- 56. Задача Коши – это задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям.
- 57. ОДУ с разделяющимися переменными – это уравнение, которое возможно преобразовать таким образом, что правая часть будет
- 58. Пример 1 Найти общее решение ОДУ xy’ = y. Решение ОДУ происходит в несколько этапов:
- 59. Этап 1: расшифровка производной Запишем: y’ = dy/dx Тогда: xy’ = y ⇒ x⋅dy/dx = y;
- 60. Этап 2: разделение переменных x⋅dy/dx = y; По свойству пропорции, перенесём «крест-накрест» х и dx вправо,
- 61. Этап 3: интегрирование Найдём интегралы левой и правой частей уравнения: ∫(dy/y) = ∫(dх/x); ln|y| = ln|x|
- 62. Этап 4: нахождение y в явном виде Найдём общее решение (функцию y) в явном виде: ln|y|
- 63. Пример 2 (задача Коши) Найти частное решение дифференциального уравнения y’ = –2y, удовлетворяющее начальному условию y(0)
- 64. Этап 1: расшифровка производной Запишем: y’ = dy/dx Тогда: y’ = –2y ⇒ dy/dx = –2y;
- 65. Этап 2: разделение переменных dy/dx = –2y; По свойству пропорции, перенесём «крест-накрест» dx вправо, а y
- 66. Этап 3: интегрирование Найдём интегралы левой и правой частей уравнения: dy/y = dх; ∫(dy/y) = ∫(–2dх);
- 67. Этап 4: нахождение y в явном виде Найдём общее решение (функцию y) в явном виде: ln|y|
- 68. Этап 5: нахождение частного решения Найдём частное решение для y(0) = 2: При х = 0:
- 69. Итоги свойства интегралов; таблица неопределённых интегралов; методы интегрирования; формула Ньютона-Лейбница; дифференциальные уравнения; задача Коши.
- 70. Домашнее задание К практическому занятию №3: Теория – лекционный материал; Письменно – упражнения для самостоятельной работы.
- 72. Скачать презентацию


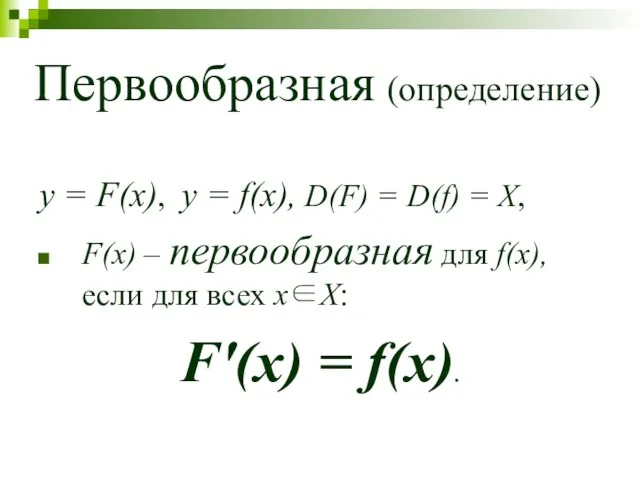



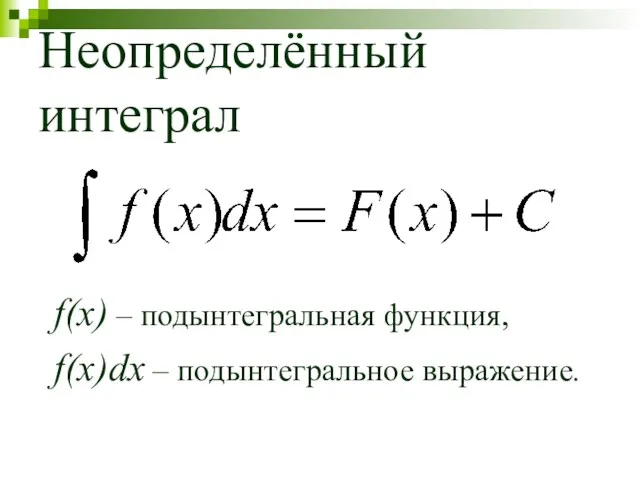







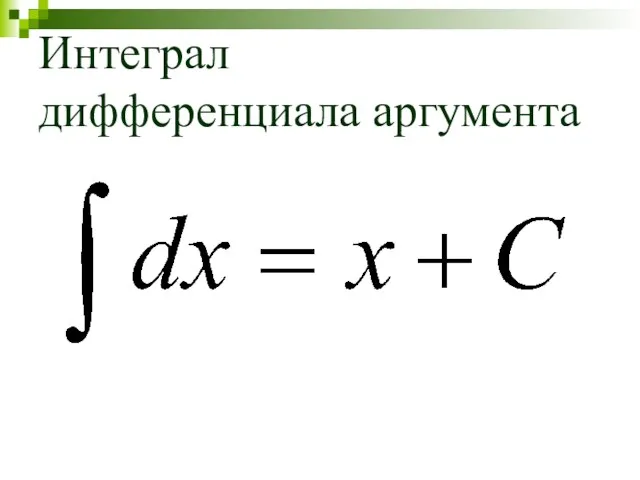
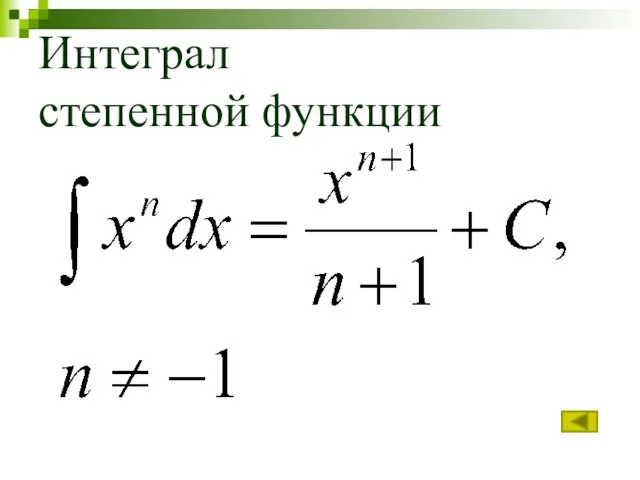
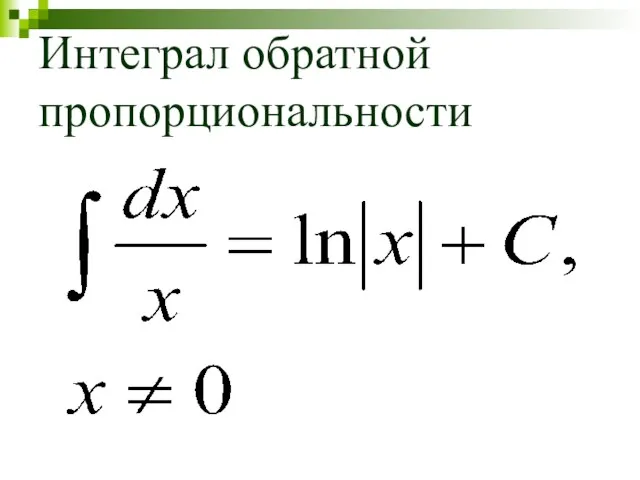
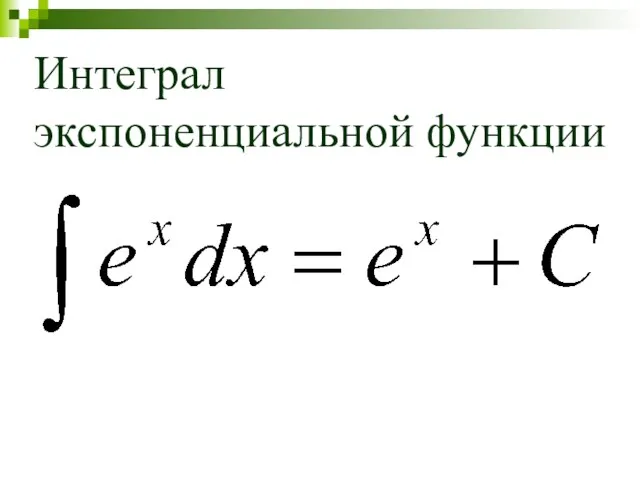
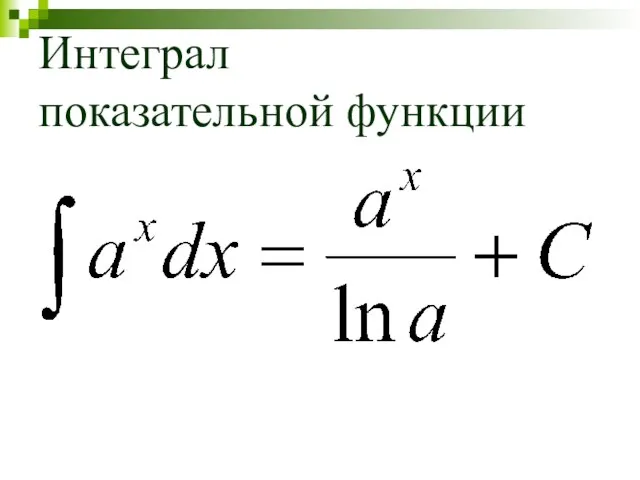




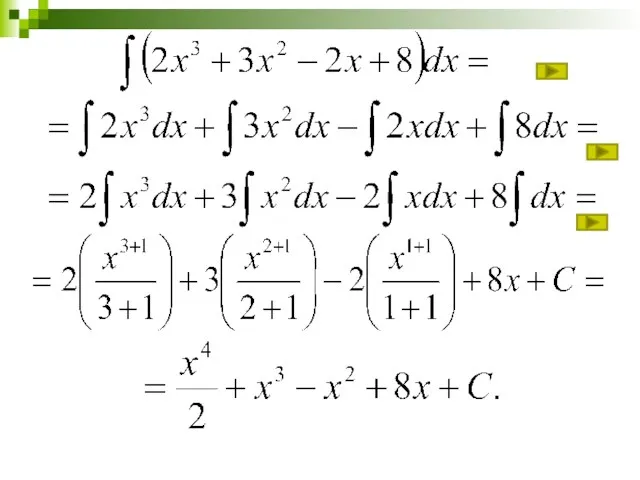


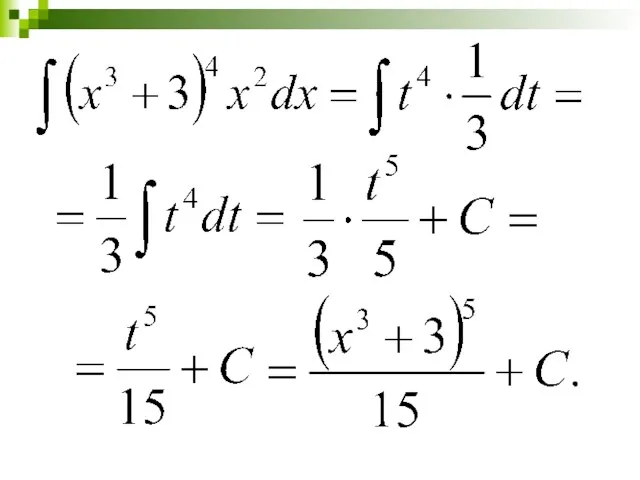
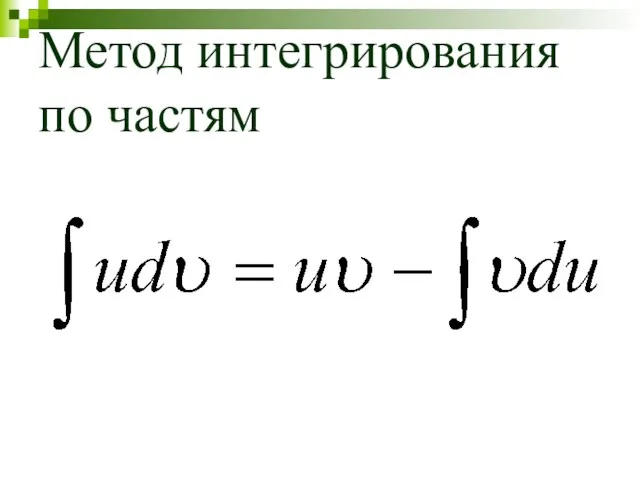



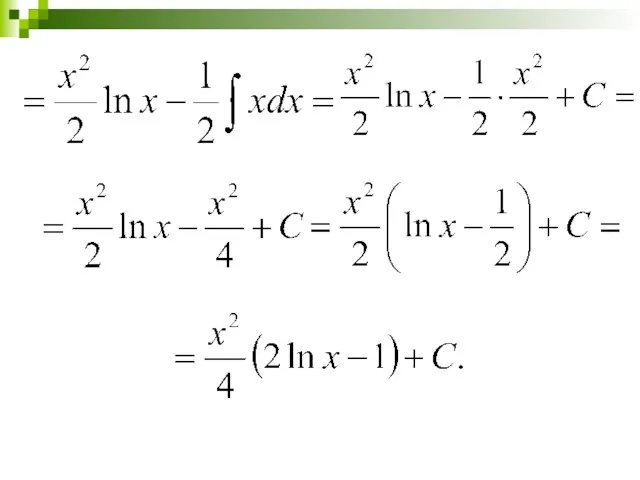










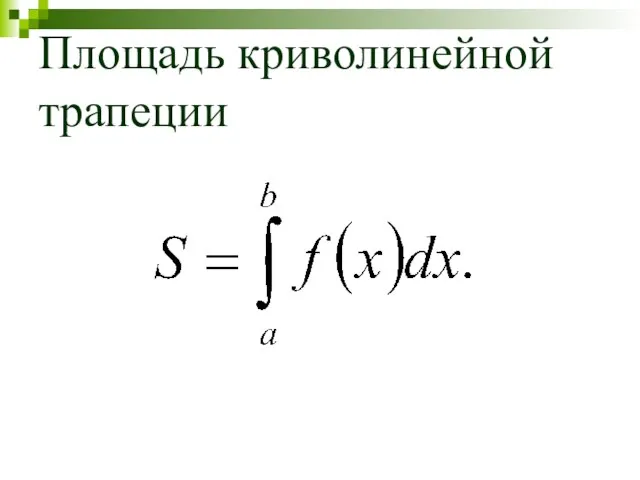

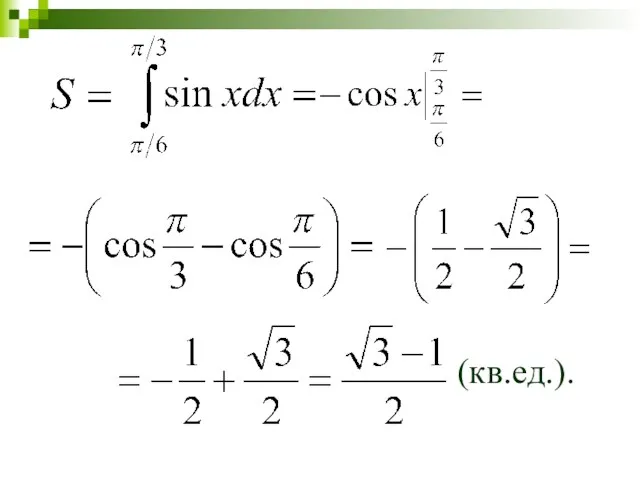























 Идеальный математик XVIII века - Леонард Эйлер. Типы кругов Эйлера
Идеальный математик XVIII века - Леонард Эйлер. Типы кругов Эйлера Повторение. Алгебра 9 класс
Повторение. Алгебра 9 класс Метр — одиниця довжини. Урок №44
Метр — одиниця довжини. Урок №44 Интегрированный урок во 2 классе по английскому языку и математике
Интегрированный урок во 2 классе по английскому языку и математике Математическая логика. (Тема 2)
Математическая логика. (Тема 2) Симметрия вокруг нас
Симметрия вокруг нас Диалоговое взаимодействие учащихся и учителя на уроке математики
Диалоговое взаимодействие учащихся и учителя на уроке математики Формулы корней квадратных уравнений
Формулы корней квадратных уравнений Деление с остатком
Деление с остатком Решение задач на проценты. Основные задачи на проценты
Решение задач на проценты. Основные задачи на проценты Random variables – discrete random variables. Week 6 (2)
Random variables – discrete random variables. Week 6 (2) Степень с рациональным показателем
Степень с рациональным показателем Применение производной к исследованию функции
Применение производной к исследованию функции Методика обучения математике в начальных классах школы как наука
Методика обучения математике в начальных классах школы как наука Урок+презентация по математике Путешествие в страну Математики для 5 класса
Урок+презентация по математике Путешествие в страну Математики для 5 класса Решение задач. Признаки равенства треугольников
Решение задач. Признаки равенства треугольников Многогранник та його елементи. Правильні многогранники. Призма, види призм. Площа та об’єм призми
Многогранник та його елементи. Правильні многогранники. Призма, види призм. Площа та об’єм призми Периметр прямоугольника
Периметр прямоугольника Математический пакет MahCad
Математический пакет MahCad Решение неравенств методом интервалов
Решение неравенств методом интервалов Приемы деления числа
Приемы деления числа Исторические комбинаторные задачи. Различные комбинации трех элементов
Исторические комбинаторные задачи. Различные комбинации трех элементов Викторина Путешествие по стране Математика
Викторина Путешествие по стране Математика Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Решение систем линейных алгебраических уравнений (СЛАУ)
Решение систем линейных алгебраических уравнений (СЛАУ) График и свойства степенной функции. 10 класс
График и свойства степенной функции. 10 класс Дидактическая игра Колесо фортуны
Дидактическая игра Колесо фортуны УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ
УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ