Содержание
- 2. Основные понятия Комплексным числом z называется выражение вида z=a+ib, где a и b – действительные числа,
- 3. Действия над комплексными числами 1) Действия над комплексными числами, заданными в алгебраической форме а) Сложение комплексных
- 4. в) Умножение комплексных чисел Произведением комплексных чисел z1=x1+y1i и z2=x2+y2i называется комплексное число, определяемое равенством z=z1
- 5. г) Деление комплексных чисел Деление определяется как действие, обратное умножению. Частным двух комплексных чисел z1 и
- 6. На практике вместо полученной формулы используют следующий прием: умножают числитель и знаменатель дроби на число, сопряженное
- 7. д) Возведение комплексного числа, заданного в алгебраической форме в n-ю степень Выпишем целые степени мнимой единицы:
- 8. При возведении комплексного числа a+bi во вторую и третью степень пользуются формулой для квадрата и куба
- 9. е) Извлечение квадратного корня из комплексного числа Квадратным корнем из комплексного числа называется такое комплексное число,
- 10. Пример 4. Извлечем квадратный корень из комплексного числа z=5+12i. Решение. Обозначим квадратный корень из числа z
- 11. Геометрическое изображение комплексных чисел Всякое комплексное число z=x+iy можно изобразить точкой M(x;y) плоскости xOy такой, что
- 12. Часто вместо точек на плоскости берут их радиус-векторы т.е. векторы, началом которых служит точка O(0;0), концом
- 13. Формы записи комплексных чисел Запись числа в виде z=x+iy называют алгебраической формой комплексного числа. Из рисунка
- 14. При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного
- 15. Решение. Комплексное число z=x+iy в тригонометрической форме имеет вид z=r(cosφ +isinφ), где 1) z1=1+i (число z1
- 16. Рассмотрим показательную функцию w=ez, где z=x+iy - комплексное число. Можно показать, что функция w может быть
- 17. Из этих двух уравнений получаем: Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции
- 18. Действия над комплексными числами, заданными в тригонометрической форме Рассмотрим два комплексных числа z1 и z2 ,
- 19. б) Частное двух комплексных чисел Пусть заданы комплексные числа z1 и z2 ≠ 0. Рассмотрим частное
- 20. Пример 5. Даны два комплексных числа Найдите Решение. 1) Используя формулу . получаем Следовательно, 2) Используя
- 21. в) Возведение комплексного числа, заданного в тригонометрической форме в n-ю степень Из операции умножения комплексных чисел
- 22. Пример 6. Найти формулы sin2ϕ и cos2ϕ. Решение. Рассмотрим некоторое комплексное число Тогда с одной стороны
- 23. г) Извлечение корня п-ой степени из комплексного числа Корнем п-ой степени из комплексного числа z называется
- 24. Таким образом, извлечение корня n-ой степени из комплексного числа z всегда возможно и дает n различных
- 25. Запишем все значения : при при при Ответ:
- 26. Где используются комплексные числа в реальной жизни? Электротехника и электроника: Расчеты в переменных тока, анализ электрических
- 27. Вопросы для самоконтроля 1. Сформулируйте определение комплексного числа. 2. Какое комплексное число называется чисто мнимым? 3.
- 29. Скачать презентацию


























 Умножение вектора на число
Умножение вектора на число Деление вида 63 : 3
Деление вида 63 : 3 Игровые технологии на уроках математики в 5-6 классах
Игровые технологии на уроках математики в 5-6 классах Деление на группы по несколько предметов.
Деление на группы по несколько предметов. Параллельные прямые. Задачи на готовых чертежах
Параллельные прямые. Задачи на готовых чертежах Формулы площадей геометрических фигур
Формулы площадей геометрических фигур Определение и знаки синуса, косинуса и тангенса угла
Определение и знаки синуса, косинуса и тангенса угла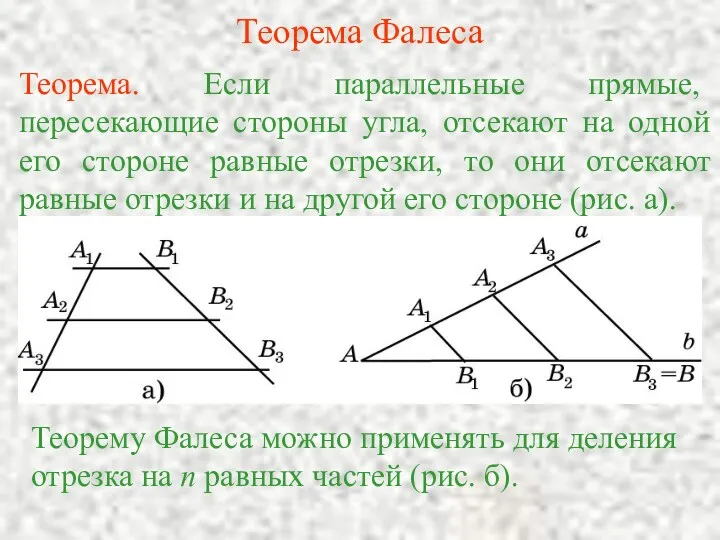 Теорема Фалеса
Теорема Фалеса Математическая игра Проще простого
Математическая игра Проще простого Натуральные числа. 7 класс
Натуральные числа. 7 класс Вычитание вида 11-
Вычитание вида 11- Свойства и признаки параллельных прямых
Свойства и признаки параллельных прямых Луч и угол
Луч и угол Презентация Математика вокруг нас
Презентация Математика вокруг нас Презентация к уроку математики во 2 классе по теме: Час.Минута. Определение времени по часам
Презентация к уроку математики во 2 классе по теме: Час.Минута. Определение времени по часам Кривые второго порядка
Кривые второго порядка Организация лабораторных работ по наглядной геометрии для учащихся 5-6 классов
Организация лабораторных работ по наглядной геометрии для учащихся 5-6 классов Методы решения уравнений
Методы решения уравнений Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями Функции у=sin x и y = cos x и их графики
Функции у=sin x и y = cos x и их графики Занятие по математике Простоквашино
Занятие по математике Простоквашино Параллельные плоскости
Параллельные плоскости Арифметическая прогрессия
Арифметическая прогрессия Десятичные дроби и метрическая система мер
Десятичные дроби и метрическая система мер Тренажер по математике №1. Сложение и вычитание
Тренажер по математике №1. Сложение и вычитание Обходы графов
Обходы графов Случайные величины. Дискретная случайная величина
Случайные величины. Дискретная случайная величина Из опыта работы по подготовке учащихся 9-х классов к ОГЭ по математике
Из опыта работы по подготовке учащихся 9-х классов к ОГЭ по математике