Содержание
- 2. — действительная часть — мнимая часть — число, комплексно сопряженное к
- 3. Действия над комплексными числами Сложение Умножение Деление
- 4. п.2. Геометрическая интерпретация. x y O
- 5. Формы записи комплексных чисел Алгебраическая Тригонометрическая x y O
- 6. x y O Число r называется модулем числа и обозначается
- 7. Угол между положительным направлением действительной оси и вектором z называется аргументом и обозначается Значение аргумента, заключенное
- 8. Замечание 1. Показательная Формула Эйлера:
- 9. п.3. Свойства модуля и аргумента. 1) Доказательство.
- 10. Замечание 2. Замечание 3. Пусть Тогда — формула Муавра
- 11. Замечание 4. Пусть
- 12. 2) Доказательство. Свойство 1)
- 13. 3) 4) Модуль разности равен расстоянию между и . x y O
- 14. п.4. Последовательности комплексных чисел. Число z называется пределом последовательности , если
- 15. Теорема 1. Замечание 5. x y O z
- 16. Доказательство. Необходимость. Пусть Замечание 5
- 17. Достаточность. Пусть Замечание 5
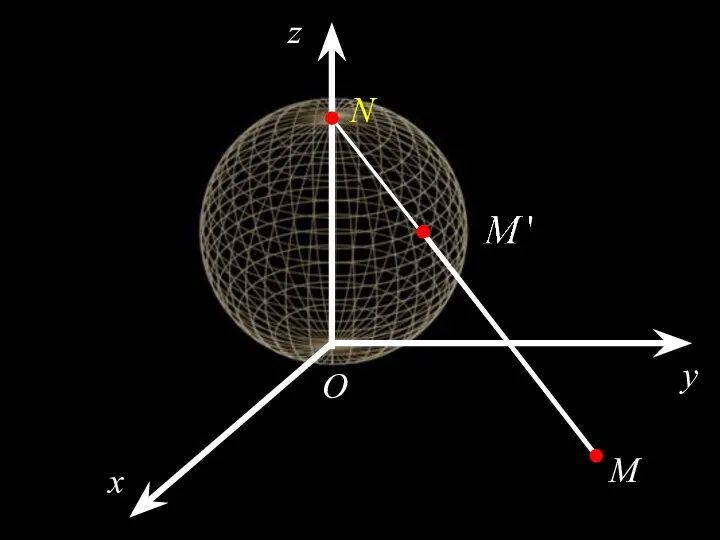
- 18. п.5. Бесконечность и стереографическая проекция. Последовательность называется сходящейся к , если
- 19. -окрестностью точки называется внешность круга с центром в начале координат и радиусом : -окрестностью конечной точки
- 20. Точка z называется пределом последовательности , если для все точки последовательности, начиная с некоторого номера, принадлежат
- 21. x y z N M O
- 23. Скачать презентацию















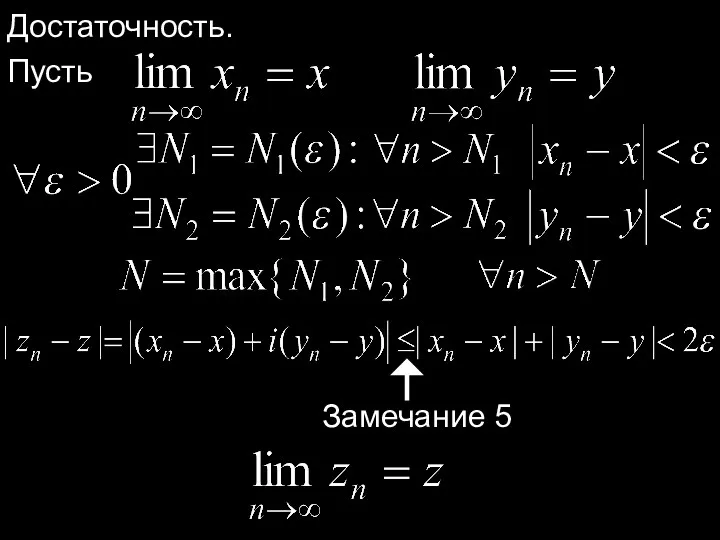



 Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями Көп айнымалылар функциясы
Көп айнымалылар функциясы Теорема Менелая. Решение задач
Теорема Менелая. Решение задач Уравнения. Путешествие по Солнечной системе
Уравнения. Путешествие по Солнечной системе Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Многоугольник. Прямоугольник. Площадь многоугольника
Многоугольник. Прямоугольник. Площадь многоугольника Парная линейная регрессионная модель
Парная линейная регрессионная модель Сумма углов треугольника
Сумма углов треугольника Задачи с экономическим содержанием
Задачи с экономическим содержанием Нахождение неизвестных компонентов сложения и вычитания
Нахождение неизвестных компонентов сложения и вычитания Перпендикулярные прямые
Перпендикулярные прямые Презентация для викторины по геометрии 4 класс
Презентация для викторины по геометрии 4 класс Фрагмент урока по математике в 1 классе.
Фрагмент урока по математике в 1 классе. 20190116_prezentatsiya_1
20190116_prezentatsiya_1 презентацияРазноцветная математика
презентацияРазноцветная математика Пропорции – равенство двух отношений
Пропорции – равенство двух отношений Многоугольники. Урок геометрии в 8 классе
Многоугольники. Урок геометрии в 8 классе детская презентация Единицы длины
детская презентация Единицы длины Фрагмент к уроку математики Трапеция
Фрагмент к уроку математики Трапеция Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Развитие логического мышления на уроках математики
Развитие логического мышления на уроках математики Задачи и содержание учебной дисциплины Метрология, стандартизация и сертификация
Задачи и содержание учебной дисциплины Метрология, стандартизация и сертификация Круговые диаграммы
Круговые диаграммы Метод координат и метод векторов при решении задач
Метод координат и метод векторов при решении задач Статистическая обработка данных
Статистическая обработка данных Функции переменных. Математический анализ. Лекции № 11-12
Функции переменных. Математический анализ. Лекции № 11-12 Числовые и буквенные выражения
Числовые и буквенные выражения Округление натуральных чисел
Округление натуральных чисел