Содержание
- 2. Повторите материал по теме: «Цилиндр. Площадь его поверхности». Ответьте на вопросы самопроверки.
- 3. Вопрос №1: Какая фигура является основанием цилиндра? а) Овал б) Круг в) Квадрат
- 4. Вопрос №2: Чему равна площадь основания цилиндра с радиусом 2см? а) 4π б) 8π в) 4
- 5. Вопрос №3: Как называется отрезок отмеченный красным цветом? а) диагональ цилиндра б) апофема цилиндра в)образующая цилиндра
- 6. Вопрос №4: По какой формуле можно вычислить боковую поверхность цилиндра? а) 2πRh б) 2πR(h+R) в) πR2h
- 7. Вопрос №5: По какой формуле можно вычислить полную поверхность цилиндра? а) πR2h б) 2πRh в) 2πR(h+R)
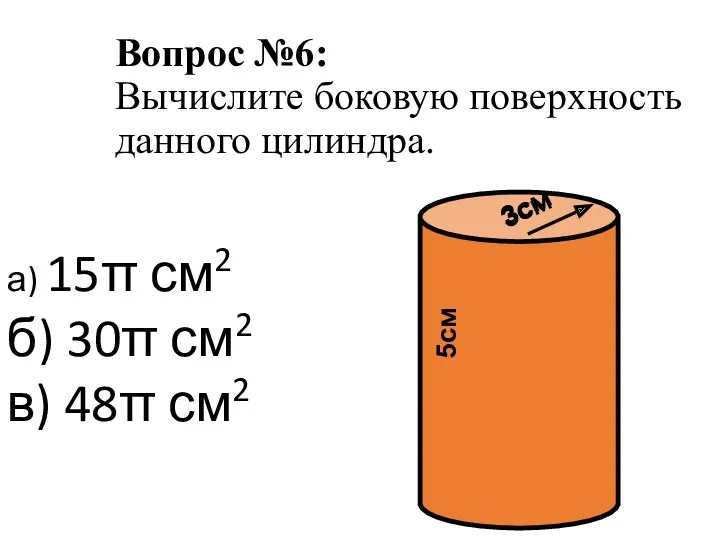
- 8. Вопрос №6: Вычислите боковую поверхность данного цилиндра. а) 15π см2 б) 30π см2 в) 48π см2
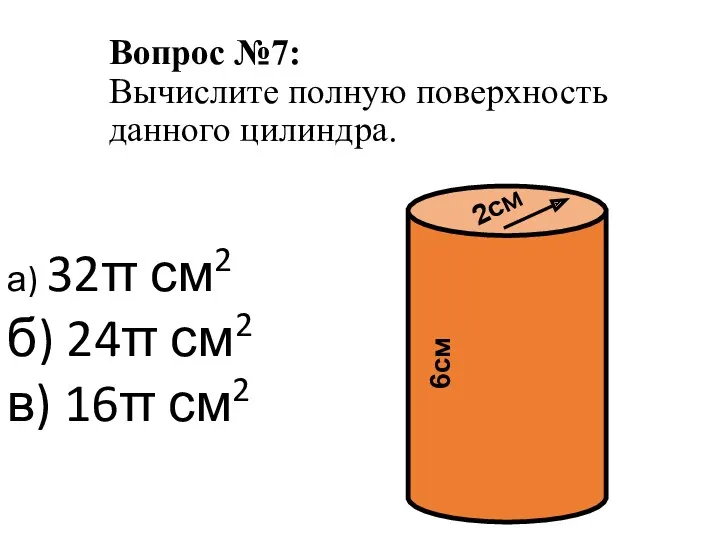
- 9. Вопрос №7: Вычислите полную поверхность данного цилиндра. а) 32π см2 б) 24π см2 в) 16π см2
- 10. Вопрос №8: Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей 3см? а) 6 см2
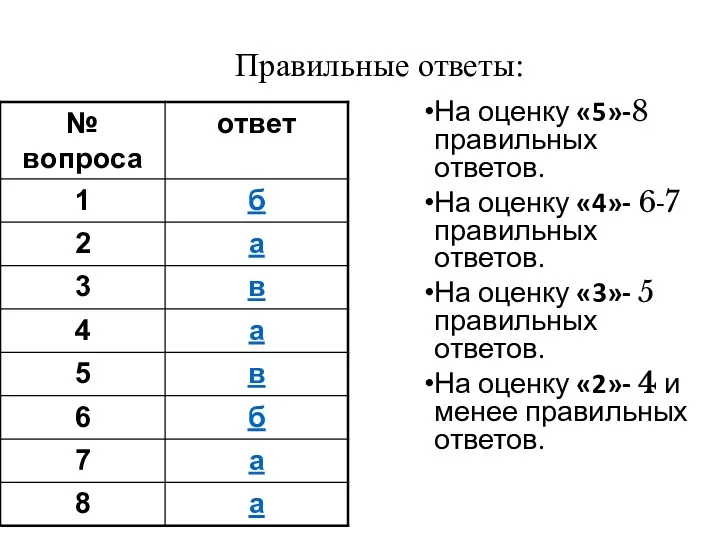
- 11. Правильные ответы: На оценку «5»-8 правильных ответов. На оценку «4»- 6-7 правильных ответов. На оценку «3»-
- 12. Тема Конус
- 13. Конус в переводе с греческого «konos» означает «сосновая шишка». Историческая справка о конусе
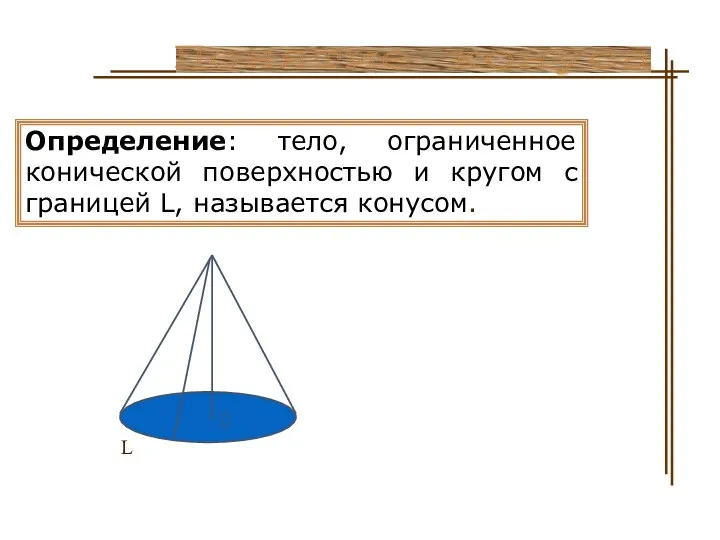
- 14. Понятие конуса Определение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. L
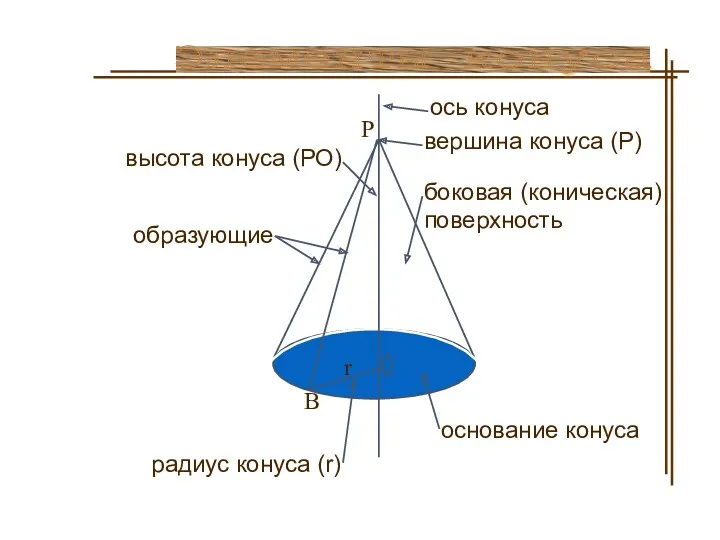
- 15. боковая (коническая) поверхность высота конуса (РО) ось конуса вершина конуса (Р) основание конуса радиус конуса (r)
- 16. Конусообраз-ные дома - трулли Оградительные конусы
- 17. Палатка
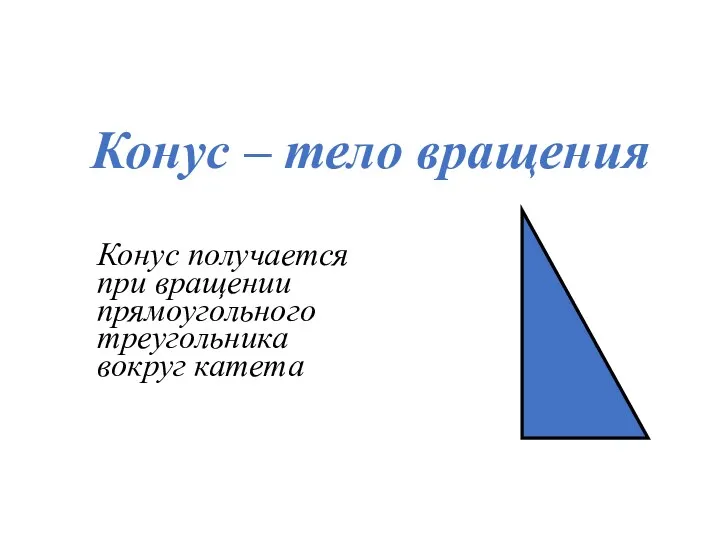
- 18. Конус – тело вращения Конус получается при вращении прямоугольного треугольника вокруг катета
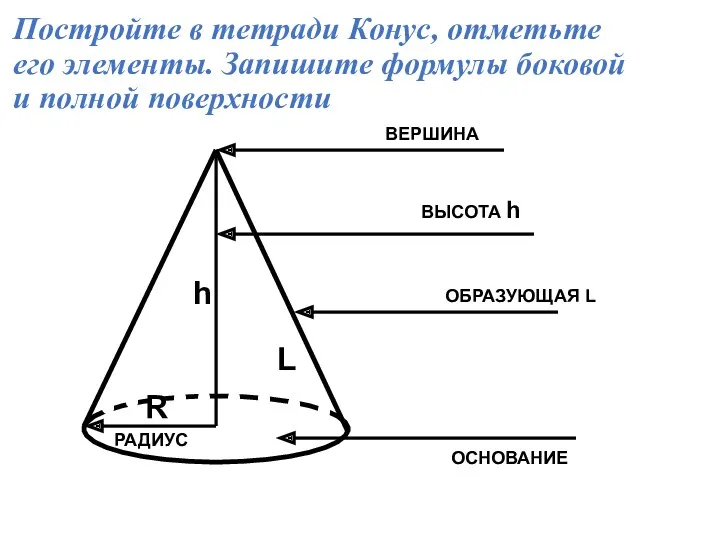
- 19. Постройте в тетради Конус, отметьте его элементы. Запишите формулы боковой и полной поверхности ОСНОВАНИЕ ВЕРШИНА ВЫСОТА
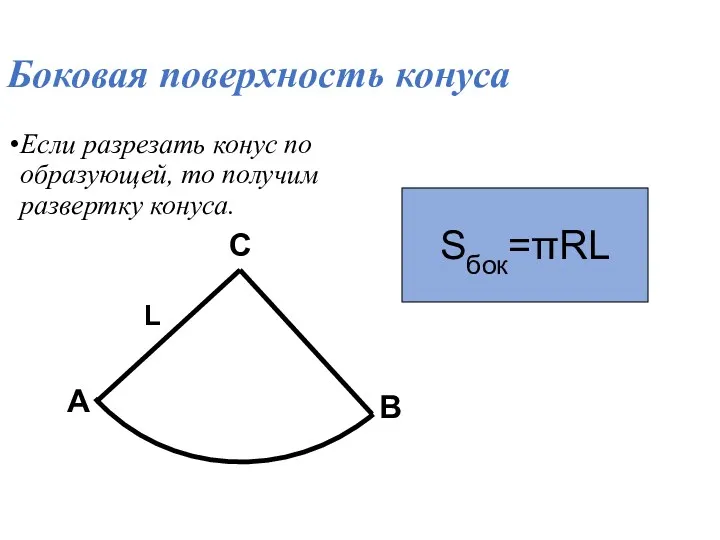
- 20. Боковая поверхность конуса Если разрезать конус по образующей, то получим развертку конуса. L A B C
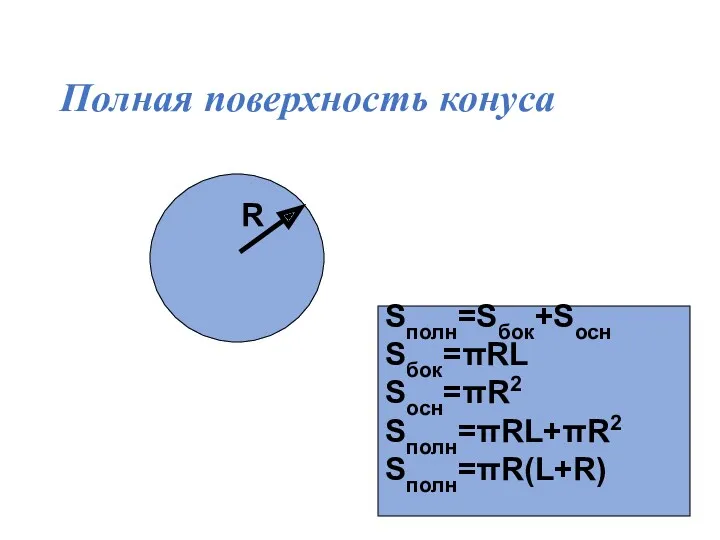
- 21. Полная поверхность конуса R Sполн=Sбок+Sосн Sбок=πRL Sосн=πR2 Sполн=πRL+πR2 Sполн=πR(L+R)
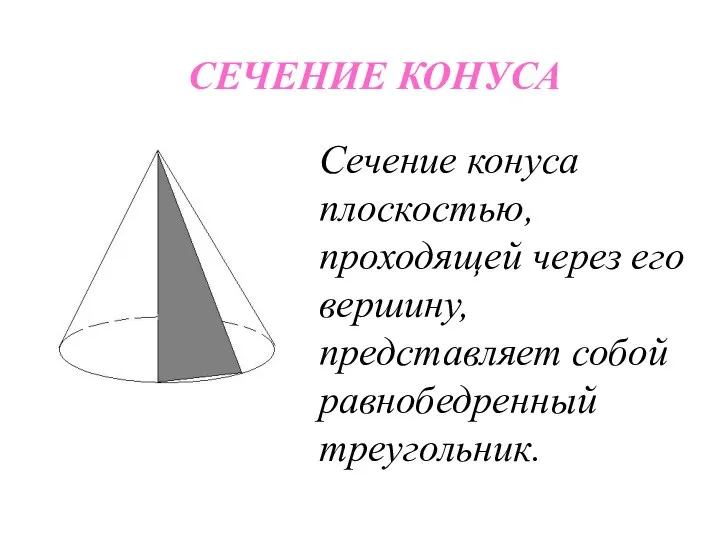
- 22. СЕЧЕНИЕ КОНУСА Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник.
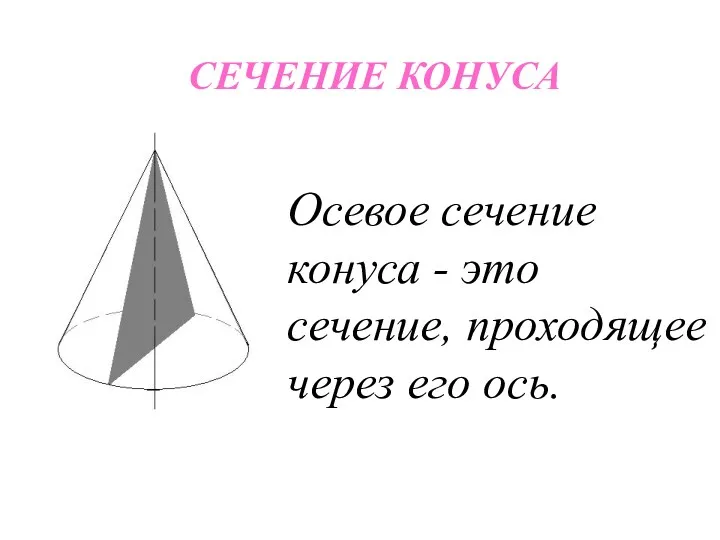
- 23. СЕЧЕНИЕ КОНУСА Осевое сечение конуса - это сечение, проходящее через его ось.
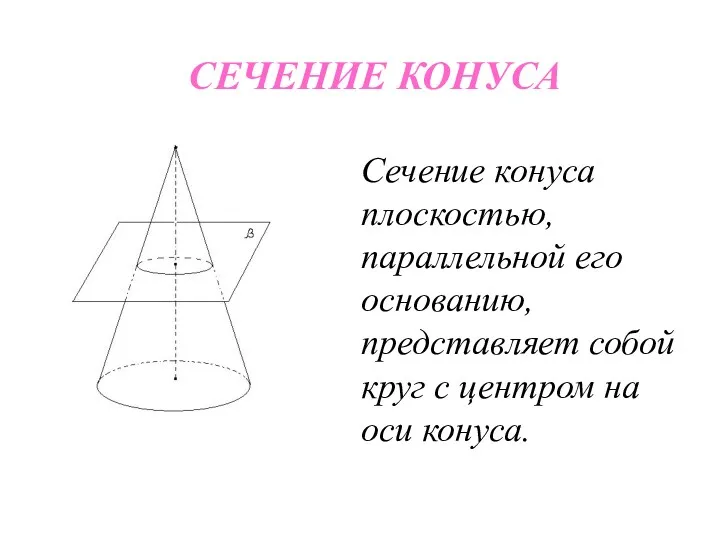
- 24. СЕЧЕНИЕ КОНУСА Сечение конуса плоскостью, параллельной его основанию, представляет собой круг с центром на оси конуса.
- 26. Скачать презентацию











 Множення на 2. Тест
Множення на 2. Тест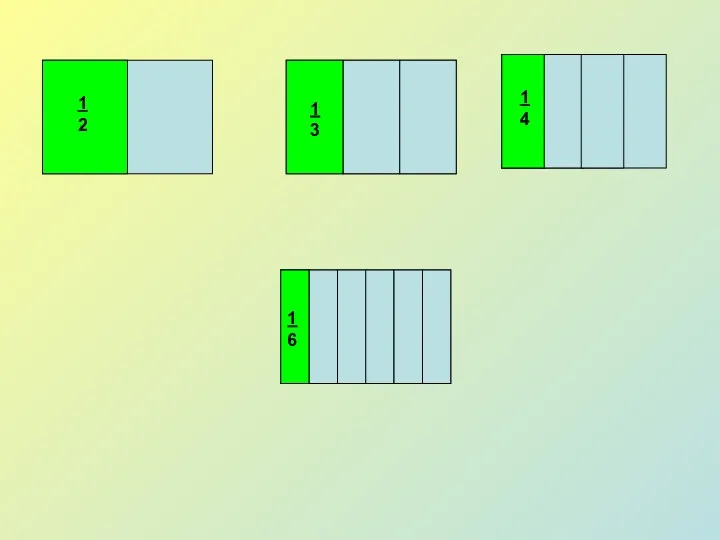 Задание по математике Сравнение долей
Задание по математике Сравнение долей Теория вероятностей и комбинаторные правила для решения задачи ЕГЭ В6
Теория вероятностей и комбинаторные правила для решения задачи ЕГЭ В6 Понятие логарифма. Свойства логарифма
Понятие логарифма. Свойства логарифма Математика - гимнастика ума
Математика - гимнастика ума Разложение многочленов на множители. Готовимся к ГИА!
Разложение многочленов на множители. Готовимся к ГИА! Презентация к конспекту урока по математике Письменные приемы сложения и вычитания двузначных чисел с переходом через десяток.
Презентация к конспекту урока по математике Письменные приемы сложения и вычитания двузначных чисел с переходом через десяток. Презентация к уроку математики во 2 классе УМК ПНШ по теме Увеличение в несколько раз
Презентация к уроку математики во 2 классе УМК ПНШ по теме Увеличение в несколько раз Часть II. Случайные величины
Часть II. Случайные величины Решение задач с величинами: цена, количество, стоимость
Решение задач с величинами: цена, количество, стоимость Модели рационального спектра. Тема 3
Модели рационального спектра. Тема 3 Ломаная линия
Ломаная линия Математическая викторина В гостях у мудрой совы
Математическая викторина В гостях у мудрой совы Drawing triangles
Drawing triangles Что такое координаты
Что такое координаты Решение задач экономического содержания
Решение задач экономического содержания Вариация. Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері
Вариация. Вариация көрсеткіштері туралы түсінік және оның міндеттері, түрлері Геометрия в начальной школе
Геометрия в начальной школе Умножение многочлена на одночлен
Умножение многочлена на одночлен Интегрированный урок во 2 классе по английскому языку и математике
Интегрированный урок во 2 классе по английскому языку и математике Прямоугольный параллелепипед. 5 класс
Прямоугольный параллелепипед. 5 класс 20230522_svoystva_trigonometricheskih_funktsiy
20230522_svoystva_trigonometricheskih_funktsiy Производные и дифференциалы высших порядков
Производные и дифференциалы высших порядков Окружность. Круг
Окружность. Круг Дифференциалы первого и высших порядков функции одной переменной. Применение дифференциала в приближенных вычислениях
Дифференциалы первого и высших порядков функции одной переменной. Применение дифференциала в приближенных вычислениях Отношения двух чисел. Урок математики в 6 классе
Отношения двух чисел. Урок математики в 6 классе Логарифмическая функция
Логарифмическая функция Урок-путешествие: Галактика- математика.
Урок-путешествие: Галактика- математика.