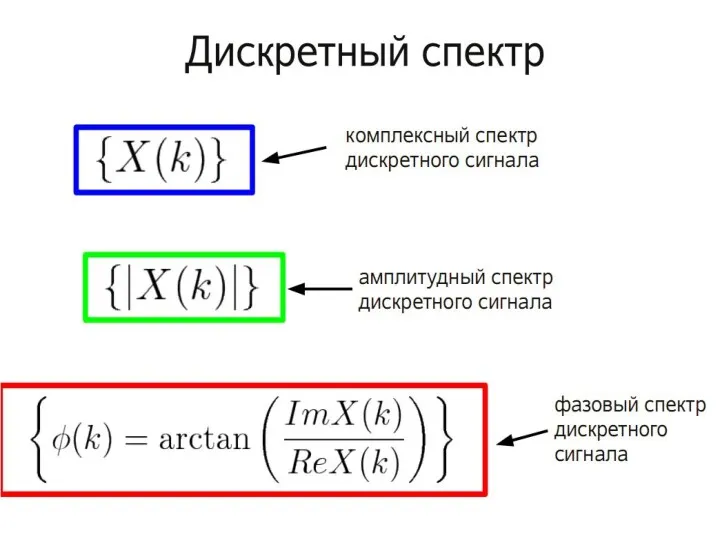
Содержание
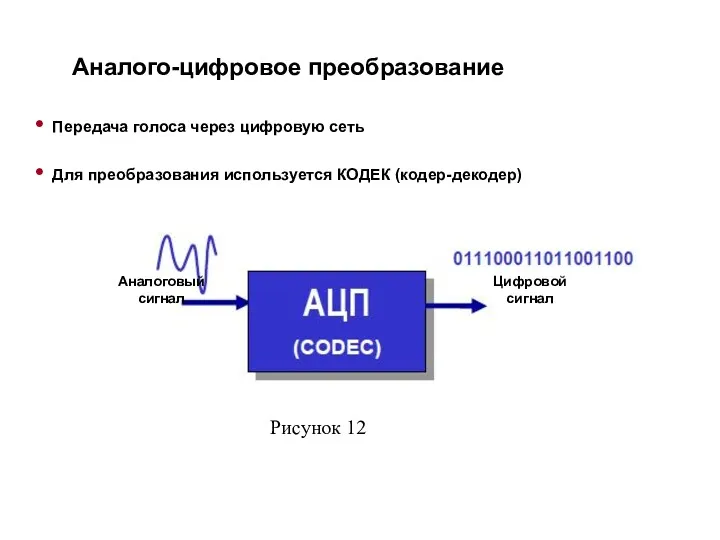
- 2. Аналого-цифровое преобразование Передача голоса через цифровую сеть Для преобразования используется КОДЕК (кодер-декодер) Аналоговый сигнал Цифровой сигнал
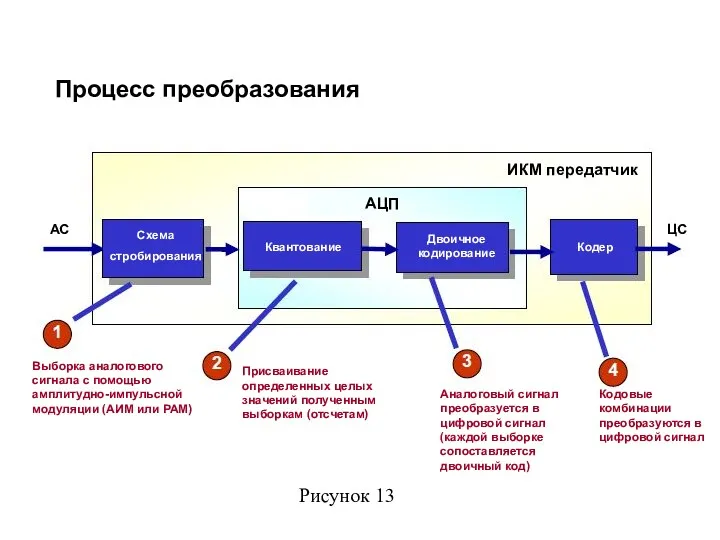
- 3. Процесс преобразования АС ИКМ передатчик АЦП ЦС Выборка аналогового сигнала с помощью амплитудно-импульсной модуляции (АИМ или
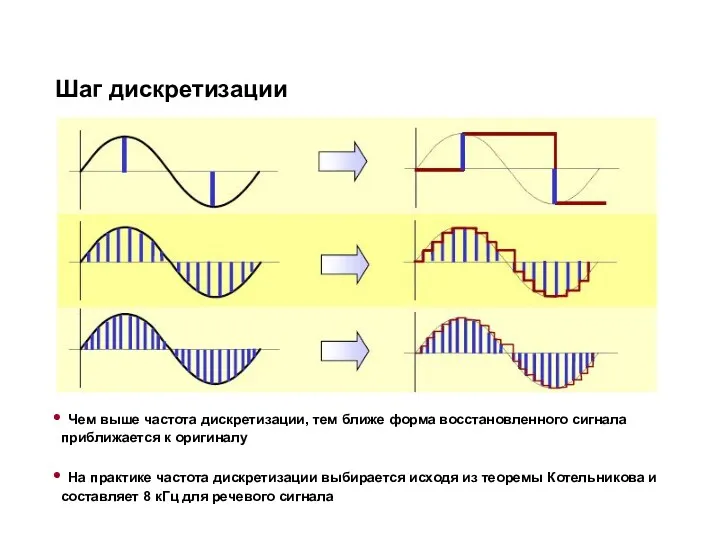
- 4. Шаг дискретизации Чем выше частота дискретизации, тем ближе форма восстановленного сигнала приближается к оригиналу На практике
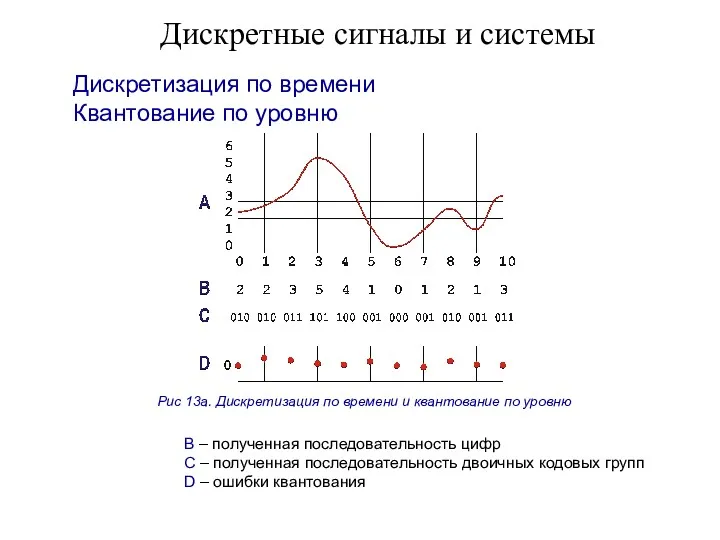
- 5. Дискретные сигналы и системы Дискретизация по времени Квантование по уровню Рис 13а. Дискретизация по времени и
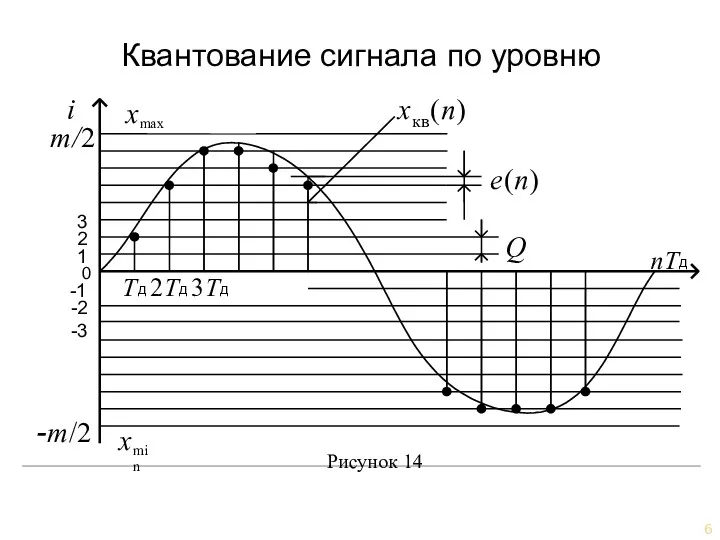
- 6. Погрешность квантования eкв(n) = хкв(n) − x(n) Квантование сигнала по уровню Рисунок 14
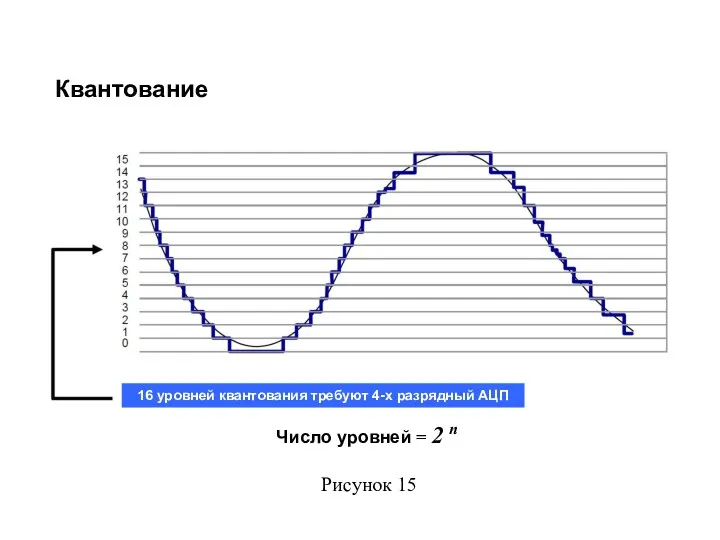
- 7. Квантование 16 уровней квантования требуют 4-х разрядный АЦП Число уровней = 2 n Рисунок 15
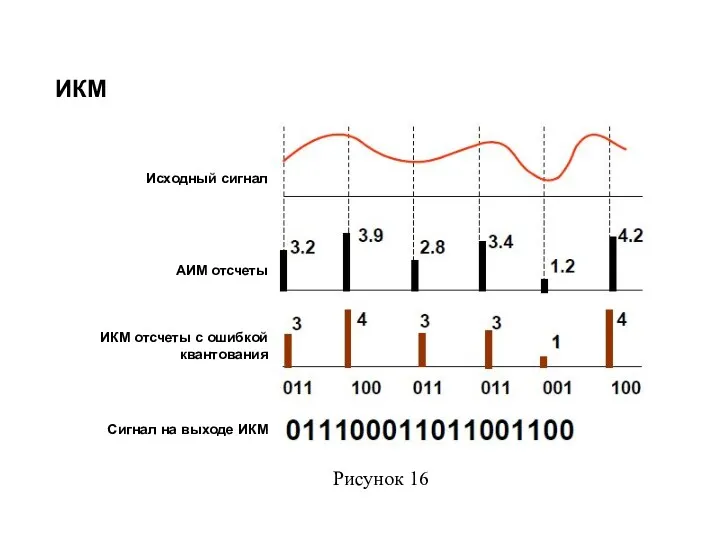
- 8. ИКМ Исходный сигнал АИМ отсчеты ИКМ отсчеты с ошибкой квантования Сигнал на выходе ИКМ Рисунок 16
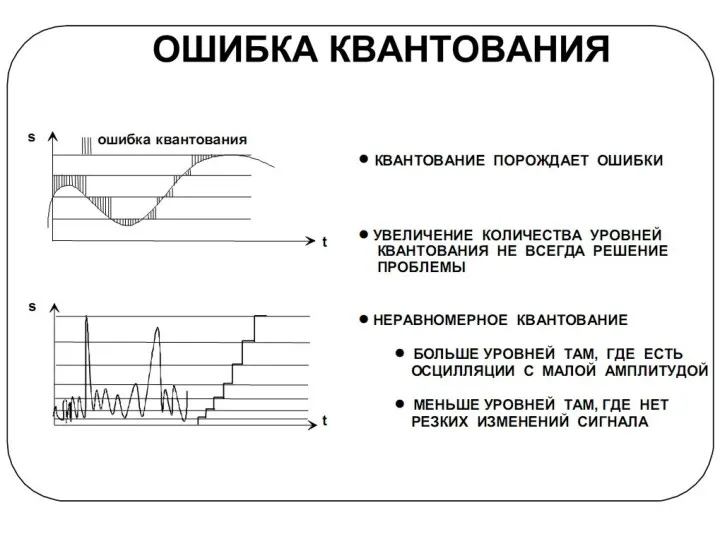
- 9. Ошибки квантования Преобразование непрерывного по уровню сигнала в цифровой - это операция квантования (quantization). Термин "квантование"
- 10. Дискретные сигналы и системы Квантование по уровню Рис 17 - Получение двоичных кодовых групп
- 12. Характеристики АЦП Динамический диапазон АЦП– это отношение максимального уровня сигнала к минимальному, с которыми может работать
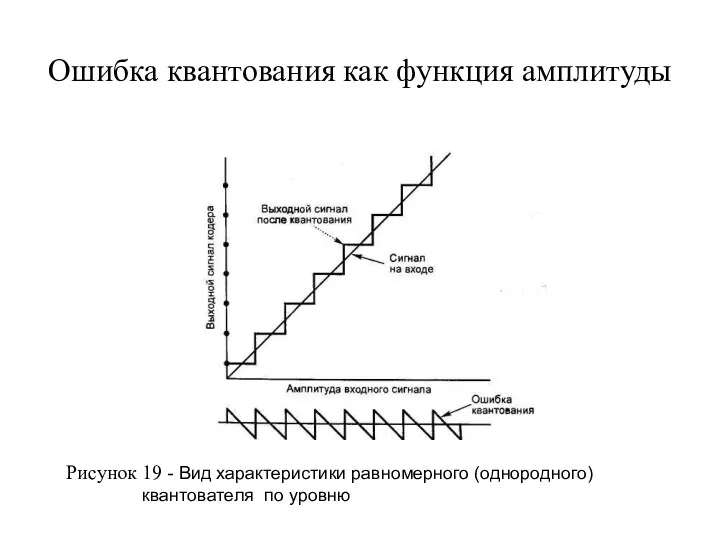
- 13. Ошибка квантования как функция амплитуды Рисунок 19 - Вид характеристики равномерного (однородного) квантователя по уровню
- 14. Ошибки квантования Обычно предполагается, что последовательные ошибки квантования в ИКМ-кодере распределены случайным образом и некоррелированы между
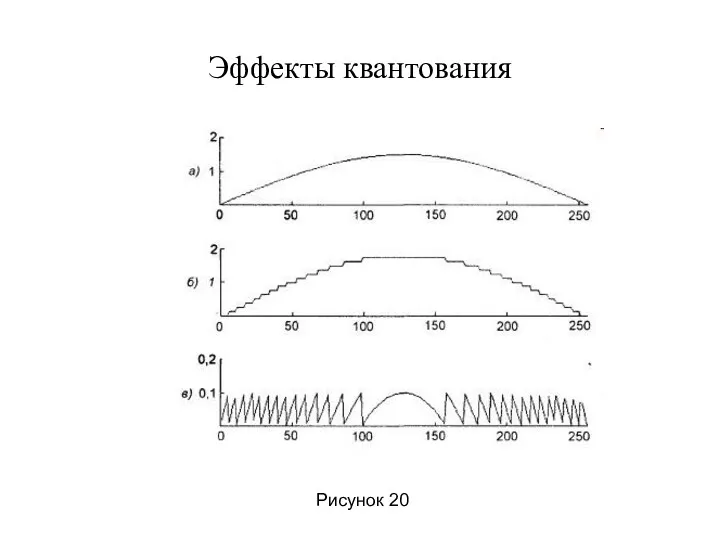
- 15. Эффекты квантования Рисунок 20
- 16. Ошибки квантования Ошибки квантования, или искажение, создаваемое дискретизацией аналогового сигнала, обычно выражается отношением средней мощности сигнала
- 17. Мощность шума квантования При определении мощности шума квантования обычно принимаютсяь три допущения: Ошибка y(t)-x(t) ограничена амплитудой
- 18. Отношение сигнал/шум Если все шаги квантования имеют равную длину (равномерное квантование) и шум квантования не зависит
- 19. Отношение сигнал/шум т.е. ≈ 6 дБ на бит. Видно, что с увеличением количества разрядов АЦП отношение
- 20. Отношение сигнал/шум Пример. Синусоидальный сигнал с амплитудой 1 В необходимо дискретизировать с минимальным значением ОСШ =
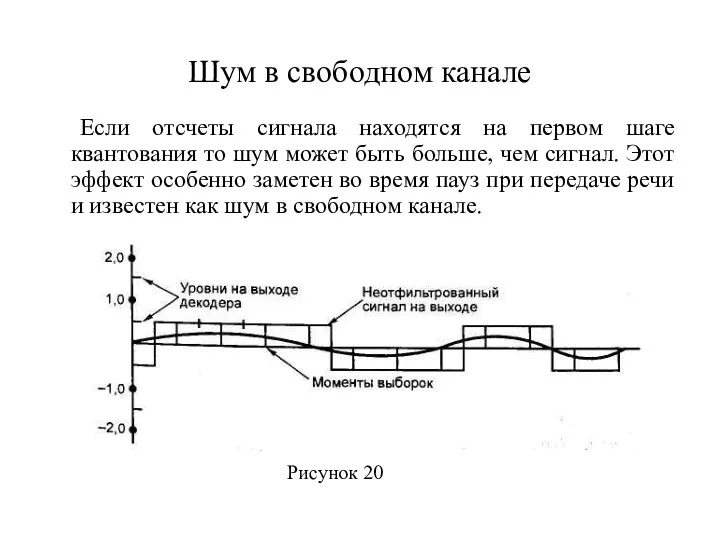
- 21. Шум в свободном канале Если отсчеты сигнала находятся на первом шаге квантования то шум может быть
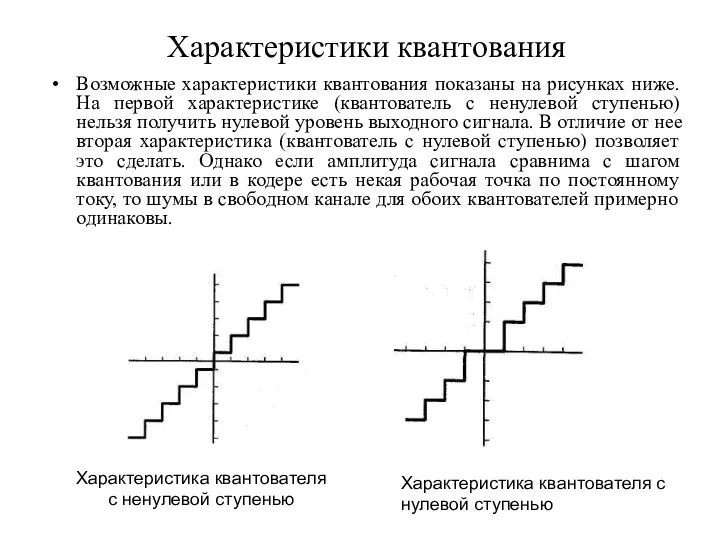
- 22. Характеристики квантования Возможные характеристики квантования показаны на рисунках ниже. На первой характеристике (квантователь с ненулевой ступенью)
- 23. ИКМ с равномерным квантованием
- 24. ИКМ с равномерным квантованием Помимо приемлемого качества для сигналов малой амплитуды, телефонная система должна быть способна
- 25. ИКМ с равномерным квантованием Характеристика системы с ИКМ и равномерным n-разрядным квантованием определяется с учетом того,
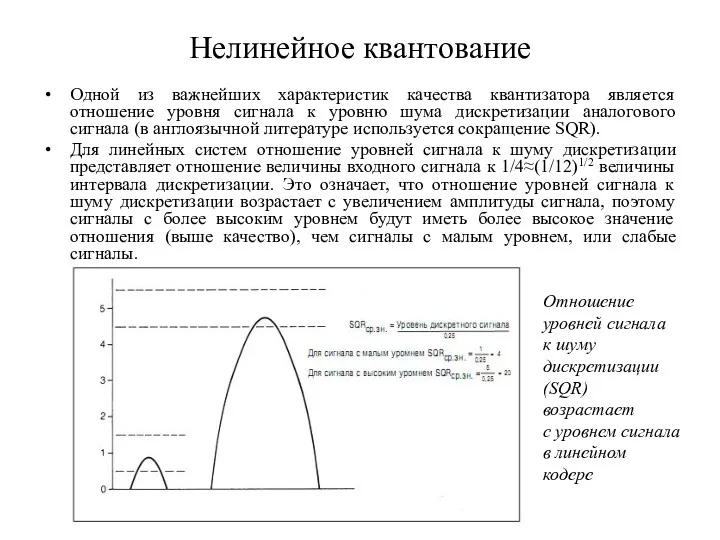
- 26. Нелинейное квантование Одной из важнейших характеристик качества квантизатора является отношение уровня сигнала к уровню шума дискретизации
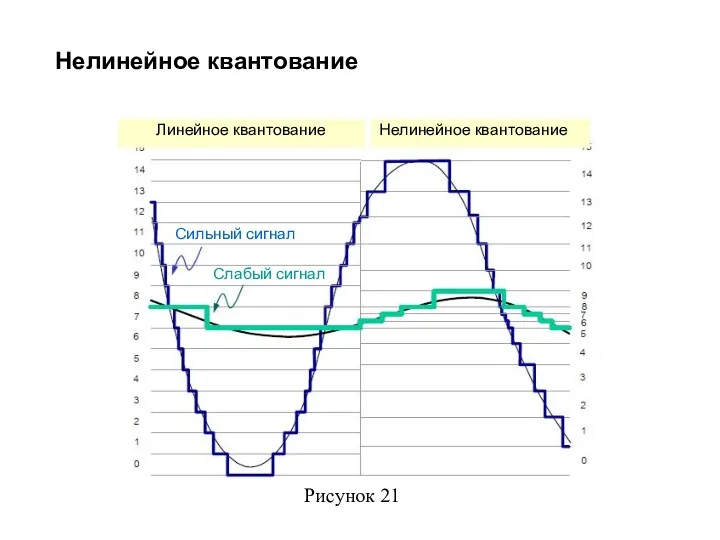
- 27. Нелинейное квантование Слабый сигнал Сильный сигнал Линейное квантование Нелинейное квантование Рисунок 21
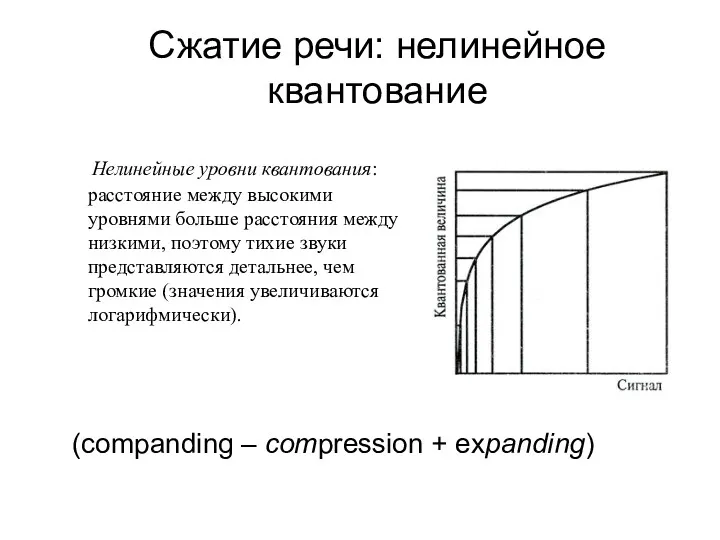
- 28. Сжатие речи: нелинейное квантование Нелинейные уровни квантования: расстояние между высокими уровнями больше расстояния между низкими, поэтому
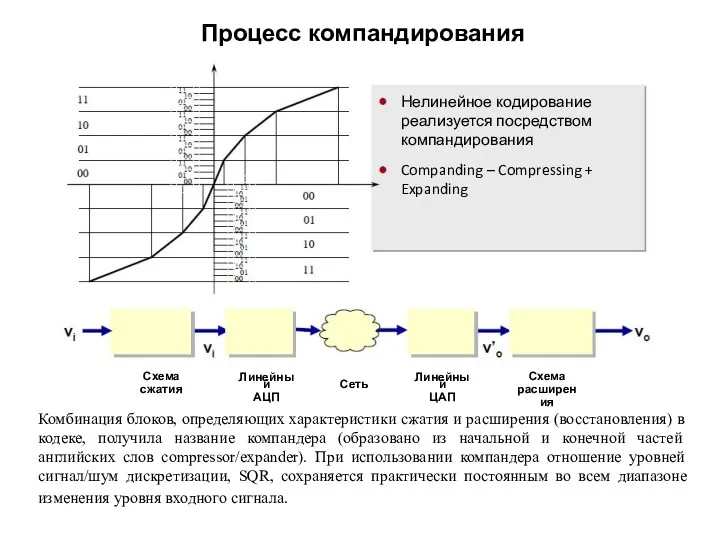
- 29. Процесс компандирования Линейный АЦП Схема сжатия Сеть Линейный ЦАП Схема расширения Нелинейное кодирование реализуется посредством компандирования
- 30. Неравномерный квантователь как совокупность компрессора, равномерного квантователя и экспандера Для уменьшения величины ошибки квантования при неизменном
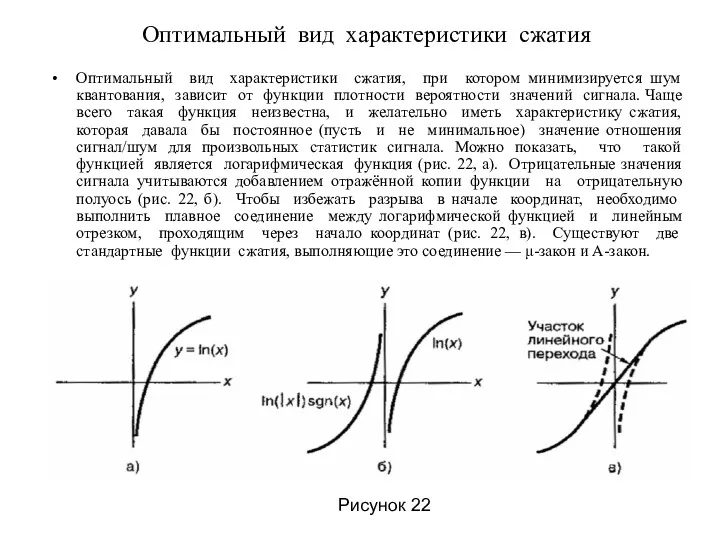
- 31. Оптимальный вид характеристики сжатия Оптимальный вид характеристики сжатия, при котором минимизируется шум квантования, зависит от функции
- 32. Стандарты компандирования μ-Закон (США, Япония) где μ = 255 (8 бит) А-Закон (Европа, Е1) где А
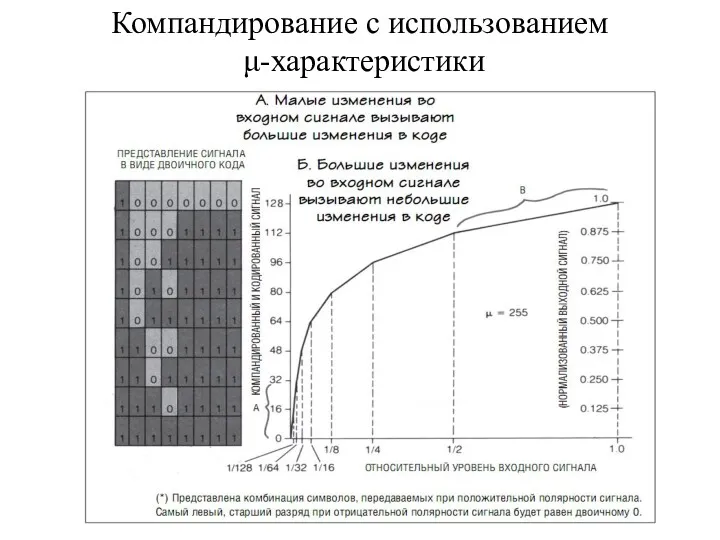
- 33. Компандирование с использованием μ-характеристики В любой цифровой сети системы связи должна быть стандартизованная схема, выполняющая компандирование
- 34. Компандирование с использованием μ-характеристики
- 35. Компандирование с использованием μ-характеристики При работе кодирующего устройства используется кусочно-линейная аппроксимация логарифмической кривой, которая представлена на
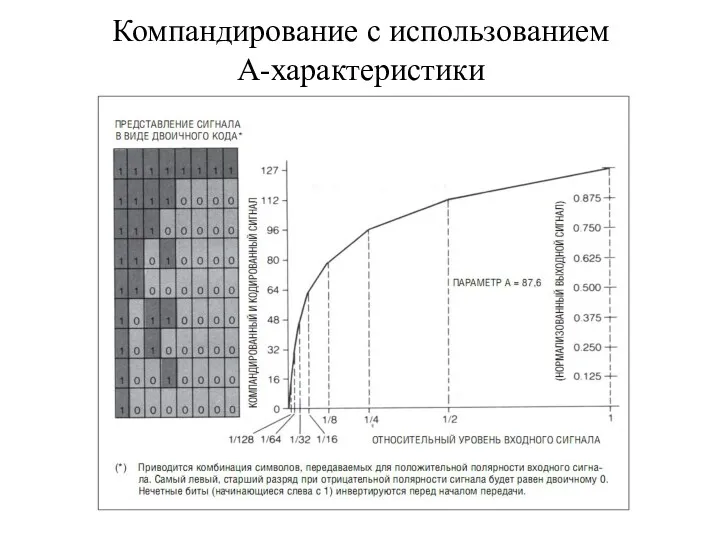
- 36. Компандирование с использованием А-характеристики Для европейских сетей стандарт компандирования определяется А-характеристикой, параметры сжатия которой определяются следующими
- 37. Компандирование с использованием А-характеристики
- 38. Компандирование с использованием А-характеристики Европейская цифровая сеть основывается на стандарте так называемой А-характеристики, которая очень схожа
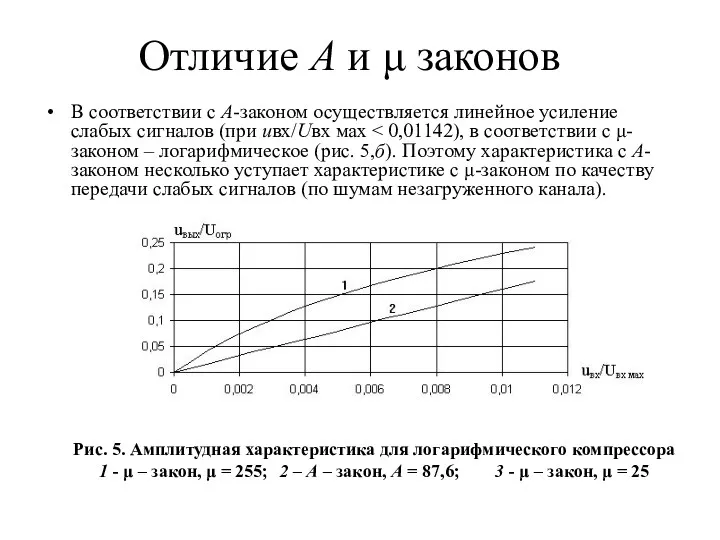
- 39. Отличие A и μ законов В соответствии с А-законом осуществляется линейное усиление слабых сигналов (при uвх/Uвх
- 40. Отличие A и μ законов
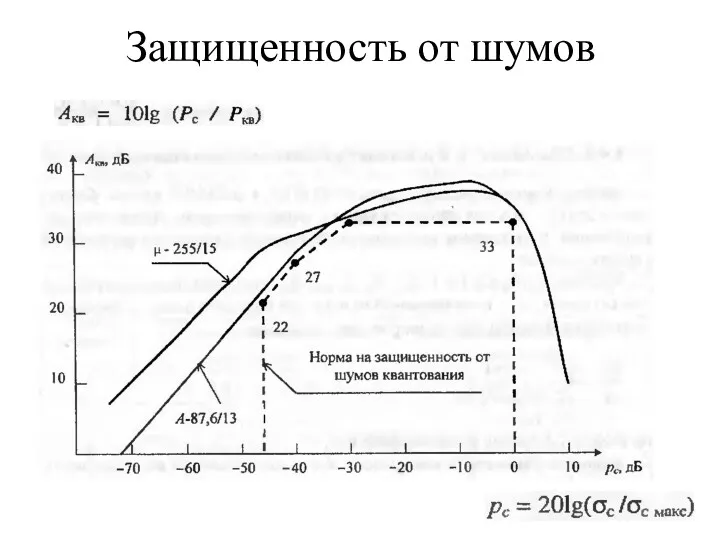
- 41. Защищенность от шумов
- 42. Цифровое компандирование Суть цифрового компандирования:
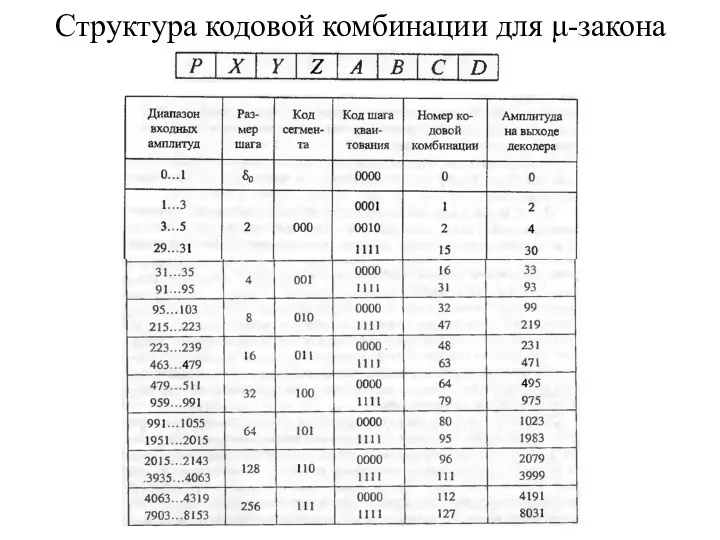
- 43. Структура кодовой комбинации для μ-закона
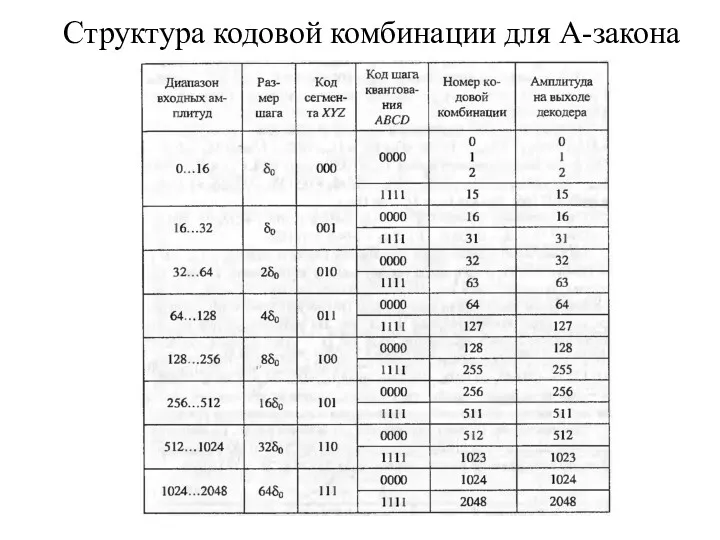
- 44. Структура кодовой комбинации для А-закона
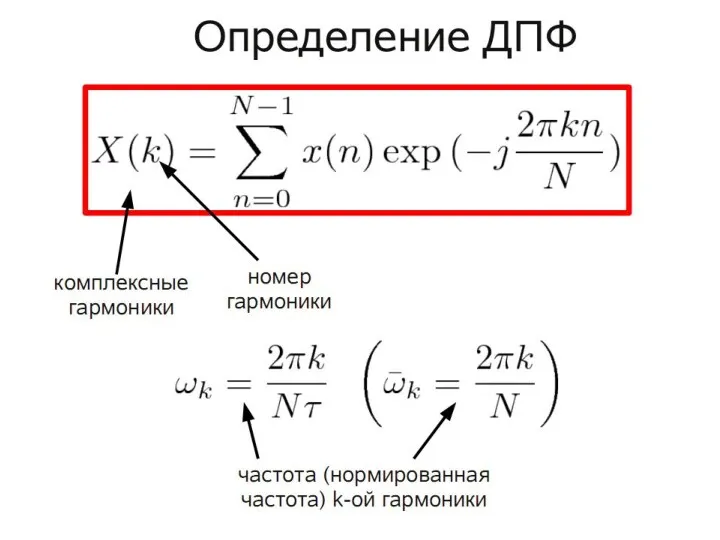
- 45. Дискретное преобразование Фурье (discrete Fourier transform, DFT) Имеем исходную последовательность N комплексных чисел (например, значения сигнала
- 46. Дискретное преобразование Фурье (discrete Fourier transform, DFT) Нормировочный множитель 1/N и знаки экспонент в DFT и
- 50. Пример ДПФ Пример: На интервале Т= [0,99], N=100, задан дискретный сигнал s(k) = δ(k-i) - прямоугольный
- 52. Свойства дискретного преобразования Фурье
- 53. Свойства дискретного преобразования Фурье
- 54. Свойства дискретного преобразования Фурье 5. Ортогональность Базовые функции образуют ортогональный набор над множеством N-мерных комплексных векторов:
- 55. 6 Теоремы Планшереля и Парсеваля Если последовательности Xk и Yk — дискретные Фурье-образы последовательностей xk и
- 56. 7 Теорема о сдвиге Умножение каждого члена исходной последовательности xk на множитель линейной фазы приводит к
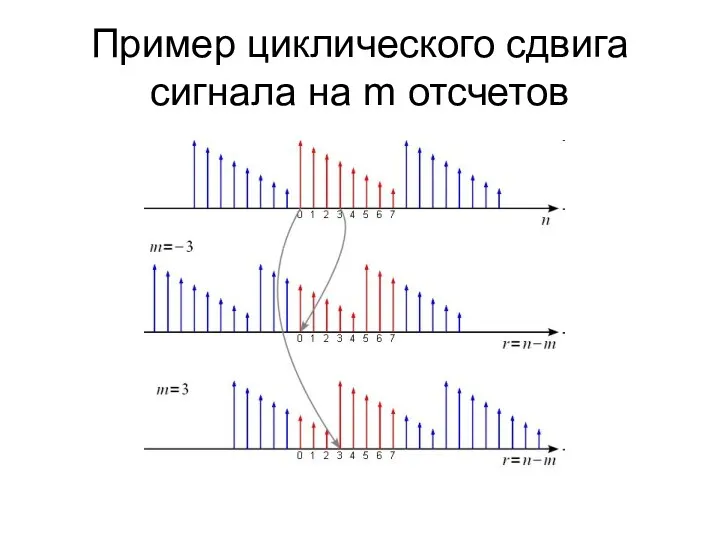
- 57. Пример циклического сдвига сигнала на m отсчетов
- 58. 8 Дуализм периодичности/дискретности во временном/частотном доменах Фурье-образ дискретной временной последовательности (гребенки Дирака с интервалом между зубцами
- 59. 9 Теоремы о циклической свертке и о взаимной корреляции Дискретный аналог свертки функций определяется формулой Последовательность
- 61. Скачать презентацию























![Пример ДПФ Пример: На интервале Т= [0,99], N=100, задан дискретный](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/16739/slide-49.jpg)








 ОГЭ по математике в 2018 году
ОГЭ по математике в 2018 году Движение. Преобразование фигур
Движение. Преобразование фигур Примеры способов определения понятий в математике в начальной школе
Примеры способов определения понятий в математике в начальной школе 7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар
7, 8, 0 цифрларын пайдалана отырып, барынша үш таңбалы сандарды жазыңдар Неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Лекция 2.11)
Неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами. (Лекция 2.11) Компьютерная дидактическая игра на понятие Много - один для детей 2-ой младшей группы.
Компьютерная дидактическая игра на понятие Много - один для детей 2-ой младшей группы. Координатная плоскость
Координатная плоскость Презентация Что такое умножение.
Презентация Что такое умножение. Функция. График функции
Функция. График функции Единицы измерения площадей
Единицы измерения площадей Таблица сложения. Повторение
Таблица сложения. Повторение презентация к уроку математики 2 класс
презентация к уроку математики 2 класс Устный счет. Решите задачи. 1 класс
Устный счет. Решите задачи. 1 класс Реши ребус – отгадай слово
Реши ребус – отгадай слово Умножение и деление на 10
Умножение и деление на 10 Площадь фигуры.
Площадь фигуры. Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Площади. Формула площади прямоугольника
Площади. Формула площади прямоугольника Устный счет
Устный счет Определенный интеграл
Определенный интеграл Логарифмическая функция
Логарифмическая функция Средние величины и показатели вариации. (Занятие 7)
Средние величины и показатели вариации. (Занятие 7) Объемы тел
Объемы тел Цилиндр
Цилиндр Методы проецирования. Проекции точки, проекции прямой (1 лекция)
Методы проецирования. Проекции точки, проекции прямой (1 лекция) Графический способ решения систем уравнений
Графический способ решения систем уравнений Интерактивный тест Во сколько раз больше, меньше
Интерактивный тест Во сколько раз больше, меньше Разложение квадратного трёхчлена на множители
Разложение квадратного трёхчлена на множители