Содержание
- 2. OVERVIEW Application of matrices SLEs Kronecker-Cappelli Theorem.
- 3. 2- APPLICATION OF MATRICES Graph theory Computer graphics Cryptography Solving SLEs
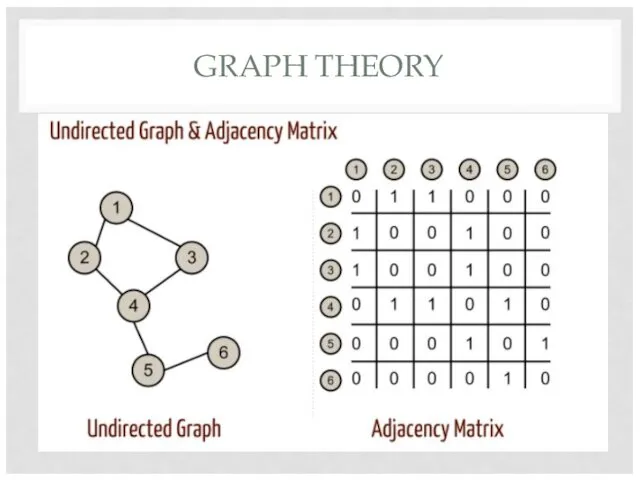
- 4. GRAPH THEORY
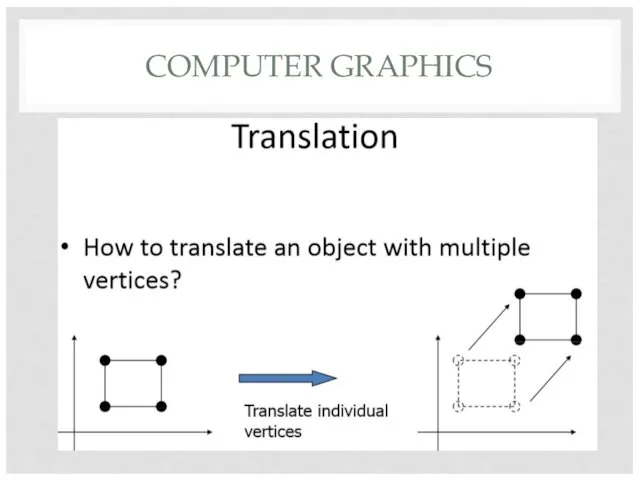
- 5. COMPUTER GRAPHICS
- 6. COMPUTER GRAPHICS
- 7. COMPUTER GRAPHICS
- 8. CRYPTOGRAPHY Study of encoding and decoding secret messages Useful in sending sensitive information so that only
- 9. A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8
- 10. Encoding matrix Plaintext Ciphertext Encrypting the Message x =
- 11. DECIPHERING THE MESSAGE In order to decode the message, we would have to take the inverse
- 12. A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8
- 13. A 1 B 2 C 3 D 4 E 5 F 6 G 7 H 8
- 14. 2- SOLVING SLES
- 15. KRONECKER-CAPPELLI THEOREM Kronecker-Cappelli Theorem. A linear system has solutions if and only if the rank of
- 16. © 2010 Pearson Education, Inc. All rights reserved. Section 8.1, Slide Systems of Linear Equations Graphing
- 17. © 2010 Pearson Education, Inc. All rights reserved. Section 8.1, Slide Systems of Linear Equations Case
- 18. © 2010 Pearson Education, Inc. All rights reserved. Section 8.1, Slide Systems of Linear Equations Case
- 20. Скачать презентацию















 Величины. Таблица единиц площади.
Величины. Таблица единиц площади. Обратные действия. Увеличение и уменьшение числа
Обратные действия. Увеличение и уменьшение числа Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Площади плоских фигур и поверхности тел
Площади плоских фигур и поверхности тел Деление на группы по несколько предметов.
Деление на группы по несколько предметов. Умножение и деление на 3.
Умножение и деление на 3. Решение задач по теме Площади фигур
Решение задач по теме Площади фигур Свойства сложения натуральных чисел. Урок математики в 5 классе
Свойства сложения натуральных чисел. Урок математики в 5 классе Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Роль и место математики в мире и медицине
Роль и место математики в мире и медицине Урок - сказка по математике
Урок - сказка по математике Волшебные часы
Волшебные часы Решение тригонометрических неравенств
Решение тригонометрических неравенств Развитие функционально-графического мышления учащихся при изучении алгебры 7-9 класс
Развитие функционально-графического мышления учащихся при изучении алгебры 7-9 класс Элементы математической статистики
Элементы математической статистики Геометрические фигуры.
Геометрические фигуры. Презентация практических достижений профессиональной деятельности по образовательной области Познавательное развитие
Презентация практических достижений профессиональной деятельности по образовательной области Познавательное развитие Неравенства и системы неравенств с двумя переменными
Неравенства и системы неравенств с двумя переменными Системы уравнений с несколькими неизвестными. Метод замены неизвестных
Системы уравнений с несколькими неизвестными. Метод замены неизвестных Логарифмы в природе
Логарифмы в природе Линейная алгебра
Линейная алгебра Системы уравнений с двумя переменными (9 класс)
Системы уравнений с двумя переменными (9 класс) Презентация по математике по теме Вычитание чисел 6,7,8,9. Освоение приема вида□ – 6; □ – 7; □ – 8; □ – 9.
Презентация по математике по теме Вычитание чисел 6,7,8,9. Освоение приема вида□ – 6; □ – 7; □ – 8; □ – 9. Презентация Занимательная математика
Презентация Занимательная математика Функція = + bx + c, її властивості та графік
Функція = + bx + c, її властивості та графік Математическая игра Думай, считай, отгадывай
Математическая игра Думай, считай, отгадывай Центральная и осевая симметрия
Центральная и осевая симметрия Построение графика квадратичной функции
Построение графика квадратичной функции