Содержание
- 2. РАЗДЕЛ 1. ЛИНЕЙНАЯ АЛГЕБРА. Линейная алгебра является необходимым инструментарием для компактного и эффективного описания и анализа
- 3. ТЕМА 1. МАТРИЦЫ Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеет
- 4. Матрицу А называют матрицей размера и пишут Числа , составляющие матрицу, называется ее элементами. Элементы, стоящие
- 5. Виды матриц Если количество строк равно количеству столбцов, т.е. m=n, то матрица называется квадратной. Квадратную матрицу
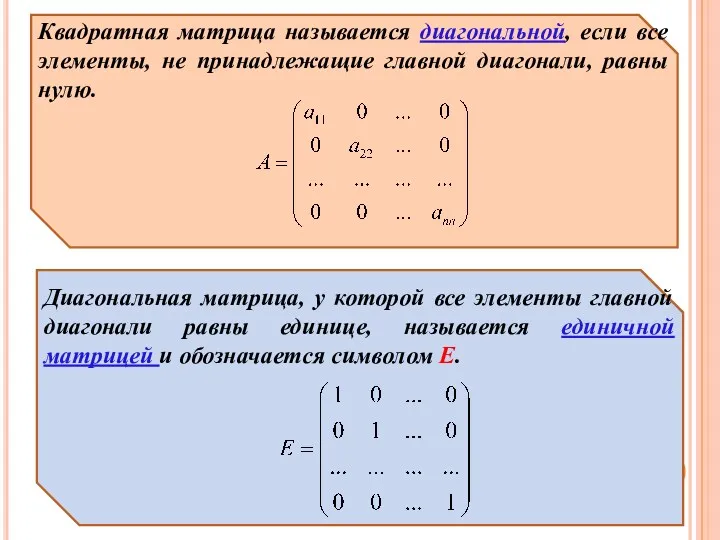
- 6. Квадратная матрица называется диагональной, если все элементы, не принадлежащие главной диагонали, равны нулю. Диагональная матрица, у
- 7. Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
- 8. Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
- 9. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной
- 10. Действия над матрицами Операция сложения матриц вводится только для матриц одинаковых размеров. Суммой двух матриц и
- 11. Пример сложения и вычитания матриц Даны матрицы: Сумма матриц: Разность матриц:
- 12. Умножение на число Произведением матрицы на число k называется матрица такая, что Записывают B=k⋅A. Пример: Матрица
- 13. Операции сложения, вычитания и умножения матрицы на число обладают следующими свойствами: А + В = В
- 14. Элементарные преобразования матриц Элементарными преобразованиями матриц являются: перестановка местами двух параллельных рядов матрицы; умножение всех элементов
- 15. ПРИМЕР: ПРИВЕСТИ К КАНОНИЧЕСКОМУ ВИДУ МАТРИЦУ Решение: выполняя элементарные преобразования, получаем:
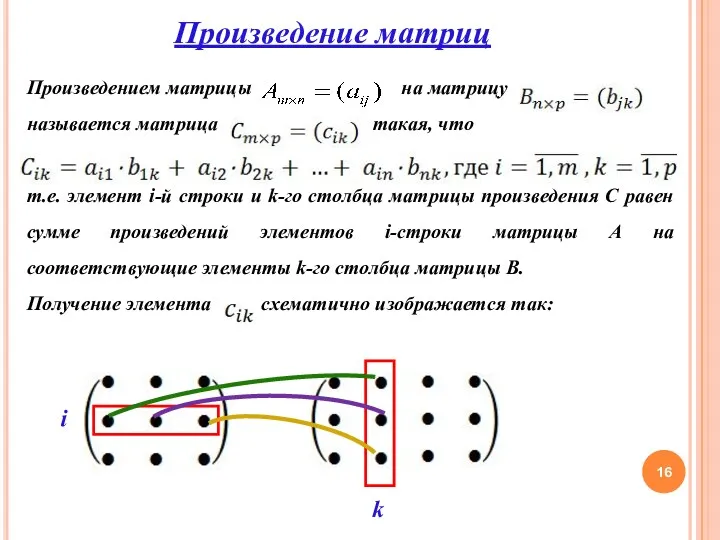
- 16. Произведение матриц Произведением матрицы на матрицу называется матрица такая, что т.е. элемент i-й строки и k-го
- 17. Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко
- 18. Пример: . Тогда произведение А⋅ В не определено, так как число столбцов матрицы А не совпадает
- 19. Если, конечно, написанные суммы и произведения матриц имеют смысл. Для операции транспонирования верны свойства: (А +
- 20. Тема 2. Определители Квадратной матрице А порядка n можно сопоставить число det A (или |А|, или
- 21. Вычисление определителя 2-го порядка, иллюстрируется схемой:
- 22. Примеры:
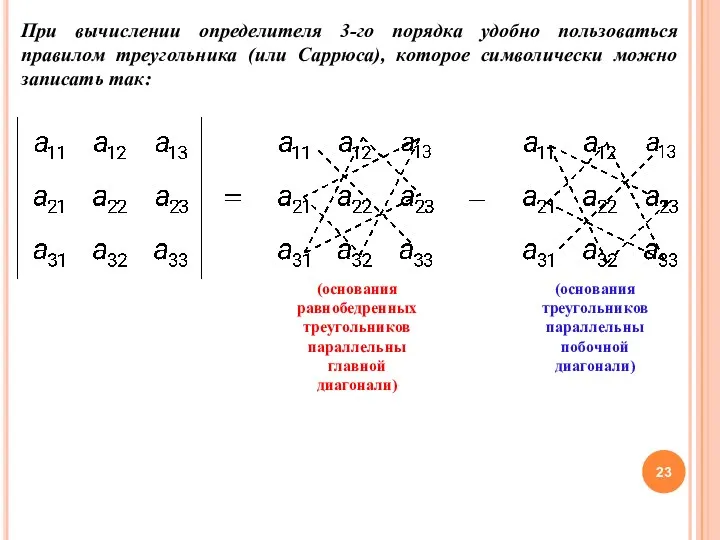
- 23. При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника (или Саррюса), которое символически можно записать так:
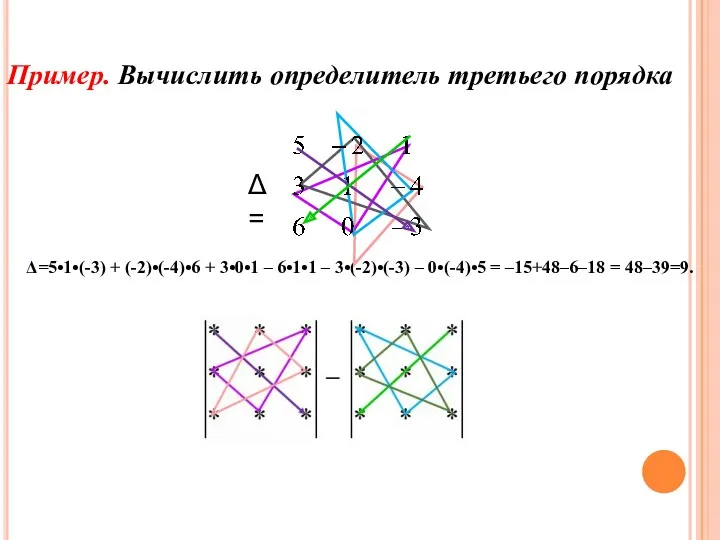
- 24. Пример. Вычислить определитель третьего порядка Δ=5•1•(-3) + (-2)•(-4)•6 + 3•0•1 – 6•1•1 – 3•(-2)•(-3) – 0•(-4)•5
- 25. Пример. Вычислить определитель с помощью правила диагоналей - - - + + + Δ=5•1•(-3) + (-2)•(-4)•6
- 26. 1. Определитель не изменится, если его транспонировать: Тема 2.2 Свойства определителей
- 27. 2. При перестановке двух строк или столбцов определитель изменит свой знак на противоположный.
- 28. 3. Определитель с двумя одинаковыми строками или столбцами равен нулю.
- 29. 4. Общий множитель всех элементов строки или столбца можно вынести за знак определителя.
- 30. Пример:
- 31. 5. Если все элементы двух строк (или столбцов) определителя пропорциональны, то определитель равен нулю.
- 32. 6. Если каждый элемент какого-либо ряда определителя представляет собой сумму двух слагаемых, то такой определитель равен
- 34. 7. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца) ,
- 35. ×2 +
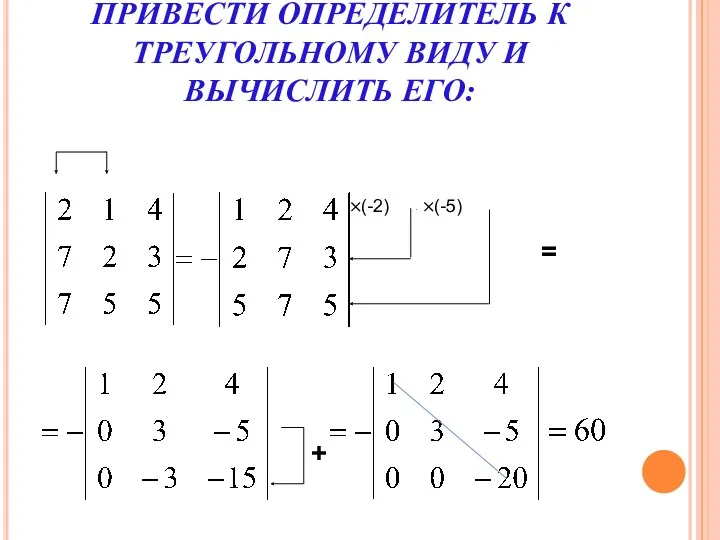
- 36. 8. Треугольный определитель равен произведению элементов главной диагонали.
- 37. ПРИВЕСТИ ОПРЕДЕЛИТЕЛЬ К ТРЕУГОЛЬНОМУ ВИДУ И ВЫЧИСЛИТЬ ЕГО: ×(-2) ×(-5) = +
- 38. РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО ЭЛЕМЕНТАМ СТРОКИ ИЛИ СТОЛБЦА. Минором элемента det D называется такой новый определитель, который
- 40. Алгебраическим дополнением Aij элемента aij det D называется минор Mij этого элемента, взятый со знаком т.е.
- 42. Сумма произведений элементов любой строки (или столбца) определителя на их алгебраические дополнения равна этому определителю. Теорема:
- 43. разложение по i-ой строке: разложение по j-му столбцу:
- 44. РАЗЛОЖИТЬ ДАННЫЙ ОПРЕДЕЛИТЕЛЬ ПО ЭЛЕМЕНТАМ: 1) 3-ЕЙ СТРОКИ; 2) 1-ГО СТОЛБЦА.
- 45. 1) РАЗЛОЖИМ ДАННЫЙ ОПРЕДЕЛИТЕЛЬ ПО ЭЛЕМЕНТАМ 3-ЕЙ СТРОКИ:
- 47. 2) РАЗЛОЖИМ ДАННЫЙ ОПРЕДЕЛИТЕЛЬ ПО ЭЛЕМЕНТАМ 1-ГО СТОЛБЦА:
- 49. ОСНОВНЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ. 1. разложение определителя по элементам строки или столбца; 2. метод эффективного понижения
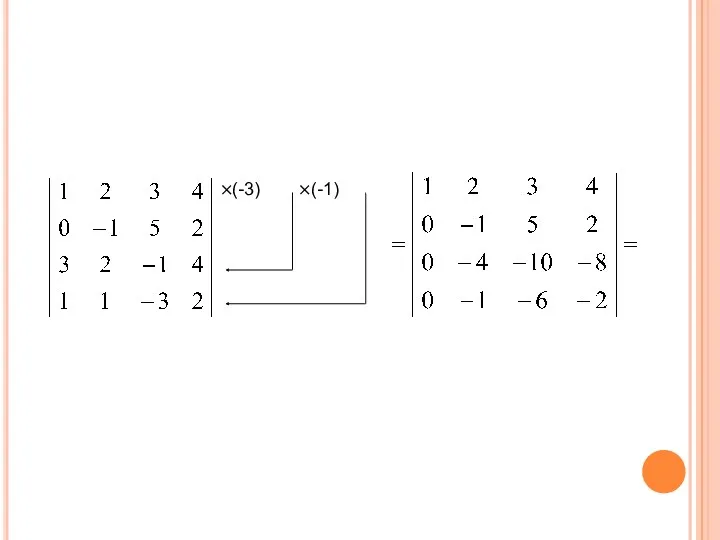
- 50. Метод эффективного понижения порядка: Вычисление определителя n-го порядка сводится к вычислению одного определителя (n-1)-го порядка, сделав
- 51. ×(-3) ×(-1)
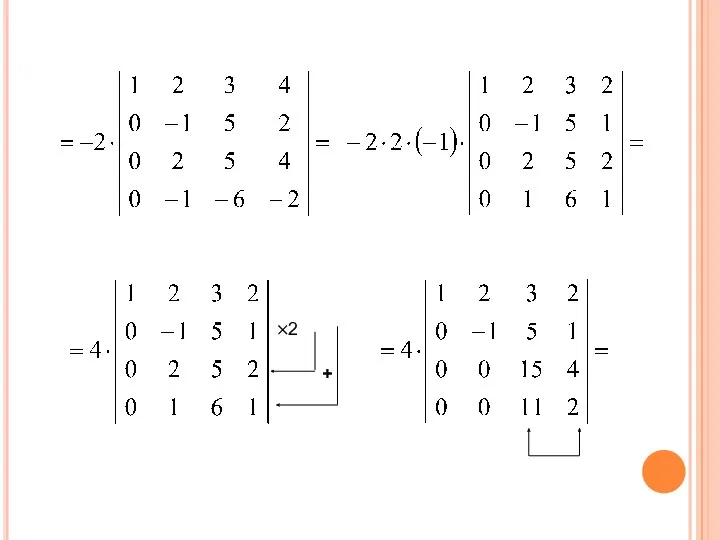
- 53. ВЫЧИСЛИТЬ ОПРЕДЕЛИТЕЛЬ ПРИВЕДЕНИЕМ ЕГО К ТРЕУГОЛЬНОМУ ВИДУ. ×(-3) ×(-1)
- 54. ×2 +
- 55. ×(-2)
- 56. ТЕМА 3. ОБРАТНАЯ МАТРИЦА
- 57. Квадратная матрица порядка n называется невырожденной, если её определитель не равен нулю. В противном случае (detA=0)
- 58. Если А- квадратная матрица, то обратной по отношению к матрице А называется матрица, которая будучи умноженной
- 59. Если обратная матрица существует, то матрица А называется обратимой. Операция вычисления обратной матрицы при условии, что
- 60. Теорема. Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была
- 61. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ: где присоединенная матрица
- 62. ЧТОБЫ НАЙТИ ОБРАТНУЮ МАТРИЦУ: 1. находят det A и убеждаются, что det A ≠ 0; 2.
- 63. Пример 1. Найти матрицу, обратную к матрице А:
- 64. 1) НАХОДИМ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ А:
- 65. 2) НАХОДИМ АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ ВСЕХ ЭЛЕМЕНТОВ МАТРИЦЫ А:
- 67. ЗАПИСЫВАЕМ НОВУЮ МАТРИЦУ: 3) транспонируем эту матрицу:
- 68. 4) УМНОЖИМ ПОЛУЧЕННУЮ МАТРИЦУ НА
- 69. ПРОВЕРКА: Ответ:
- 70. РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ.
- 71. Пример 2. Найти матрицу Х:
- 72. Пример 3. Найти матрицу Х: А В
- 76. Проверка:
- 77. Ответ:
- 78. Пример 4. Показать, что
- 80. Скачать презентацию





























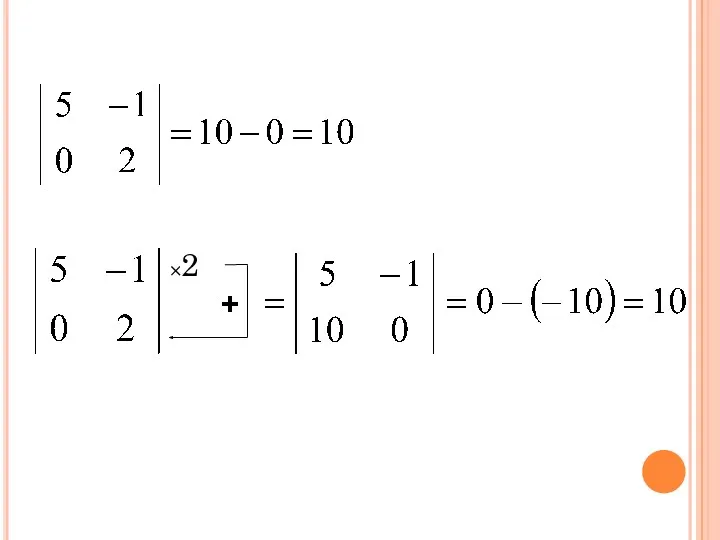


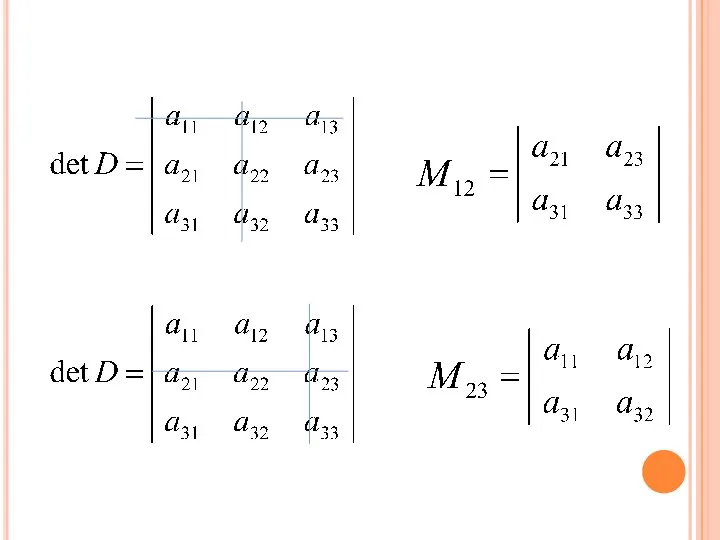

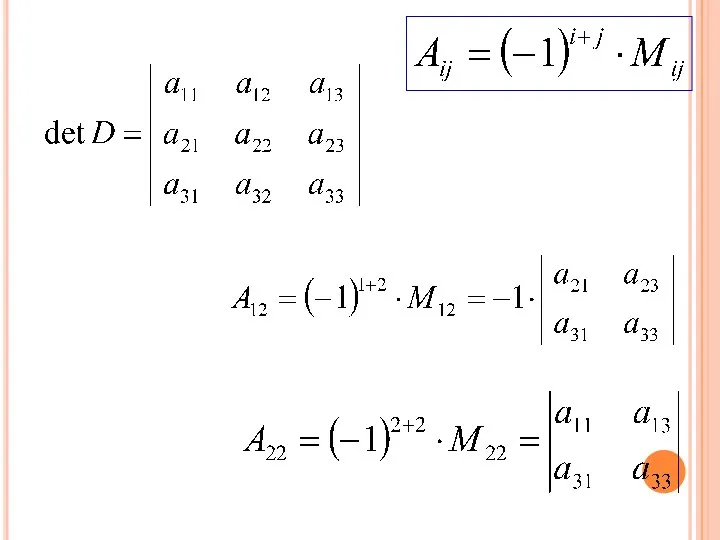

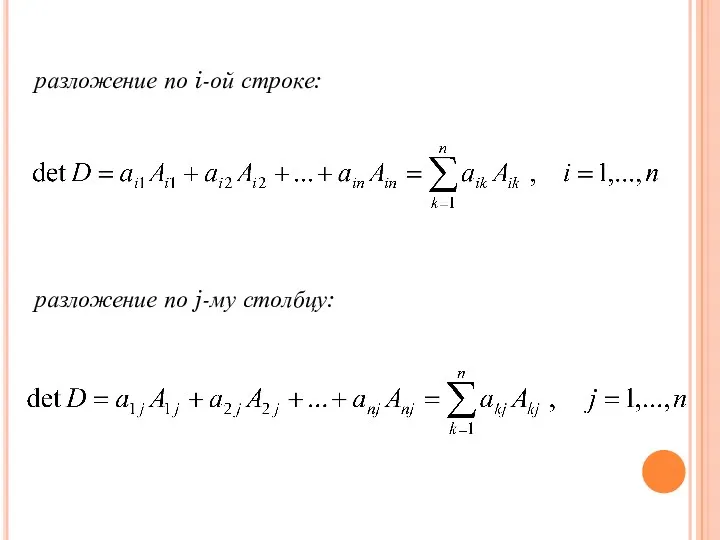


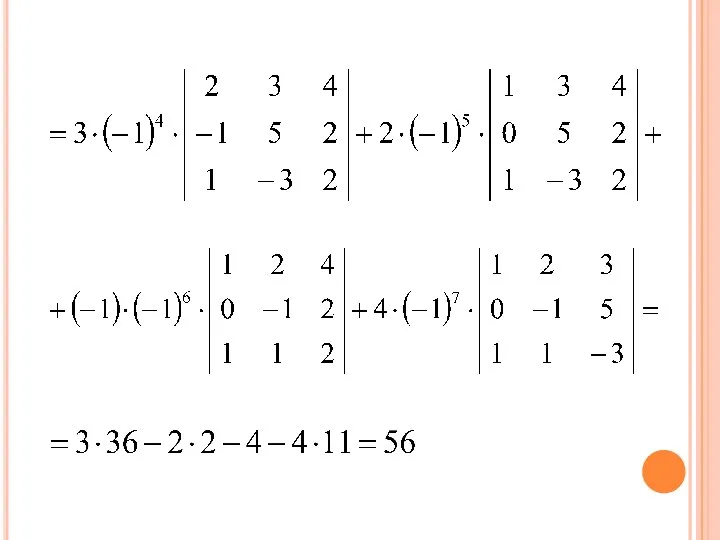

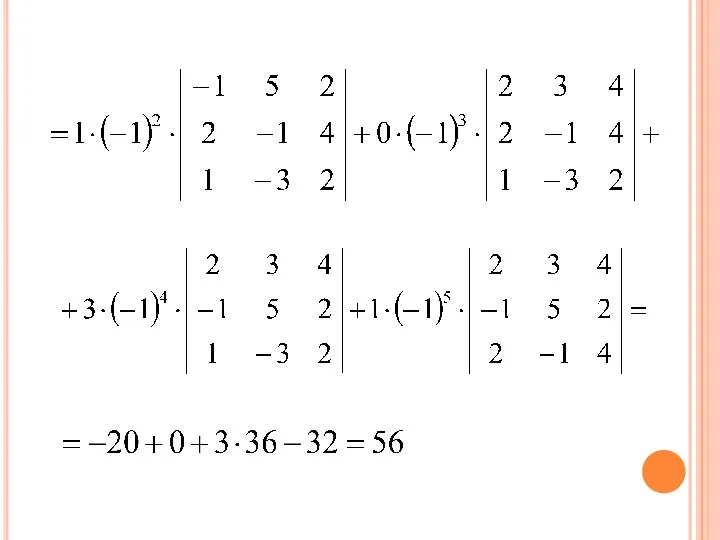


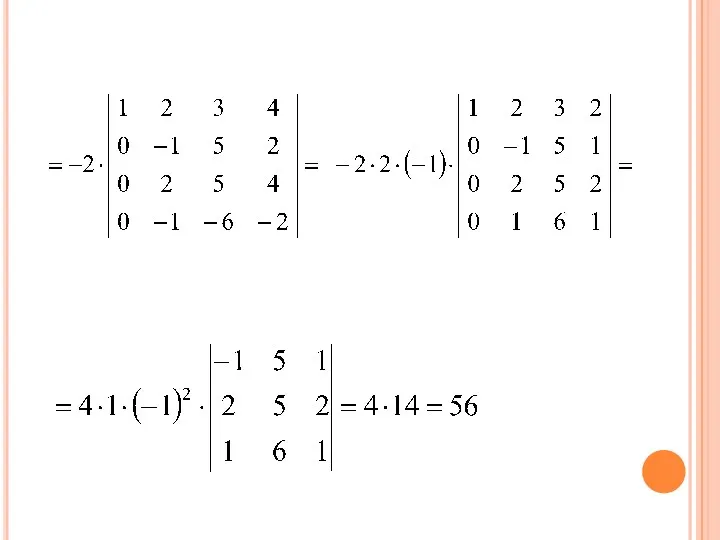










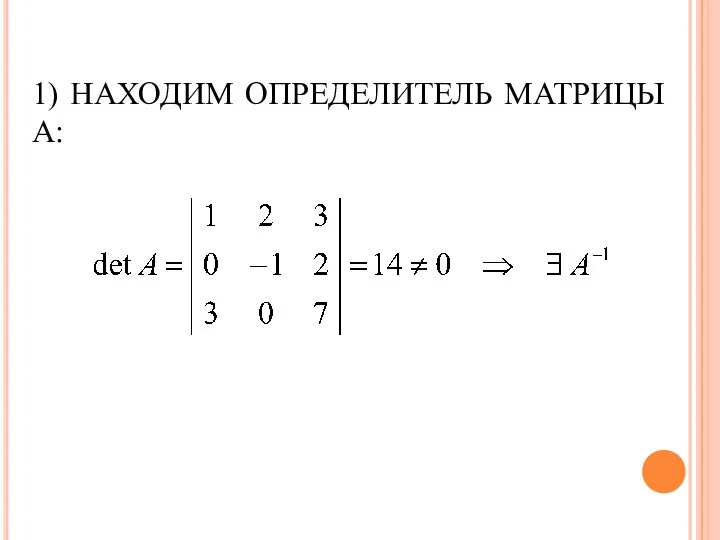
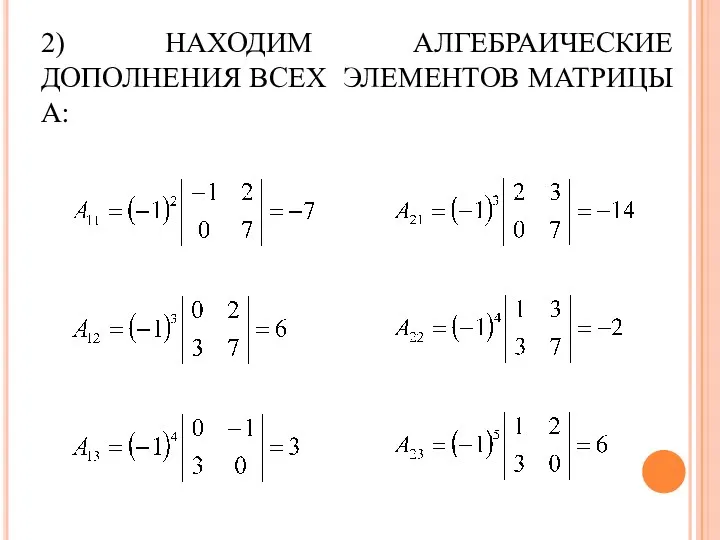
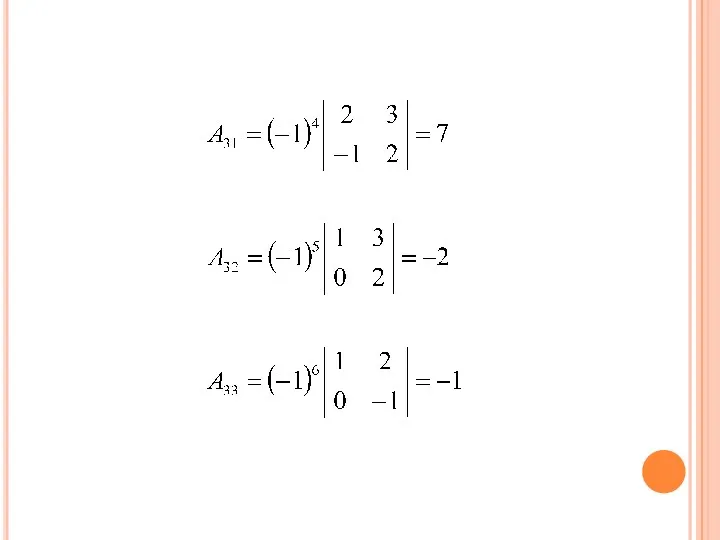




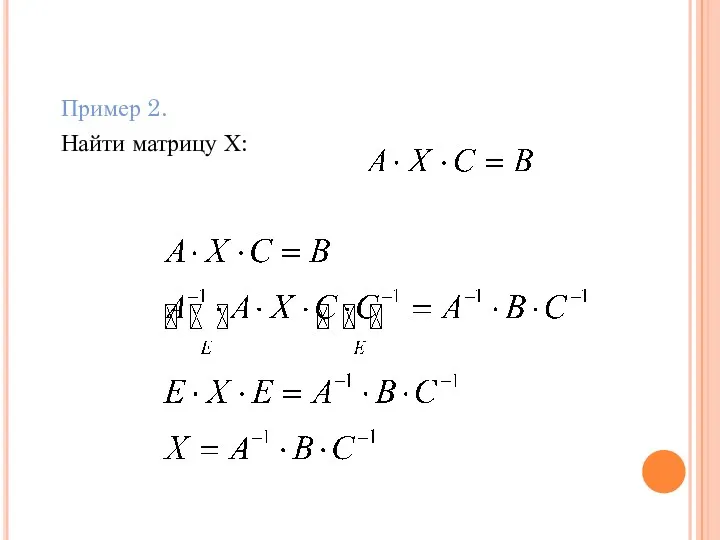
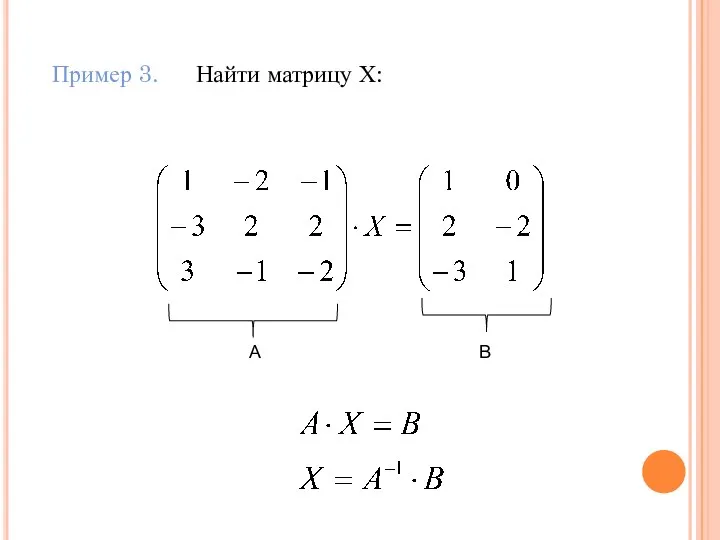
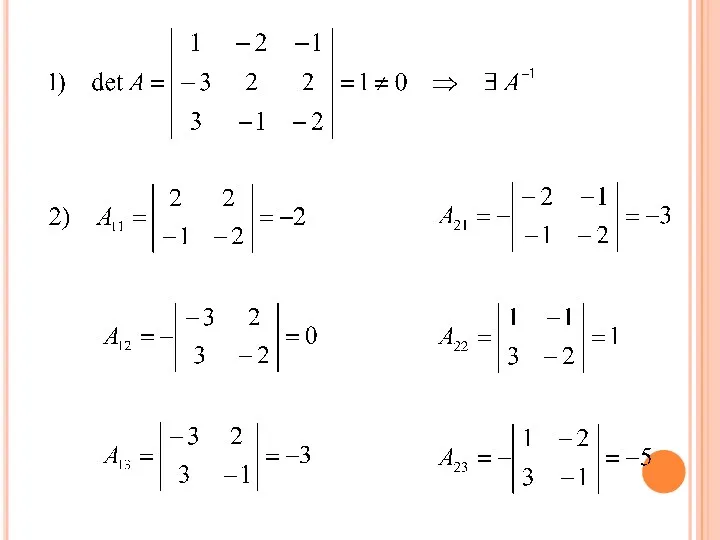
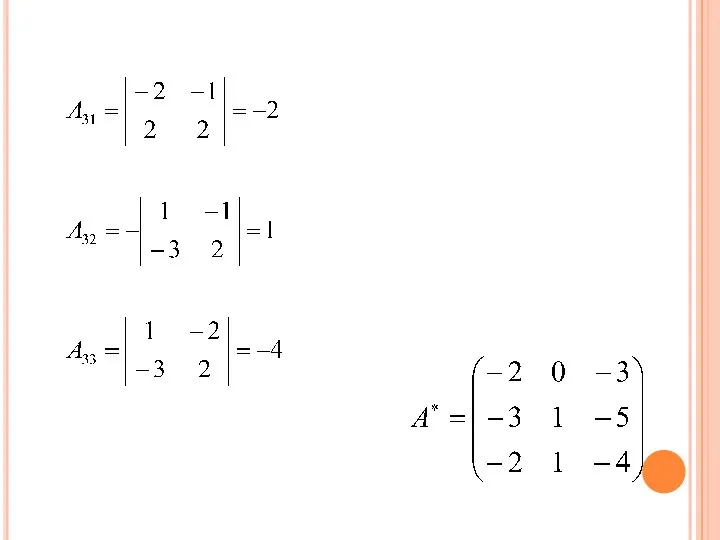
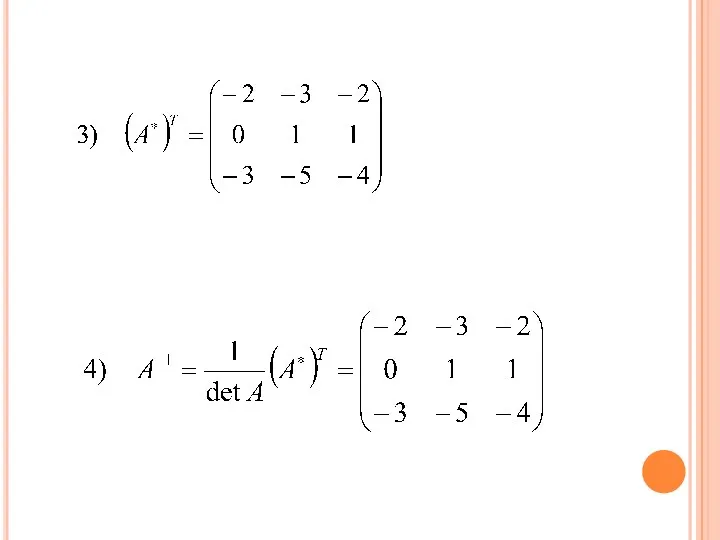
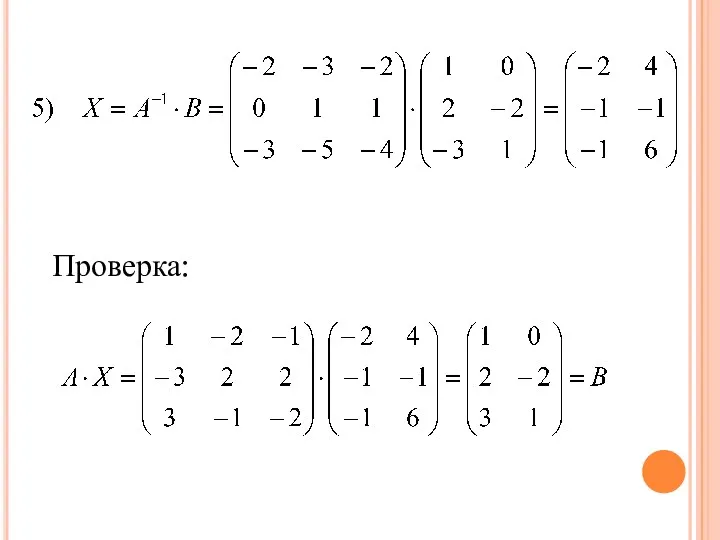


 Сложение и вычитание алгебраических дробей
Сложение и вычитание алгебраических дробей Разложение на простые множители
Разложение на простые множители Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении
Графики зависимости кинематических величин от времени при равномерном и равноускоренном движении Деление двузначного числа на однозначное.
Деление двузначного числа на однозначное. Применение производной к исследованию функции и построению графика функции
Применение производной к исследованию функции и построению графика функции Таблица умножения и деления на 3
Таблица умножения и деления на 3 Площадь многоугольников
Площадь многоугольников Именованные числа.
Именованные числа. Задачи раскраски графов. Вершинная раскраска
Задачи раскраски графов. Вершинная раскраска Сложение однозначных чисел с переходом через десяток, вида +2, +3
Сложение однозначных чисел с переходом через десяток, вида +2, +3 Параллелограмм. Свойства параллелограмма
Параллелограмм. Свойства параллелограмма Таблица сложения и вычитания в пределах 20 (КИМ 1 класс)
Таблица сложения и вычитания в пределах 20 (КИМ 1 класс) Математика. 1 класс. Урок 7. Порядок
Математика. 1 класс. Урок 7. Порядок Арифметическая прогрессия. Применение формул
Арифметическая прогрессия. Применение формул Урок математики в 3 классе по теме: Деление двузначного числа на однозначное
Урок математики в 3 классе по теме: Деление двузначного числа на однозначное Познавательно-игровой проект Применение игр и игровых упражнений с мячом в работе с детьми Диск
Познавательно-игровой проект Применение игр и игровых упражнений с мячом в работе с детьми Диск Электронные обучающие игры для средней группы: Продолжи ряд, Сколько всего?
Электронные обучающие игры для средней группы: Продолжи ряд, Сколько всего? Теорема синусов. Теорема косинусов
Теорема синусов. Теорема косинусов Урок математики в 1 классе по теме Число пять. Цифра 5.
Урок математики в 1 классе по теме Число пять. Цифра 5. Параллелограмм, трапеция, прямоугольник, квадрат, ромб. Обобщающий урок по геометрии для 8
Параллелограмм, трапеция, прямоугольник, квадрат, ромб. Обобщающий урок по геометрии для 8 Повторение, обобщение и систематизация знаний. Степени с рациональным показателем
Повторение, обобщение и систематизация знаний. Степени с рациональным показателем Формулы - помощники для расчета расстояния, определения скорости движения, времени в пути
Формулы - помощники для расчета расстояния, определения скорости движения, времени в пути Анализ временных рядов. (Тема 5)
Анализ временных рядов. (Тема 5) График линейной функции
График линейной функции Санның логарифмі. Негізгі логарифмдік тепе-теңдік. Логарифмнің қасиеттері
Санның логарифмі. Негізгі логарифмдік тепе-теңдік. Логарифмнің қасиеттері Пифагоров строй
Пифагоров строй Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Ryspekov’s Fibonacci sequence formula
Ryspekov’s Fibonacci sequence formula