Содержание
- 2. Примеры задач линейного программирования
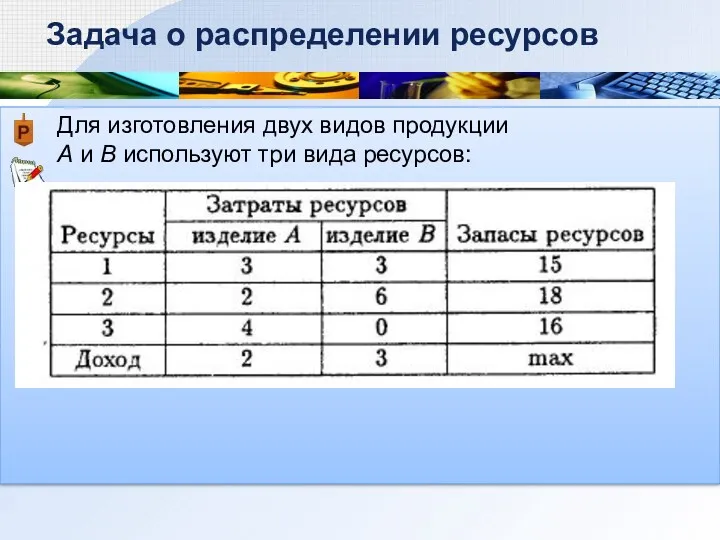
- 3. Для изготовления двух видов продукции А и В используют три вида ресурсов: Задача о распределении ресурсов
- 4. Изучение рынка сбыта показало, что объем выпуска изделий А не должен превышать объема изделий В более,
- 5. Решение Введем переменные Задача о распределении ресурсов х1 – число единиц продукции А, запланированных к производству
- 6. Решение Ограничения Задача о распределении ресурсов 1) Условие неотрицательности: 2) На запас сырья 1: 3) На
- 7. Математическая модель Задача о распределении ресурсов
- 8. В дневной рацион питания цыплят включают два продукта П1 и П2. Причем продукта П1 должно войти
- 9. Решение Введем переменные Задача о рационе (о диете) х1 – число единиц продукта П1, входящего в
- 10. Решение Ограничения Задача о рационе (о диете) 1) Условие неотрицательности: 2) Ограничение на максимальное содержание продукта
- 11. Математическая модель Задача о рационе (о диете)
- 12. Основные понятия
- 13. Термин линейное программирование линейное означает: ищется экстремальное значение (min или max) линейной целевой функции при линейных
- 14. Задача линейного программирования в общем виде (ЗЛП) – это задача о нахождении экстремума линейной функции на
- 15. Каноническая задача линейного программирования
- 16. Каноническая задача линейного программирования В канонической задаче ЛП (КЗЛП): 1) находится максимум целевой функции 2) все
- 17. В канонической задаче: 1) целевая функция → max 2) все ограничения - уравнения 3) все переменные
- 18. В канонической задаче: 1) целевая функция → max 2) все ограничения - уравнения 3) все переменные
- 19. В канонической задаче: 1) целевая функция → max 2) все ограничения - уравнения 3) все переменные
- 20. В канонической задаче: 1) целевая функция → max 2) все ограничения - уравнения 3) все переменные
- 21. Теоретическое обоснование Теорема Если целевая функция принимает максимальное значение в некоторой точке допустимого множества, то она
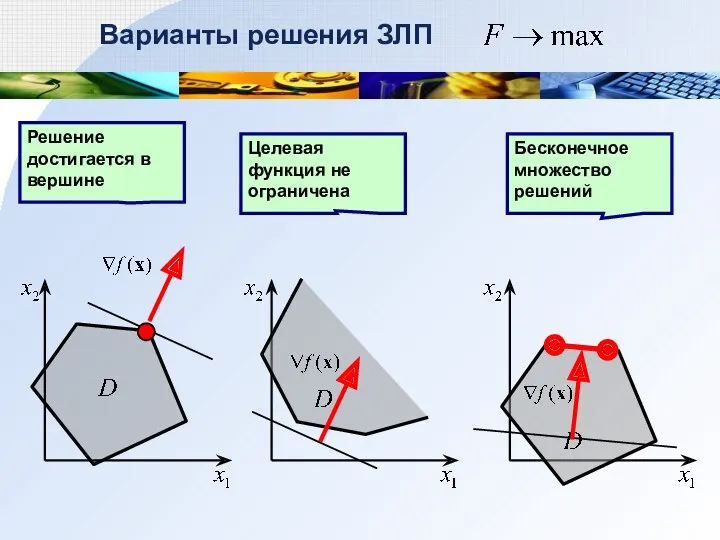
- 22. Решение достигается в вершине Целевая функция не ограничена Бесконечное множество решений Варианты решения ЗЛП
- 23. Графический метод решения
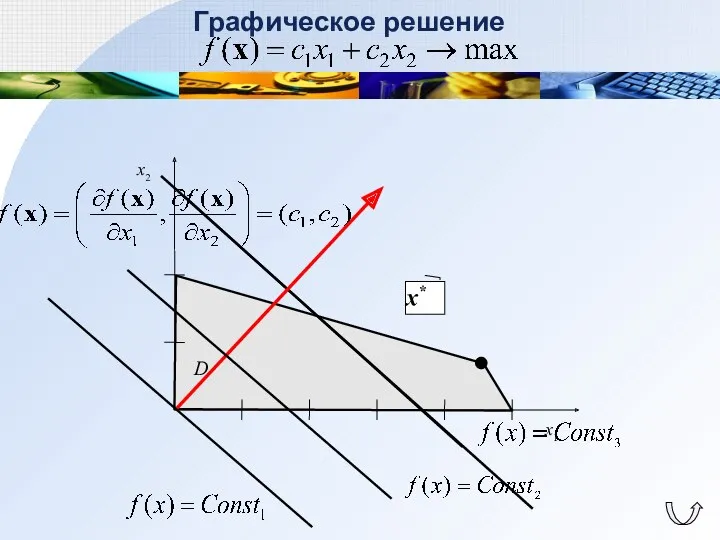
- 24. Графическое решение
- 25. Графическое решение Алгоритм решения Построить на плоскости допустимое множество Найти градиент целевой функции Найти оптимальный план
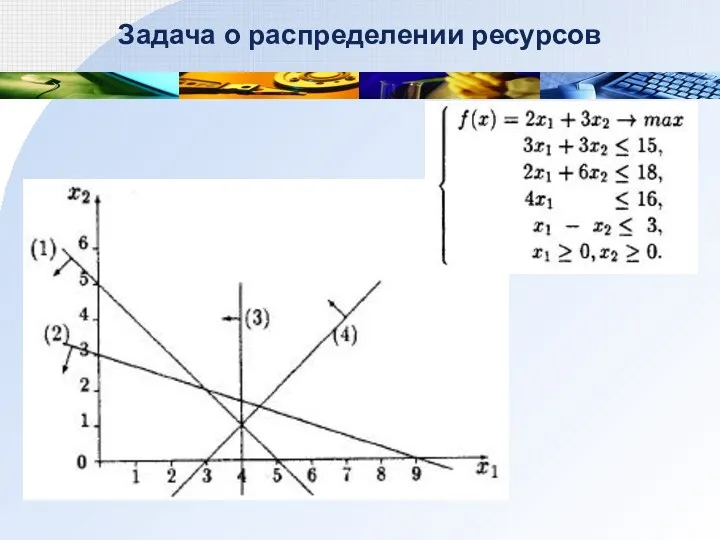
- 26. Задача о распределении ресурсов
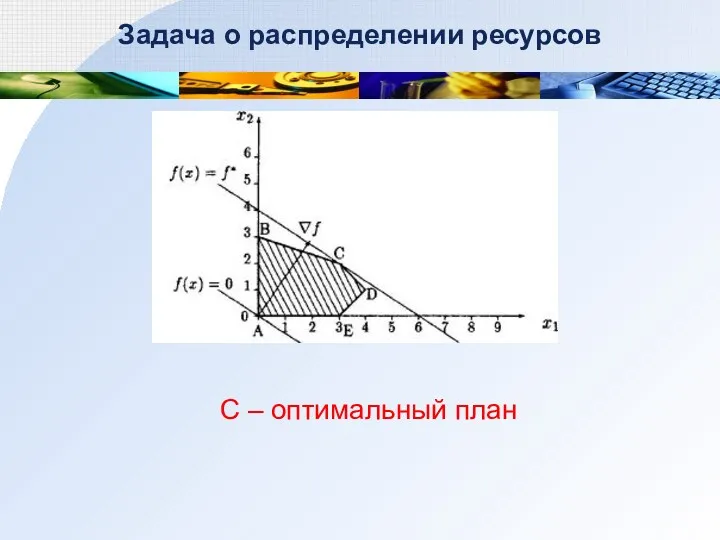
- 27. Задача о распределении ресурсов С – оптимальный план
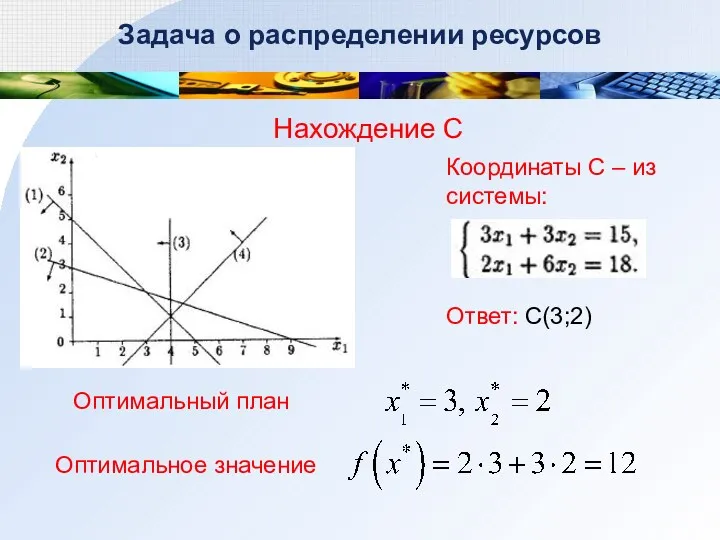
- 28. Задача о распределении ресурсов Нахождение С Координаты С – из системы: Ответ: С(3;2) Оптимальное значение Оптимальный
- 29. Симплекс-метод Симплекс ─ n-мерный многогранник
- 30. Основные теоретические сведения Система линейных уравнений ─ система с базисом, если в каждом уравнении есть базисная
- 31. Основные теоретические сведения Базисное решение ─ решение системы, соответствующее нулевым значениям свободных переменных. Опорный план ─
- 32. Основная теорема ЛП Если каноническая задача линейного программирования разрешима, то её оптимальный план содержится среди конечного
- 33. Пример Каноническая форма задачи: Она же ─ специальная!
- 34. Пример Опорный план: Значение целевой функции План не оптимальный! Увеличиваем (второе уравнение!)
- 35. Пример Проверка оптимальности Приведение задачи к специальному виду: Выражение целевой функции через свободные переменные План не
- 36. Пример Увеличиваем Опорный план: Соответствует базисным переменным Значение целевой функции
- 37. Пример Проверка оптимальности Приведение задачи к специальному виду: Выражение целевой функции через свободные переменные
- 38. Пример Табличная запись решения I этап 1. Самое маленькое отрицательное число в последней строке 2. Самое
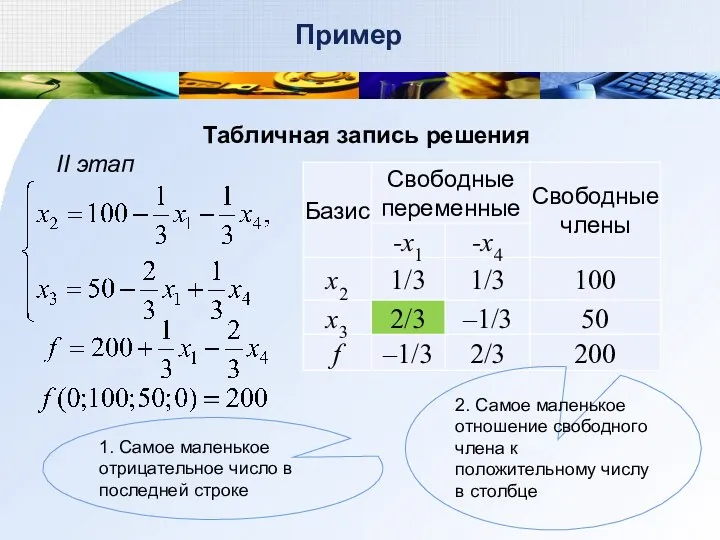
- 39. Пример Табличная запись решения II этап 1. Самое маленькое отрицательное число в последней строке 2. Самое
- 40. Пример Табличная запись решения III этап Нет отрицательных чисел!
- 41. Специальная задача ЛП Базисные переменные Свободные переменные
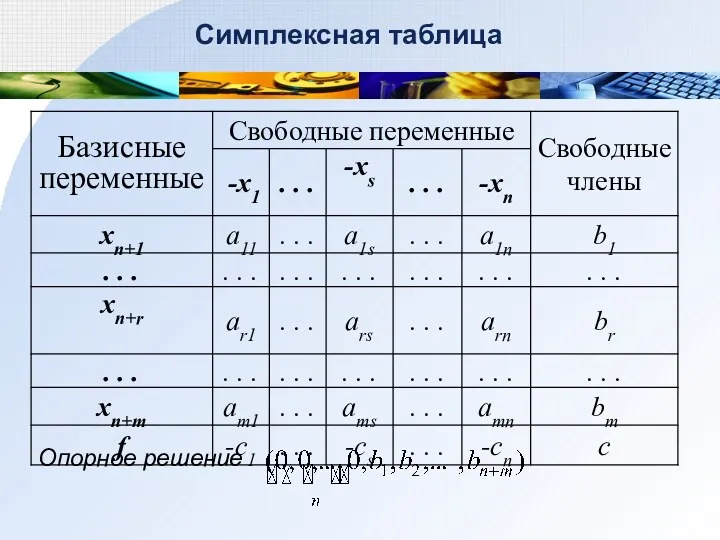
- 42. Симплексная таблица Опорное решение
- 43. Алгоритм симплекс-метода Подготовительный этап 1. Приведение к каноническому виду 2. Приведение к специальному виду 3. Составление
- 44. Алгоритм симплекс-метода Основной этап 1. Проверка оптимальности (все ли числа в последней строке неотрицательные) 2. Проверка
- 45. Алгоритм симплекс-метода Основной этап 3.Выбор ведущего столбца (по наименьшему отрицательному числу в последней строке) 4.Выбор ведущей
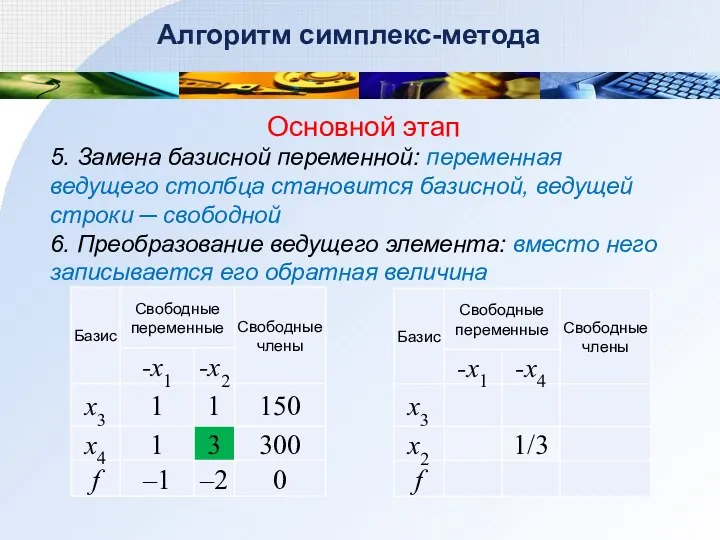
- 46. Алгоритм симплекс-метода Основной этап 5. Замена базисной переменной: переменная ведущего столбца становится базисной, ведущей строки ─
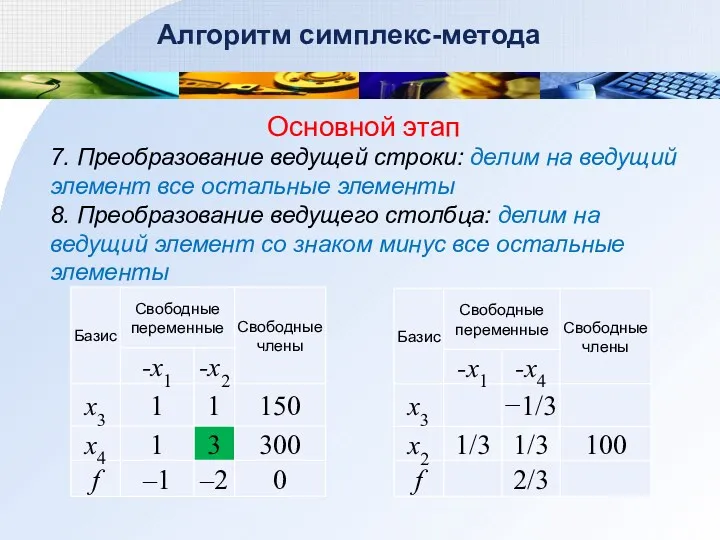
- 47. Алгоритм симплекс-метода Основной этап 7. Преобразование ведущей строки: делим на ведущий элемент все остальные элементы 8.
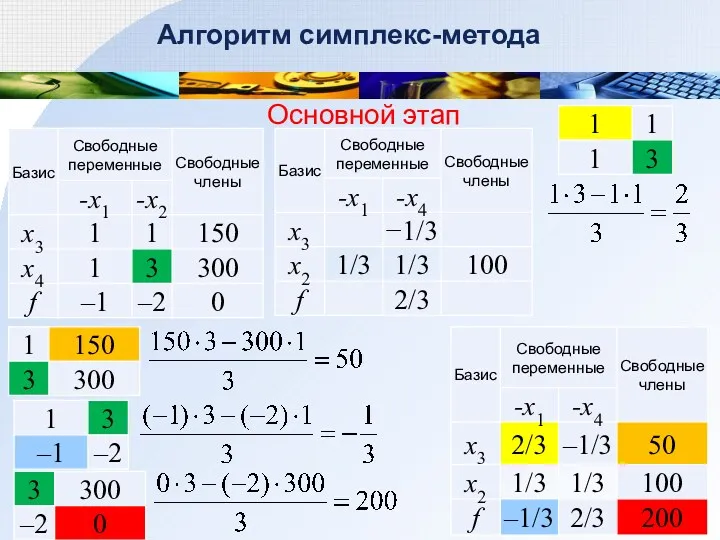
- 48. Алгоритм симплекс-метода Основной этап 8. Преобразование остальных элементов таблицы по правилу прямоугольника Новое значение
- 49. Алгоритм симплекс-метода Основной этап
- 50. Пример (распределении ресурсов) Каноническая форма задачи: Она же ─ специальная! Исходная модель
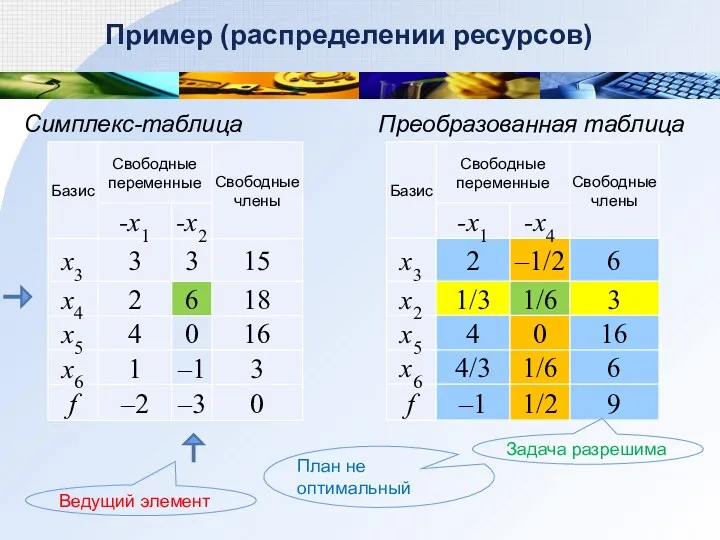
- 51. Пример (распределении ресурсов) Симплекс-таблица Задача разрешима План не оптимальный
- 52. Пример (распределении ресурсов) Симплекс-таблица Ведущий элемент Преобразованная таблица План не оптимальный Задача разрешима
- 54. Скачать презентацию







































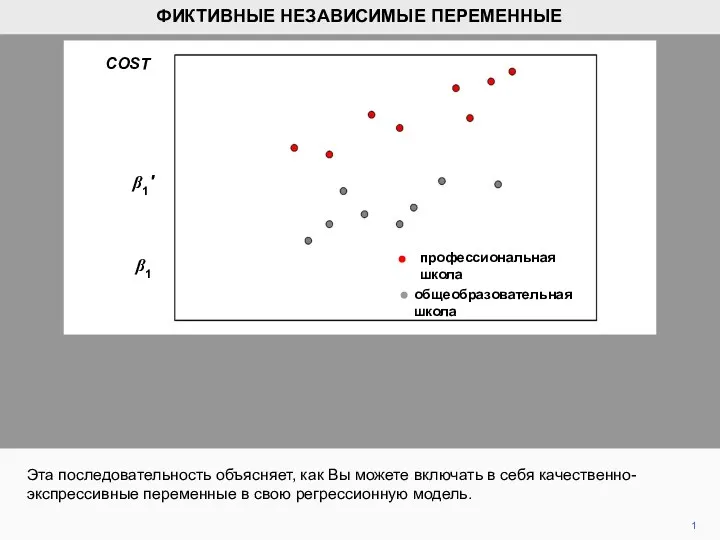 Фиктивные независимые переменные
Фиктивные независимые переменные Тренажёр для проверки таблицы умножения Смешарики Пояснительная записка
Тренажёр для проверки таблицы умножения Смешарики Пояснительная записка презентация Путешествие по математическим станциям
презентация Путешествие по математическим станциям Обчислення на основі нумерації (урок № 118)
Обчислення на основі нумерації (урок № 118) Статистикалық әдістер
Статистикалық әдістер Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Автокорреляция и ее последствия. Обнаружение автокорреляции и методы исправления
Автокорреляция и ее последствия. Обнаружение автокорреляции и методы исправления Функция y=k/x, её график и свойства
Функция y=k/x, её график и свойства Старинные меры длины и веса
Старинные меры длины и веса Конспект открытого урока по математике. тема: Масса. Килограмм.
Конспект открытого урока по математике. тема: Масса. Килограмм. Числа от 1-8. УМК Школа 2100
Числа от 1-8. УМК Школа 2100 Действия над векторами. Векторы на плоскости
Действия над векторами. Векторы на плоскости Основні поняття та аксіоми стереометрії
Основні поняття та аксіоми стереометрії Свойства прямоугольного треугольника. Задачи
Свойства прямоугольного треугольника. Задачи Оптимизация сетевых моделей
Оптимизация сетевых моделей Логарифмик тигезләмәләр
Логарифмик тигезләмәләр Компоненты сложения
Компоненты сложения Модуль действительного числа, уравнения
Модуль действительного числа, уравнения Понятие усеченной пирамиды
Понятие усеченной пирамиды Прямоугольный параллелепипед. Задания для устного счета. Упражнение 9
Прямоугольный параллелепипед. Задания для устного счета. Упражнение 9 Урок 31. Сравнение двузначных чисел
Урок 31. Сравнение двузначных чисел Значение синуса, косинуса и тангенса для углов 30°, 45°, 60°
Значение синуса, косинуса и тангенса для углов 30°, 45°, 60° Трапеция
Трапеция Определение декартовых координат. Координаты середины отрезка. Расстояние между точками
Определение декартовых координат. Координаты середины отрезка. Расстояние между точками Производная. Понятие о производной
Производная. Понятие о производной Признаки делимости на 10, на 5 и на 2. 6 класс
Признаки делимости на 10, на 5 и на 2. 6 класс Основания математики. Элементы теории графов
Основания математики. Элементы теории графов Математика. 1 класс. Урок 79. Сравнение. Сложение и вычитание величин - Презентация
Математика. 1 класс. Урок 79. Сравнение. Сложение и вычитание величин - Презентация