Содержание
- 2. Пример.
- 3. Оператор называется линейным, если для любых векторов x и y пространства и любого числа выполняются соотношения:
- 4. Пример. Будет ли указанный оператор линейным? Пусть Тогда Значит, оператор A не является линейным.
- 5. Пример. Будет ли указанный оператор линейным? Пусть Тогда Свойство аддитивности выполняется.
- 6. Свойство однородности выполняется. Значит, оператор A является линейным. В дальнейшем будем рассматривать линейные операторы
- 7. Матрица оператора Пусть — базис пространства . Тогда для любого вектора Если — линейный оператор, то
- 8. Так как то Поэтому (1)
- 9. С другой стороны, т.к. , то Из (1) и (2) получаем (2)
- 10. Матрица называется матрицей линейного оператора в базисе . Любой линейный оператор можно записать с помощью матричного
- 11. Замечание. Для того, чтобы найти матрицу линейного оператора, достаточно найти образы базисных векторов. Пример. Найти матрицу
- 12. Связь между матрицами оператора в разных базисах Теорема. Матрицы A и линейного оператора в разных базисах
- 13. Пример. Матрица линейного оператора в базисе имеет вид Найти матрицу этого оператора в базисе Решение. Матрица
- 15. Скачать презентацию
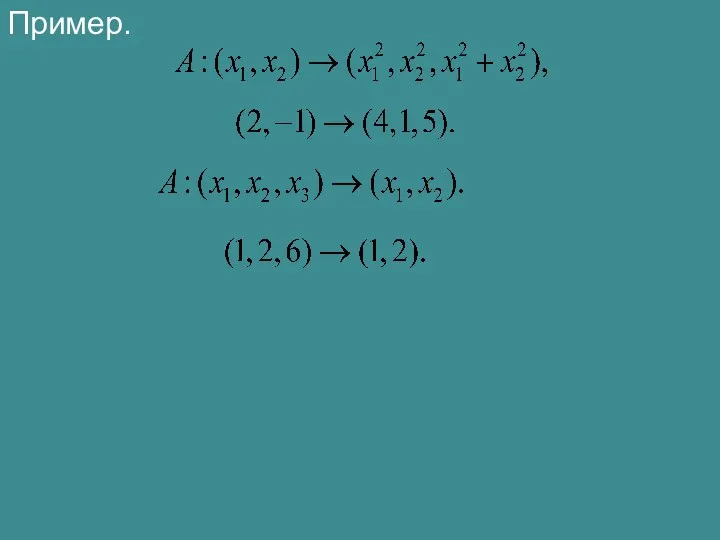





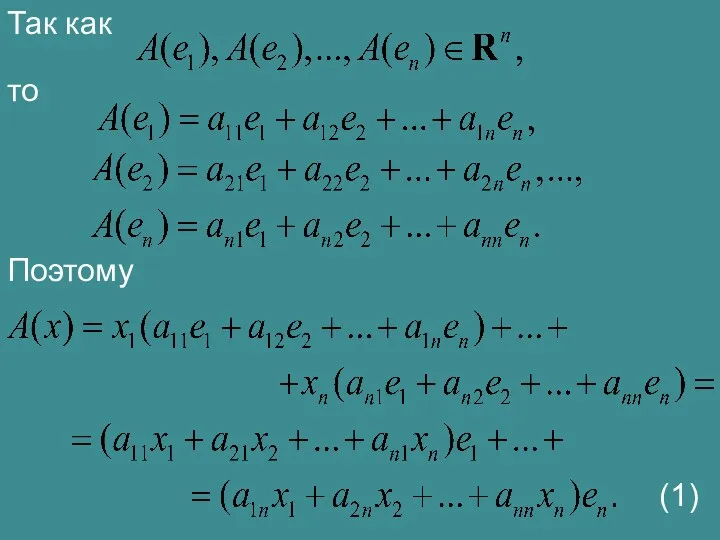





 Разложение вектора по трем некомпланарным
Разложение вектора по трем некомпланарным Устный счёт
Устный счёт Производная сложной функции
Производная сложной функции Приращение функции
Приращение функции Сравнение десятичных дробей
Сравнение десятичных дробей Интегрированный урок математики и музыки по теме Решение задач на части.
Интегрированный урок математики и музыки по теме Решение задач на части. Применение производной в химии и биологии
Применение производной в химии и биологии Число и цифра 8.
Число и цифра 8. Функция. Область определения и множество значений функции
Функция. Область определения и множество значений функции Геометрические фигуры. Отрезок. Длина отрезка
Геометрические фигуры. Отрезок. Длина отрезка Тең бүйірлі үшбұрыш және оның қасиеттері
Тең бүйірлі үшбұрыш және оның қасиеттері Письменное деление трехзначного числа на однозначное вида 748:2, 856:4
Письменное деление трехзначного числа на однозначное вида 748:2, 856:4 Квадрат. Периметр квадрата
Квадрат. Периметр квадрата Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Разложение на множители суммы и разности кубов
Разложение на множители суммы и разности кубов Самостійна робота. Математика
Самостійна робота. Математика Дистанционный урок по математике 10 марта
Дистанционный урок по математике 10 марта Объем куба, прямоугольного параллелепипеда и призмы
Объем куба, прямоугольного параллелепипеда и призмы Название чисел в записи действий. Закрепление.
Название чисел в записи действий. Закрепление. Действия над обыкновенными дробями
Действия над обыкновенными дробями Диаграммы. Построение диаграммы
Диаграммы. Построение диаграммы Divide et impera. Metodei şi aplicaţii
Divide et impera. Metodei şi aplicaţii Линейная функция и ее график
Линейная функция и ее график Использование определенного интеграла при решении экономических задач
Использование определенного интеграла при решении экономических задач Презентация Вычитание вида 35-7 по математике УМК Школа России 2 класс
Презентация Вычитание вида 35-7 по математике УМК Школа России 2 класс Конспект урока математики тема Обобщение знаний о геометрических фигурах 2класс
Конспект урока математики тема Обобщение знаний о геометрических фигурах 2класс Среднее арифметическое
Среднее арифметическое Системы счисления. Основные понятия
Системы счисления. Основные понятия