Содержание
- 2. Визначники другого і третього порядку. Властивості визначників. Матриці та дії з ними. Ранг матриці. Обернена матриця.
- 3. - визначник другого порядку - визначник третього порядку Розклад визначника за рядком або стовпцем: Визначники
- 4. Визначник не зміниться, якщо його рядки замінити відповідними стовпцями. Якщо переставити місцями два рядки (стовпці), то
- 5. Правило трикутника або правило Сарруса.
- 6. Мінором елемента визначника 3-го порядку називається визначник другого порядку, одержаний після викреслювання і-го рядка і j-го
- 7. Матриці Матрицею розміру m × n називається прямокутна таблиця з m × n чисел - елементи
- 8. Матриця називається нульовою, якщо всі її елементи дорівнюють 0. Дії над матрицями Сумою (різницею) двох матриця
- 9. А+В=В+А; А+О=А; О+А=А. Матриці А і В називаються протилежними, якщо їх сума А+В=О є нуль-матриця. Добутком
- 10. Операція множення матриці на число має розподільну властивість. λ ( А + В ) = λА
- 11. де A · 0 = 0 A · E = A A · B = B
- 12. Обернена матриця Оберненою для заданої квадратної матриці А називається така матриця , добуток на яку матриці
- 13. ІІІ. Знаходимо алгебраїчні доповнення кожного елемента транспонованої матриці А´ і записуємо їх у вигляді матриці (приєднана)
- 14. Розв’язування систем лінійних рівнянь різними способами (1) – система m лінійних рівнянь з n - невідомим
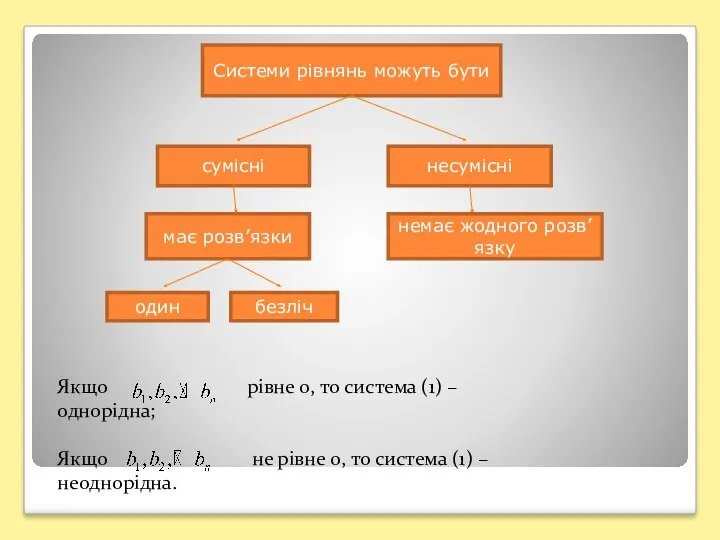
- 15. Системи рівнянь можуть бути сумісні несумісні має розв’язки немає жодного розв’язку один безліч Якщо рівне 0,
- 16. Основна матриця системи рівнянь Розширена матриця системи рівнянь (2) (3) Способи розв’язування систем рівнянь Системи рівнянь
- 17. Крамер народився в сім'ї лікаря. З раннього віку показав великі здібності до математики. У 18 років
- 18. Спосіб Крамера (для випадку m=n)
- 19. Гаусс Карл Фрідріх Характерними рисами досліджень Гаусса є надзвичайна їх різнобічність і органічний зв'язок у них
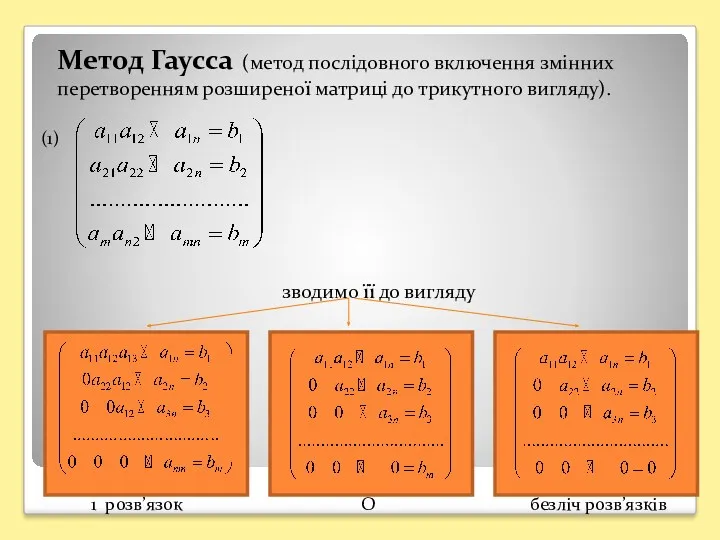
- 20. Метод Гаусса (метод послідовного включення змінних перетворенням розширеної матриці до трикутного вигляду). (1) зводимо її до
- 21. Нехай дано систему (1) (для випадку m=n) А – основна матриця, Х – матриця стовпець із
- 22. Перепишемо систему (1) у вигляді матричного рівняння А · Х = В. Його розв’язок - називається
- 24. Скачать презентацию



















 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Эконометрика. Обобщенный метод наименьших квадратов
Эконометрика. Обобщенный метод наименьших квадратов Треугольник. Четырехугольник. Окружность. Путешествие в геометрию
Треугольник. Четырехугольник. Окружность. Путешествие в геометрию Применение производной и первообразной показательной и логарифмической функции
Применение производной и первообразной показательной и логарифмической функции Неравенства
Неравенства Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке Величины 1 класс
Величины 1 класс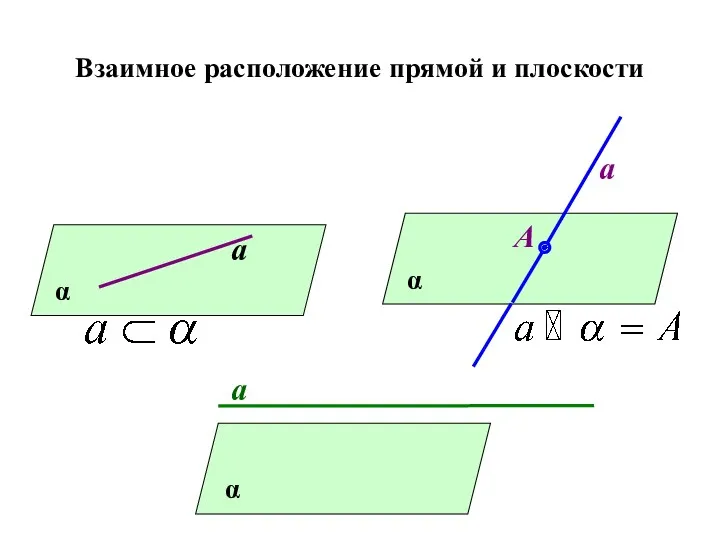 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости 20231001_mnogougolniki
20231001_mnogougolniki Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени
Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Как правильно писать цифры
Как правильно писать цифры Элементы теории вероятностей
Элементы теории вероятностей Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Тренировочная работа № 3
Тренировочная работа № 3 Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Представление натуральных чисел на координатном луче
Представление натуральных чисел на координатном луче Скорость, время, расстояние. Математика, 4класс.
Скорость, время, расстояние. Математика, 4класс. ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов
ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Геометрические фигуры
Геометрические фигуры Математика. 1 класс. Урок 4. Признаки предметов
Математика. 1 класс. Урок 4. Признаки предметов Задача по финансовой математике
Задача по финансовой математике Правильный додекаэдр
Правильный додекаэдр Геометрические фигуры (презентация для подготовки)
Геометрические фигуры (презентация для подготовки) Вклад математиков в победу Великой Отечественной Войне
Вклад математиков в победу Великой Отечественной Войне Конспект урока математики (+ презентация). 4 класс
Конспект урока математики (+ презентация). 4 класс