Содержание
- 2. Аристотель (384— 322 гг. до н. э.) Джордж Буль (1815 – 1864)
- 3. Основные понятия алгебры логики АЛГЕБРА ЛОГИКИ – математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют
- 4. Логическая (двоичная, булева) переменная — это такая переменная, которая может принимать одно из двух значений: истина
- 5. Логическая константа — это такая постоянная величина, значением которой может быть истинно или ложно (да или
- 6. Логическая функция — это такая функция, которая может принимать одно из двух значений: истинно или ложно
- 7. Логическая (булева, переключательная) функция f, зависящая от n переменных x1,x2, … xn, принимает значения только 0
- 8. Логическая функция может быть одного (n = 1) или нескольких (n > 1) аргументов. Значение логической
- 9. Булеву функцию от n переменных можно рассматривать как n-местную алгебраическую операцию на множестве B={0,1}. При этом
- 10. Способы задания булевых функций словесным описанием; таблицей истинности; логическим выражением. Используется в случае сравнительно несложной логической
- 11. Таблица истинности является универсальным средством задания логической функции. Включает все наборы для заданного количества переменных, определяющих
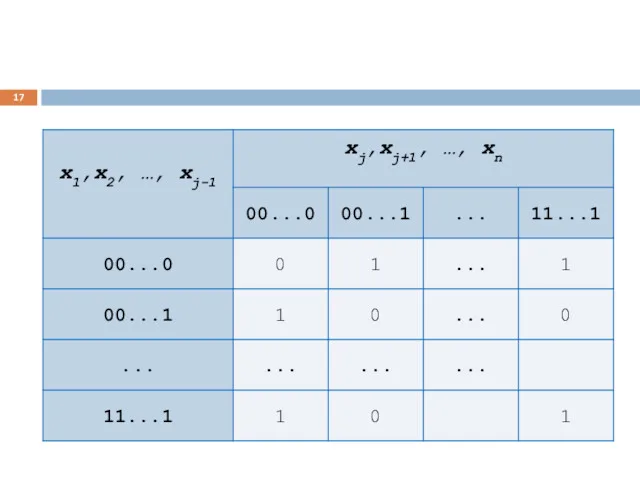
- 12. Табличный способ предполагает, что в левой части будут записаны все возможные двоичные наборы длины n (комбинации
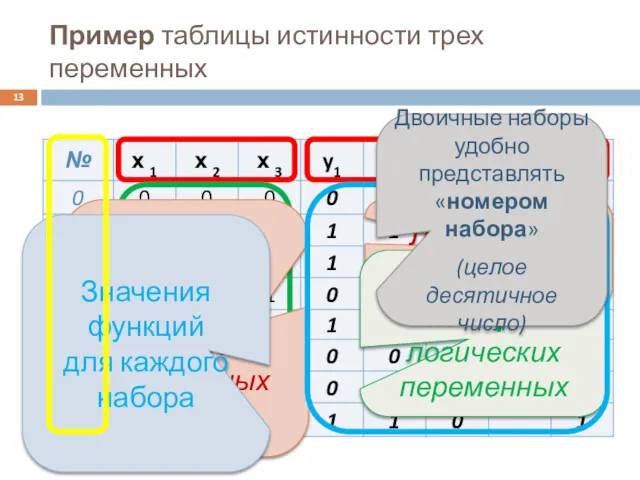
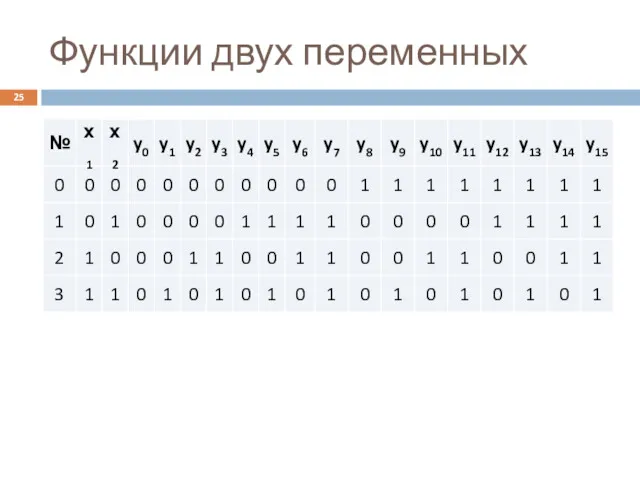
- 13. Пример таблицы истинности трех переменных Логические переменные Двоичные наборы логических переменных Логические функции, заданные на одинаковых
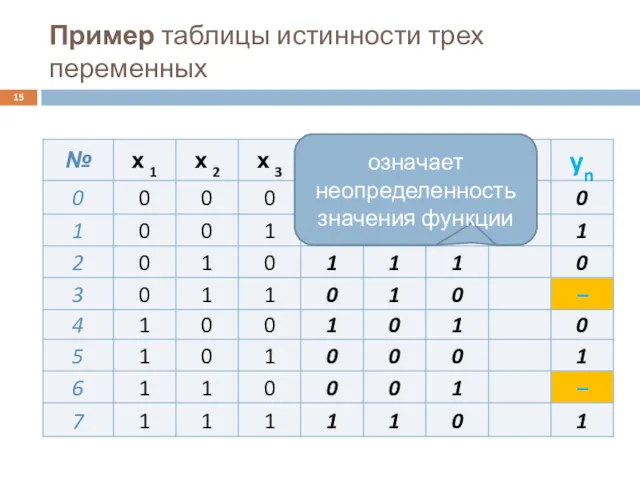
- 14. Логическая функция называется «полностью определенной», если для нее заданы значения по всем возможным наборам. Функция называется
- 15. Пример таблицы истинности трех переменных
- 16. Булевы функции от большого числа переменных таблицей истинности задавать сложно (громоздко). Например, Для функции от 8
- 18. При аналитическом способе задания булевой функции используется формула, т.е. аналитическое выражение, построенное из операций булевой алгебры.
- 19. Логическое выражение – комбинация логических переменных и констант, связанных элементарными базовыми логическими функциями (или логическими операциями),
- 20. Набор элементарных логических операций, с помощью которых можно задать любую, сколь угодно сложную логическую функцию, называется
- 21. В качестве элементарных логических функций функционально полных систем этих функций используются функции одной или двух логических
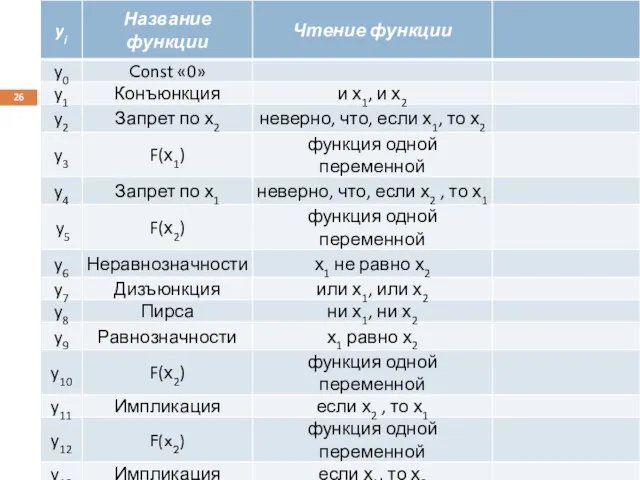
- 22. Функции одной переменной y0 = 0 – константа; y1 равна значению переменной x; y2 равна значению,
- 23. Функции одной переменной
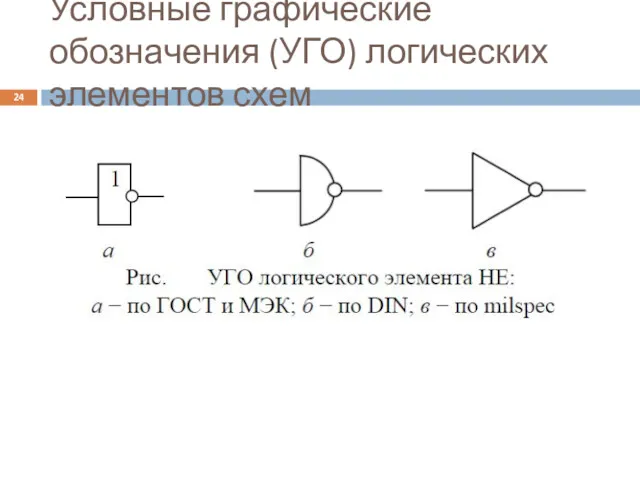
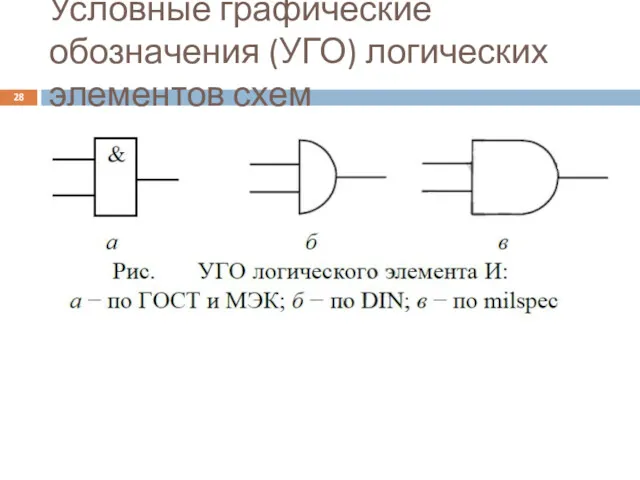
- 24. Условные графические обозначения (УГО) логических элементов схем
- 25. Функции двух переменных
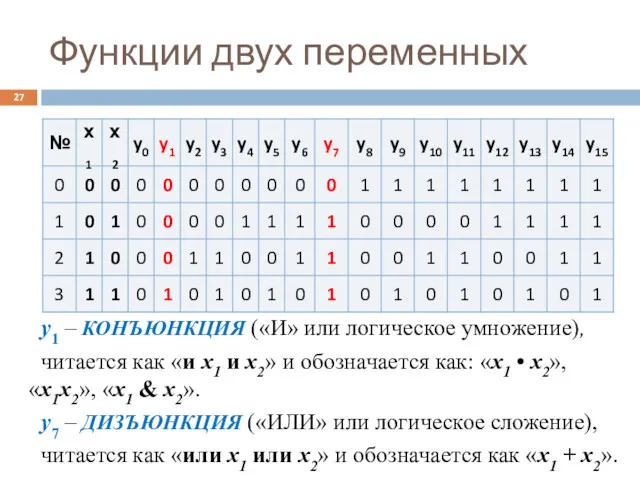
- 27. Функции двух переменных y1 – КОНЪЮНКЦИЯ («И» или логическое умножение), читается как «и х1 и x2»
- 28. Условные графические обозначения (УГО) логических элементов схем
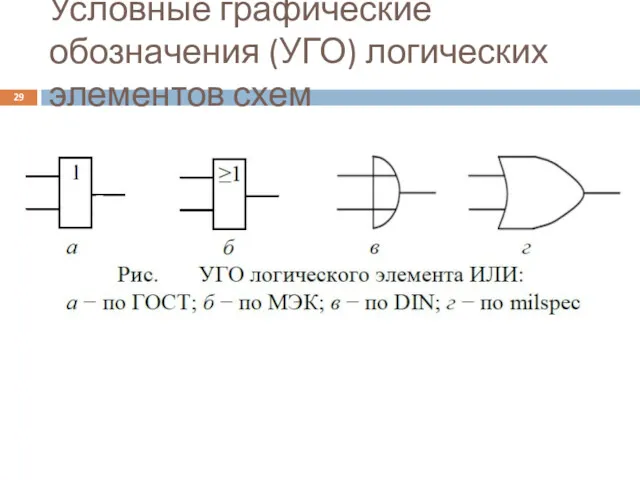
- 29. Условные графические обозначения (УГО) логических элементов схем
- 30. Наиболее распространенной в алгебре логики является ФПСЛФ, которая в качестве базовых логических функций использует функцию одной
- 31. Из всех функций от двух переменных можно выделить еще так называемые «Стрелка Пирса» и «Штрих Шеффера».
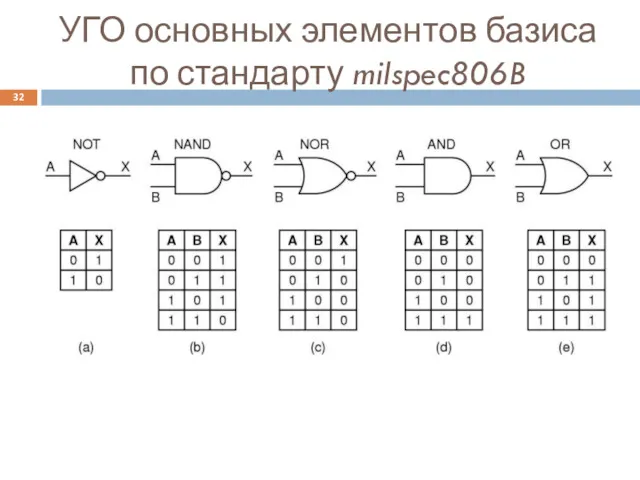
- 32. УГО основных элементов базиса по стандарту milspec806B
- 33. Булева алгебра В алгебре логики выделяют целый раздел «алгебра Буля», посвященный булевому базису. В алгебре Буля
- 34. Джордж Буль – создатель алгебры логики
- 35. Булева алгебра При оценке значения логического выражения необходимо решить его для конкретного набора переменных. В алгебре
- 36. Законы булевой алгебры: Закон справедлив и для конъюнкции и для дизъюнкции. х1 + х2 + х3
- 37. Законы булевой алгебры: Закон справедлив и для конъюнкции и для дизъюнкции. х1 + х2 + х3
- 38. Законы булевой алгебры: х1 + х2 х3 = (х1 + х2) ( х1 + х3) дизъюнкция
- 39. Законы булевой алгебры: отрицание суммы равно произведению отрицаний; отрицание произведения равно сумме отрицаний. Правило де Моргана
- 40. Законы булевой алгебры: Операции с одинаковыми операндами. Правило повторения (идемпотентности): х1 + х1 + х1 +
- 41. Законы булевой алгебры: Доказательство: х1 + (х1•х2) = (х1 •1) + (х1•х2) = х1 •(1 +
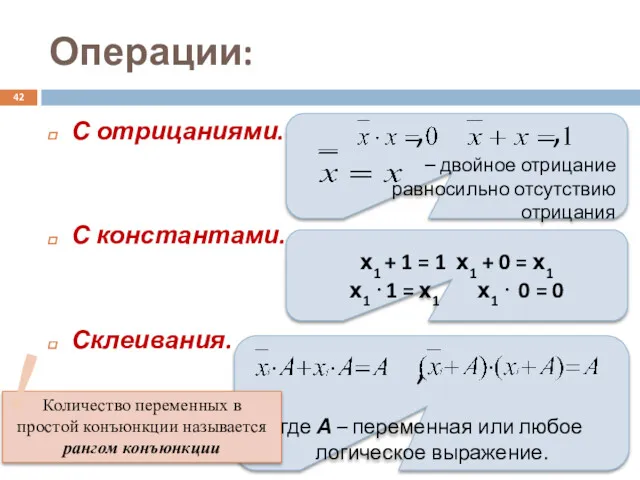
- 42. Операции: С отрицаниями. С константами. Склеивания. , , – двойное отрицание равносильно отсутствию отрицания х1 +
- 44. Скачать презентацию






























 Радианная мера угла
Радианная мера угла Площадь фигуры
Площадь фигуры Линейные уравнения. 7 класс
Линейные уравнения. 7 класс Практическое применение теорем геометрии в жизни
Практическое применение теорем геометрии в жизни Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Единицы измерения площадей
Единицы измерения площадей Фиктивные переменные в регрессионных моделях
Фиктивные переменные в регрессионных моделях Смежные углы
Смежные углы Однополостный гиперболоид
Однополостный гиперболоид презентация к коспекту занятия Измерение длины по Л.Г. Петерсону Диск Диск Диск
презентация к коспекту занятия Измерение длины по Л.Г. Петерсону Диск Диск Диск Выражения и их преобразования
Выражения и их преобразования Формула стоимости
Формула стоимости Урок математики (3 класс)
Урок математики (3 класс) Разложение многочленов на множители
Разложение многочленов на множители Построение смешанного сопряжения двух окружностей
Построение смешанного сопряжения двух окружностей Векторы в пространстве
Векторы в пространстве тренажёр для отработки знания таблицы умножения
тренажёр для отработки знания таблицы умножения Математический КВН для 3 класса
Математический КВН для 3 класса Абсолютные, относительные и средние величины в статистике. Показатели вариации в статистике
Абсолютные, относительные и средние величины в статистике. Показатели вариации в статистике Нумерация чисел в пределах 10. (1 класс)
Нумерация чисел в пределах 10. (1 класс) Роль математики в медицине
Роль математики в медицине Приемы устных вычислений в пределах 1000. 3 класс
Приемы устных вычислений в пределах 1000. 3 класс Прямоугольник. Квадрат
Прямоугольник. Квадрат Сложение однозначных чисел с переходом через десяток
Сложение однозначных чисел с переходом через десяток Шуточные математические задачи
Шуточные математические задачи Правильные и неправильные дроби
Правильные и неправильные дроби Общие методы решения уравнений
Общие методы решения уравнений