Содержание
- 2. Математическую модель САУ используют для изучения работы систем автоматического регулирования при установившемся режиме работы, а также
- 3. Дифференциальное уравнение САУ ai, bi - постоянные коэффициенты, у – управляемая (выходная) величина, х – входная
- 4. Дифференциальное уравнение САУ В операторной форме это уравнение: D(p) – оператор левой части М(р) – оператор
- 5. Дифференциальное уравнение САУ Часто используют понятие передаточной функции, выражение которой получают: Передаточная функция – это отношение
- 6. Преобразование Лапласа Для решения дифференциального уравнения системы используют метод анализа, основанный на преобразованиях Лапласа. Тема 6.
- 7. Преобразование Лапласа Тема 6. «Математические модели САУ»
- 8. Преобразование Лапласа Применив преобразование Лапласа к дифференциальному уравнению, получим связь изображений входной и выходной функций: Тема
- 9. Амплитудно-фазовая частотная (АФЧ) характеристика системы Если в выражение передаточной функции подставить вместо оператора р мнимую переменную
- 10. Линейные системы Для линейных систем передаточная функция исчерпывающе характеризует поведение системы при любых возмущениях, так как
- 11. ПРИМЕР: Пусть передаточная функция имеет вид: Тема 6. «Математические модели САУ» Поскольку изображение функции изменения выходного
- 12. Замечание Тема 6. «Математические модели САУ» Для получения математической модели автоматической системы необходимо все реальные элементы
- 13. Типовые динамические звенья и способы их соединения. Тема 6. «Математические модели САУ» Типовое динамическое звено –
- 14. БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» Звенья у которых при скачкообразном изменении входного сигнала, выходной
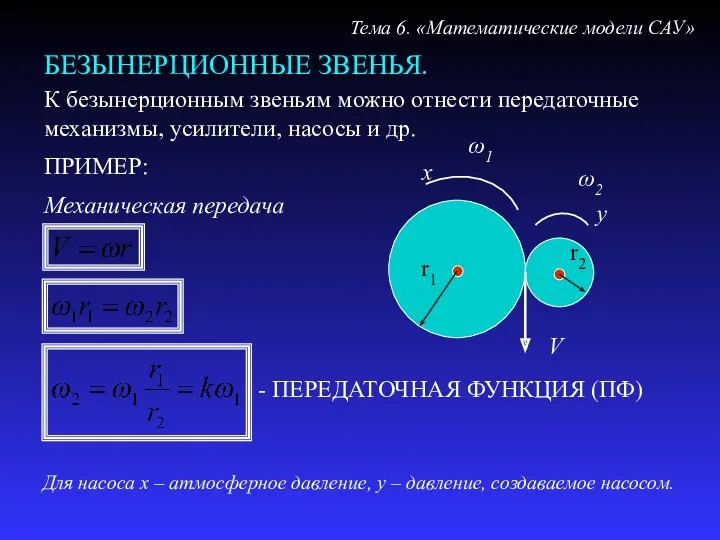
- 15. БЕЗЫНЕРЦИОННЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» К безынерционным звеньям можно отнести передаточные механизмы, усилители, насосы
- 16. ИНЕРЦИОННЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» при скачкообразном изменении входного сигнала, выходной сигнал стремиться к
- 17. ИНЕРЦИОННЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» К инерционным звеньям можно отнести баки с жидкостью, электродвигатели
- 18. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» при скачкообразном изменении входного сигнала, выходной сигнал колеблется относительного
- 19. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» К колебательным звеньям можно отнести объекты, имеющие подпружиненную массу,
- 20. ДИФФЕРЕНЦИРУЮЩИЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» Выходной сигнал пропорционален скорости изменения входного сигнала. ДИФФУР (ДУ):
- 21. ИНТЕГРИРУЮЩИЕ ЗВЕНЬЯ. Тема 6. «Математические модели САУ» звено, в котором выходная величина пропорциональна интегралу по времени
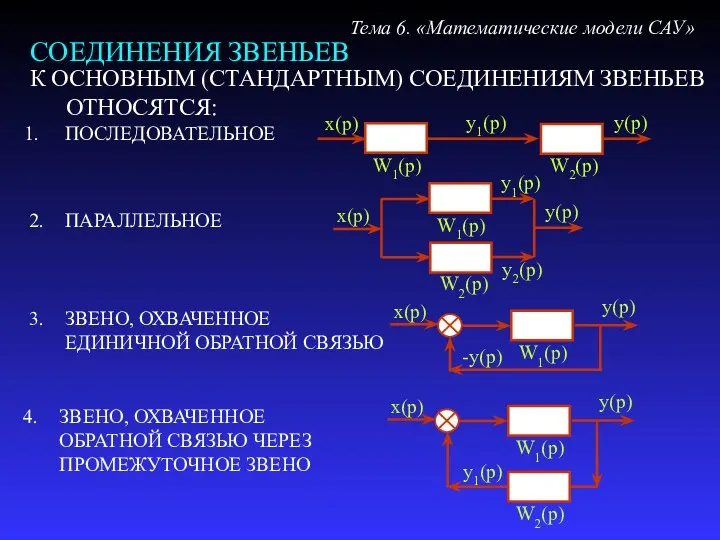
- 22. СОЕДИНЕНИЯ ЗВЕНЬЕВ Тема 6. «Математические модели САУ» К ОСНОВНЫМ (СТАНДАРТНЫМ) СОЕДИНЕНИЯМ ЗВЕНЬЕВ ОТНОСЯТСЯ: 4. ЗВЕНО, ОХВАЧЕННОЕ
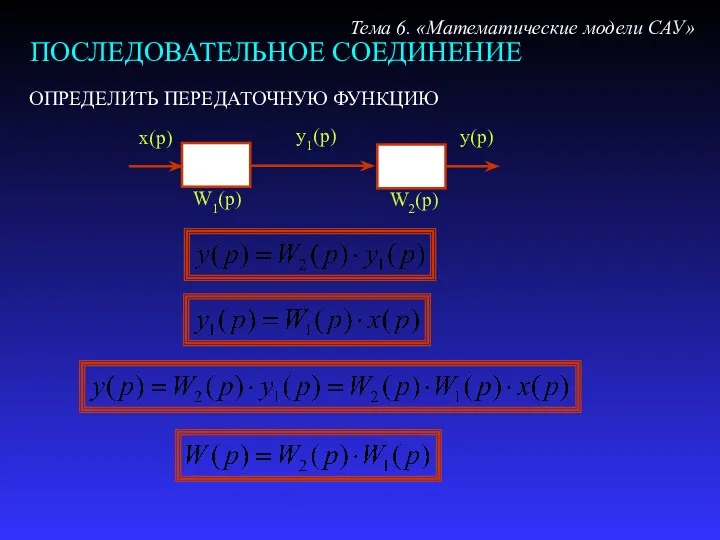
- 23. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ Тема 6. «Математические модели САУ» ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
- 24. ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ Тема 6. «Математические модели САУ» ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
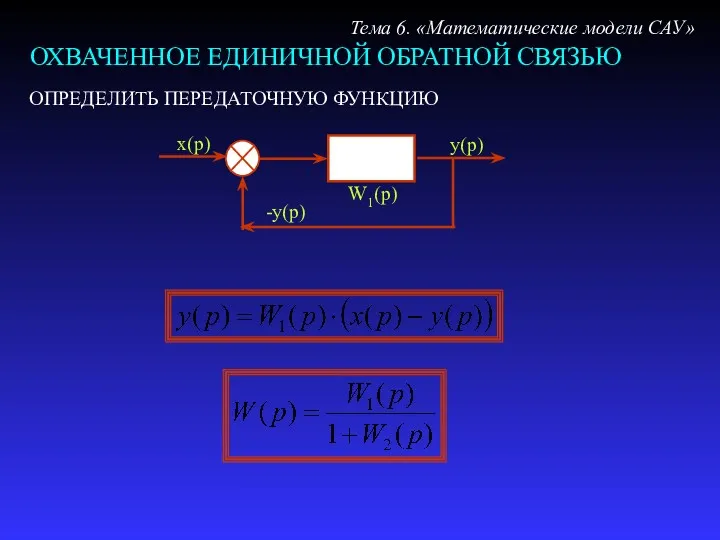
- 25. ОХВАЧЕННОЕ ЕДИНИЧНОЙ ОБРАТНОЙ СВЯЗЬЮ Тема 6. «Математические модели САУ» ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
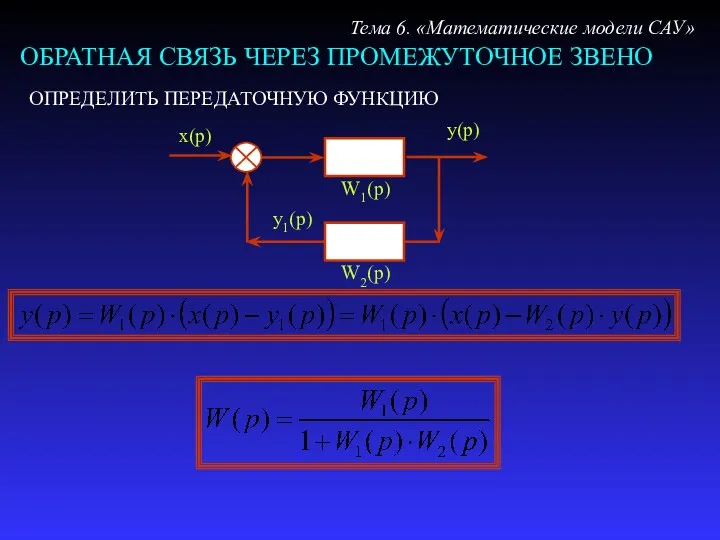
- 26. ОБРАТНАЯ СВЯЗЬ ЧЕРЕЗ ПРОМЕЖУТОЧНОЕ ЗВЕНО Тема 6. «Математические модели САУ» ОПРЕДЕЛИТЬ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ
- 27. ТЕХНОЛОГИЯ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ УПРАВЛЕНИЯ Тема 6. «Математические модели САУ» Для получения математической модели
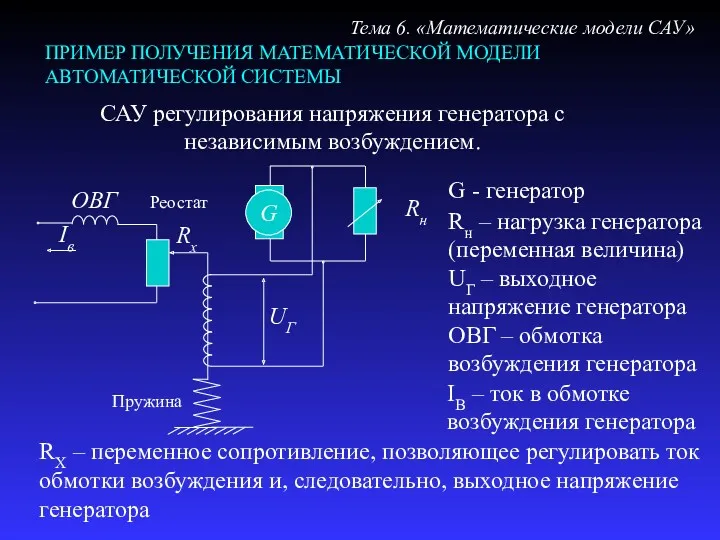
- 28. ПРИМЕР ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ АВТОМАТИЧЕСКОЙ СИСТЕМЫ Тема 6. «Математические модели САУ» САУ регулирования напряжения генератора с
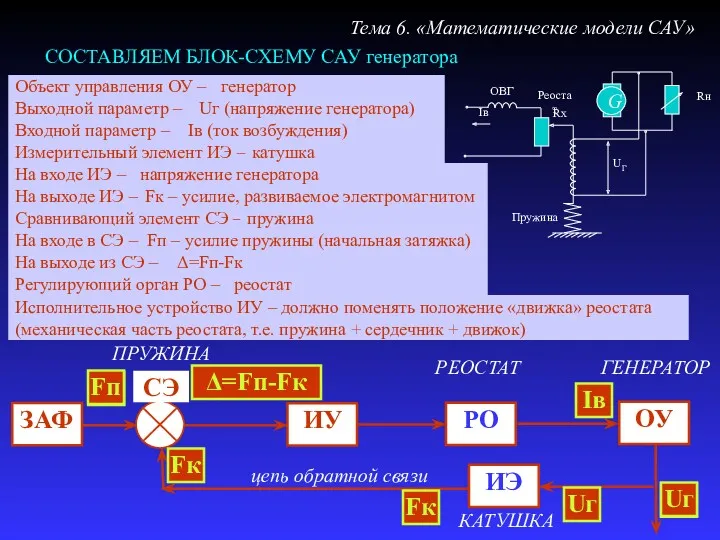
- 29. Выходной параметр – СОСТАВЛЯЕМ БЛОК-СХЕМУ САУ генератора Тема 6. «Математические модели САУ» Uг (напряжение генератора) Объект
- 30. ЗАМЕНЯЕМ ЭЛЕМЕНТЫ АВТОМАТИКИ ТИПОВЫМИ ДИНАМИЧЕСКИМИ ЗВЕНЬЯМИ Тема 6. «Математические модели САУ» Объект управления ОУ: Катушка –
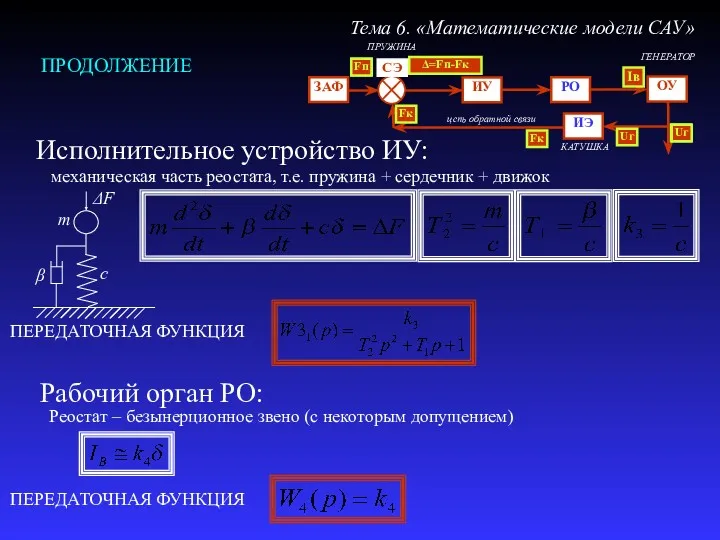
- 31. ПРОДОЛЖЕНИЕ Тема 6. «Математические модели САУ» Исполнительное устройство ИУ: Реостат – безынерционное звено (с некоторым допущением)
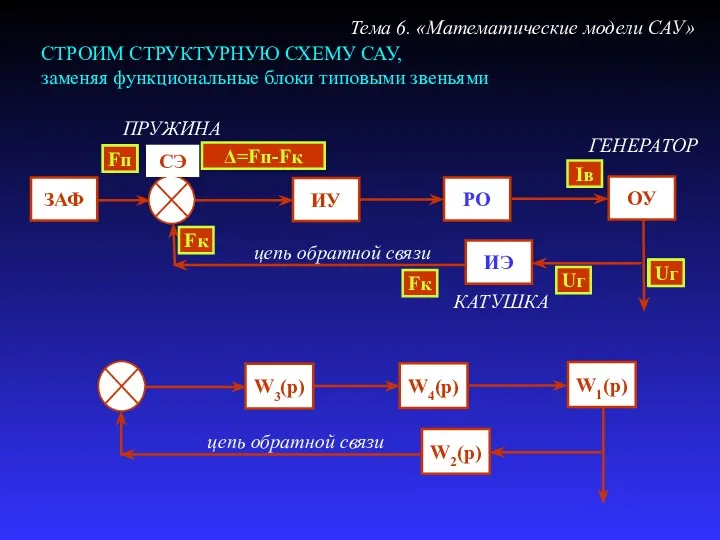
- 32. СТРОИМ СТРУКТУРНУЮ СХЕМУ САУ, заменяя функциональные блоки типовыми звеньями Тема 6. «Математические модели САУ» W3(p) W1(p)
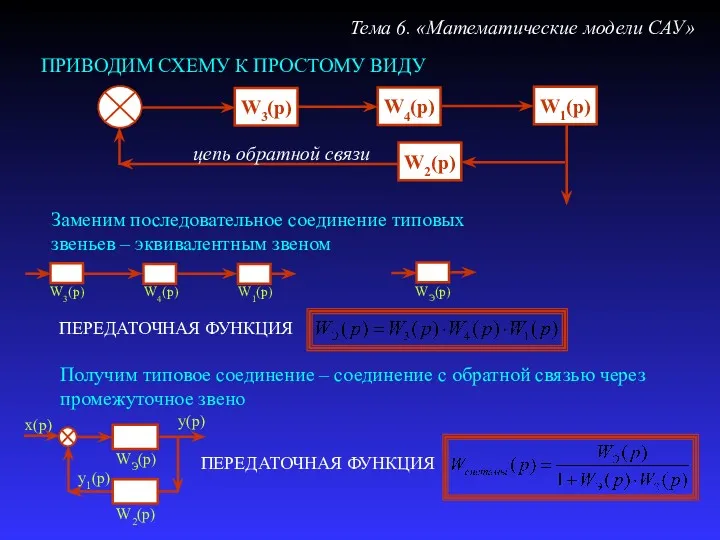
- 33. ПРИВОДИМ СХЕМУ К ПРОСТОМУ ВИДУ Тема 6. «Математические модели САУ» Получим типовое соединение – соединение с
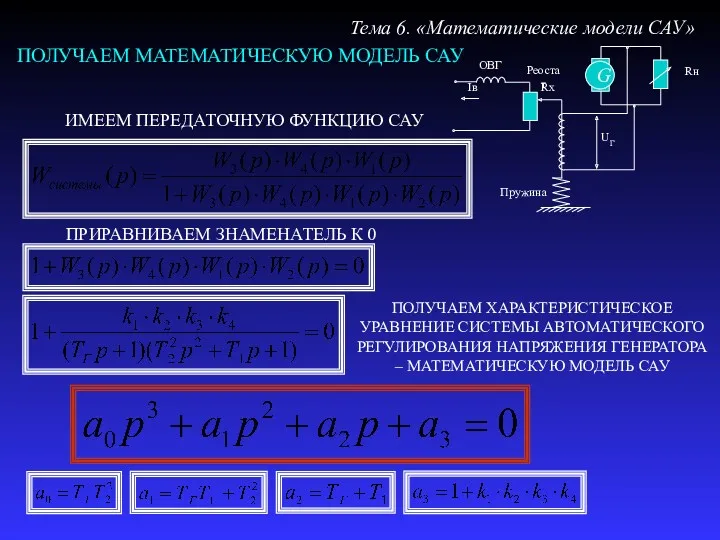
- 34. ПОЛУЧАЕМ МАТЕМАТИЧЕСКУЮ МОДЕЛЬ САУ Тема 6. «Математические модели САУ» ИМЕЕМ ПЕРЕДАТОЧНУЮ ФУНКЦИЮ САУ ПРИРАВНИВАЕМ ЗНАМЕНАТЕЛЬ К
- 35. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ Тема 6. «Математические модели САУ» МАТЕМАТИЧЕСКУЮ МОДЕЛЬ СИСТЕМЫ УПРАВЛЕНИЯ ПРМИЕНЯЮТ ПРИ ОЦЕНКЕ УСТОЙЧИВОСТИ
- 36. Тема 6.1 УСТОЙЧИВОСТЬ АВТОМАТИЧЕСКИХ СИСТЕМ Тема 6. «Математические модели САУ»
- 37. Устойчивость – свойство возвращаться в состояние устойчивого равновесия после снятия возмущения, нарушевшего равновесное состояние. Тема 6.
- 38. Метод динамических характеристик Тема 6. «Математические модели САУ» t Δy 1 2 3 4 1 –
- 39. Метод корней характеристического уравнения Тема 6. «Математические модели САУ» ИСПОЛЬЗУЮТ ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ – МАТЕМАТИЧЕСКУЮ МОДЕЛЬ САУ
- 40. Специальные критерии устойчивости систем Тема 6. «Математические модели САУ» Алгебраические критерии: критерий Гурвица, критерий Раусса Частотный
- 41. Критерий Гурвица Тема 6. «Математические модели САУ» ИЗ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ФОРМИРУЕМ ДИАГОНАЛЬНЫЙ МИНОР заполним диагональ минора
- 42. Критерий Раусса Тема 6. «Математические модели САУ» СОСТАВИМ СПЕЦИАЛЬНУЮ ТАБЛИЦУ первая строка заполняется коэффициентами с четными
- 43. Критерий Михайлова Тема 6. «Математические модели САУ» Запишем уравнение в форме полинома через оператор Лапласса четные
- 44. Точки пересечения с осями комплексной плоскости Тема 6. «Математические модели САУ» Пересечение с мнимой осью ПУСТЬ
- 46. Скачать презентацию
































 Решение задач на составление уравнений
Решение задач на составление уравнений График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Конус. Конусы вокруг нас
Конус. Конусы вокруг нас Презентации Состав чисел от 1 до 10
Презентации Состав чисел от 1 до 10 Тела вращения. Площади поверхности и объёмы
Тела вращения. Площади поверхности и объёмы Множества. Последовательность
Множества. Последовательность Игра Что? Где? Когда? по математике. (10 класс)
Игра Что? Где? Когда? по математике. (10 класс) Урок математики в 1 классе Двузначные числа. Чтение и запись.Закрепление УМК Гармония
Урок математики в 1 классе Двузначные числа. Чтение и запись.Закрепление УМК Гармония Длина окружности
Длина окружности ЕГЭ профиль: задание 9. Графики и функции
ЕГЭ профиль: задание 9. Графики и функции Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Презентация Арифметические диктанты 2 класс.
Презентация Арифметические диктанты 2 класс. Степени с действительным показателем. Степень с натуральным показателем
Степени с действительным показателем. Степень с натуральным показателем Сложение чисел. Сложение вида □+6, Сложение вида □+7
Сложение чисел. Сложение вида □+6, Сложение вида □+7 Контрольная работа по математике 4 класс
Контрольная работа по математике 4 класс Исследование расположения корней квадратного трехчлена
Исследование расположения корней квадратного трехчлена Комбинаторное правило умножения. Урок №2
Комбинаторное правило умножения. Урок №2 РАЗВИТИЯ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ У ДОШКОЛЬНИКОВ В СВЕТЕ РЕАЛИЗАЦИИ ФЕДЕРАЛЬНЫХ ГОСУДАРСТВЕННЫХ ОБРАЗОВАТЕЛЬНЫХ СТАНДАРТОВ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ
РАЗВИТИЯ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ У ДОШКОЛЬНИКОВ В СВЕТЕ РЕАЛИЗАЦИИ ФЕДЕРАЛЬНЫХ ГОСУДАРСТВЕННЫХ ОБРАЗОВАТЕЛЬНЫХ СТАНДАРТОВ ДОШКОЛЬНОГО ОБРАЗОВАНИЯ Случаи деления, когда делитель больше делимого
Случаи деления, когда делитель больше делимого Арифметическая прогрессия
Арифметическая прогрессия Тест по математике для 4 класса(Программа Школа России)
Тест по математике для 4 класса(Программа Школа России) Логика и основы алгоритмизации инженерных задач
Логика и основы алгоритмизации инженерных задач Математика. Изучение нового материала.
Математика. Изучение нового материала. Прогрессии и их применение в жизни
Прогрессии и их применение в жизни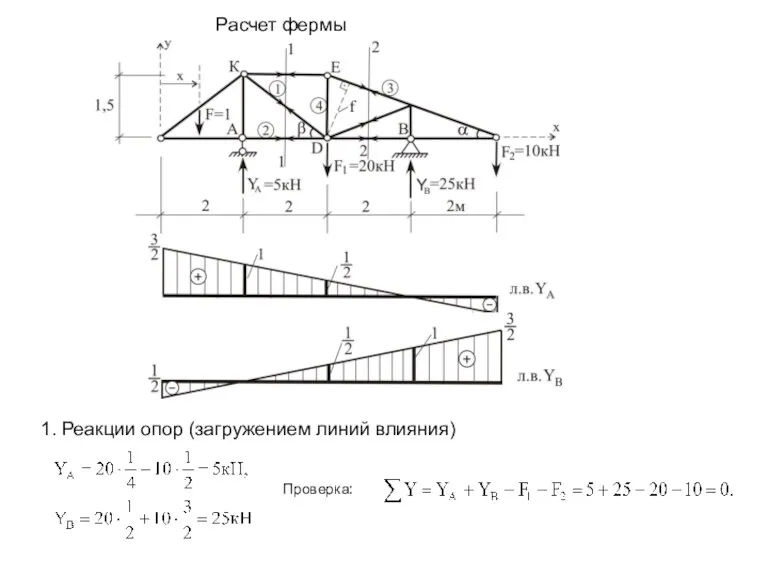 Расчет фермы
Расчет фермы Структура исследовательского проекта по математике
Структура исследовательского проекта по математике Решение дробных рациональных уравнений
Решение дробных рациональных уравнений Уравнения, приводимые к квадратным acosx +b cosx + c = 0
Уравнения, приводимые к квадратным acosx +b cosx + c = 0