Содержание
- 2. 4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ 4.1 Функция. Основные понятия и свойства 4.2 Предел функции 4.3 Непрерывность
- 3. 4. ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИЙ 4.2 Предел функции 4.2.1. Предел функции в точке 4.2.2. Односторонние пределы
- 4. 4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВА Функция y = f(x) называется бесконечно малой функцией (б.м.ф.)
- 5. 4.2.6. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ И ИХ СВОЙСТВА Сумма (разность) конечного числа б.м.ф. есть снова б.м.ф. Произведение
- 6. 4.2.7. БЕСКОНЕЧНО БОЛЬШИЕ ФУНКЦИИ И ИХ СВОЙСТВА Функция y = f(x) называется бесконечно большой функцией (б.б.ф.)
- 7. СВЯЗЬ МЕЖДУ Б.М.Ф. И Б.Б.Ф. Если f(x) - б.б.ф. при , тогда - б.м.ф. при .
- 8. 4.2.8. ТЕОРЕМА О ЕДИНСТВЕННОСТИ ПРЕДЕЛА Если предел функции y = f(x) при существует, то он единственный.
- 9. 4.2.9. ПРЕДЕЛ СЛОЖНОЙ ФУНКЦИИ Если , причём , тогда . Замечание. Это свойство позволяет использовать замену
- 10. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Вычисление предела: начинают с подстановки предельного значения x0 в функцию f(x). Если при
- 11. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Правило 1. Разделить числитель и знаменатель дроби на х в наивысшей степени. Примеры
- 12. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 13. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 14. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Правило 2. 1 способ: разделить числитель и знаменатель дроби на ( х -
- 15. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 16. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 17. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Правило 3. (функции f(x) и g(x) содержат корни) Примеры Умножить числитель и знаменатель
- 18. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 19. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 20. ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ Следствия:
- 21. ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ Следствия:
- 22. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Правило 4. (функции f(x) и g(x) содержат тригонометрические функции) Примеры Применить первый замечательный
- 23. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 24. 4.2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ α(x) и β(x) называются эквивалентными бесконечно малыми функциями при , если
- 25. 4.2.11. ЭКВИВАЛЕНТНЫЕ БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ Свойства эквивалентных б.м.ф. Если α(x) ~ β(x) и β(x) ~ γ(x)
- 26. 4.2.10. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ Примеры
- 28. Скачать презентацию

























 В стране сенсорики
В стране сенсорики Алгоритм сложения трёхзначных чисел
Алгоритм сложения трёхзначных чисел Среднее арифметическое чисел
Среднее арифметическое чисел Округление десятичных дробей. Урок математики в 5 классе
Округление десятичных дробей. Урок математики в 5 классе Графики уравнений, содержащих модули
Графики уравнений, содержащих модули Умножение дробей, умножение дроби на число, умножение смешанных чисел
Умножение дробей, умножение дроби на число, умножение смешанных чисел Числовая окружность на координатной плоскости
Числовая окружность на координатной плоскости Числа 0 - 10
Числа 0 - 10 Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Занятие по познавательному развитию Мешок яблок Диск
Занятие по познавательному развитию Мешок яблок Диск Матрицы, определители, Формулы Крамера
Матрицы, определители, Формулы Крамера Алгебра и начала математического анализа
Алгебра и начала математического анализа Квадратное уравнение и его корни
Квадратное уравнение и его корни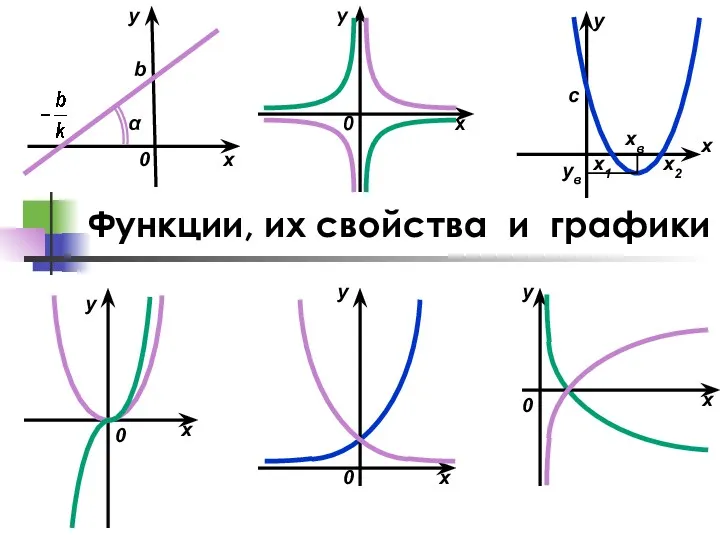 Функции, их свойства и графики
Функции, их свойства и графики Выборочное наблюдение
Выборочное наблюдение конспект урока с презентацией 3 класс
конспект урока с презентацией 3 класс Сложение и вычитание дробей с одинаковыми знаменателями. Урок математики в 5 классе
Сложение и вычитание дробей с одинаковыми знаменателями. Урок математики в 5 классе Скалярное произведение векторов. 10 класс
Скалярное произведение векторов. 10 класс Интерактивный тренажёр. Состав чисел в пределах 10
Интерактивный тренажёр. Состав чисел в пределах 10 Решение задач по теме векторы
Решение задач по теме векторы Слагаемые. Сумма
Слагаемые. Сумма тест по математике № 1 - 1 класс
тест по математике № 1 - 1 класс Краски радуги Диск
Краски радуги Диск Теорема Дезарга
Теорема Дезарга Развивающая игра по математике для младшего дошкольного возраста
Развивающая игра по математике для младшего дошкольного возраста Арифметический квадратный корень
Арифметический квадратный корень Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника Смешанные числа. Урок математики, 5 класс
Смешанные числа. Урок математики, 5 класс