Содержание
- 2. ОПРЕДЕЛЕНИЕ. Производной функции y = f(x) в точке x0 называется предел отношения приращения функции в этой
- 3. ТЕОРЕМА 1 (необходимое и достаточное условие существо- вания производной). Функция y = f(x) имеет производную в
- 4. Соответствие x0 → f ′(x0) является функцией, определенной на множестве D1⊆ D(f). Ее называют производной функции
- 5. 2. Физический и геометрический смысл производной 1) Физический смысл производной. Если функция y = f(x) и
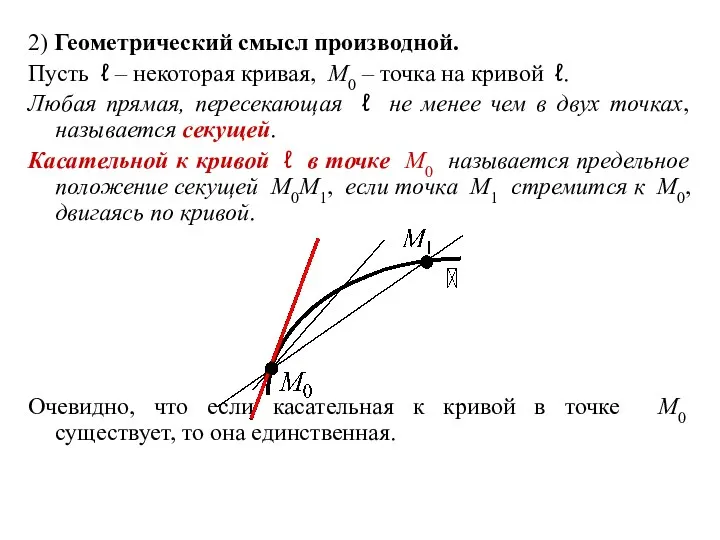
- 6. 2) Геометрический смысл производной. Пусть ℓ – некоторая кривая, M0 – точка на кривой ℓ. Любая
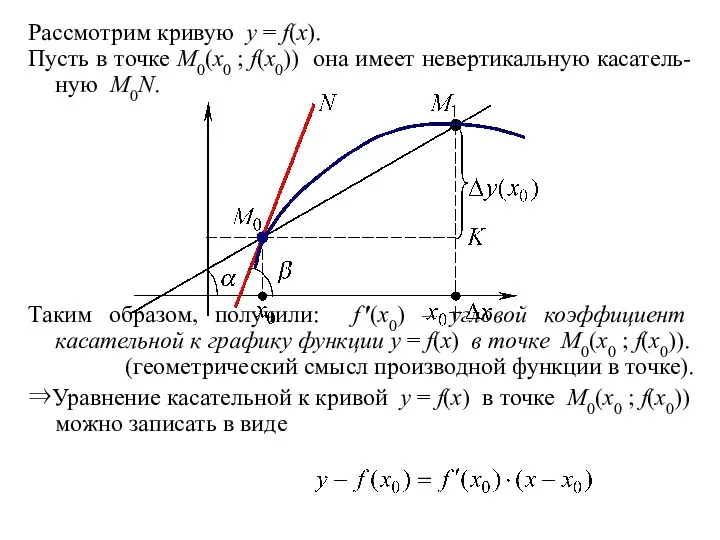
- 7. Рассмотрим кривую y = f(x). Пусть в точке M0(x0 ; f(x0)) она имеет невертикальную касатель- ную
- 8. Замечания. 1) Прямая, проходящая через точку M0 перпендикулярно касательной, проведенной к кривой в точке M0, называется
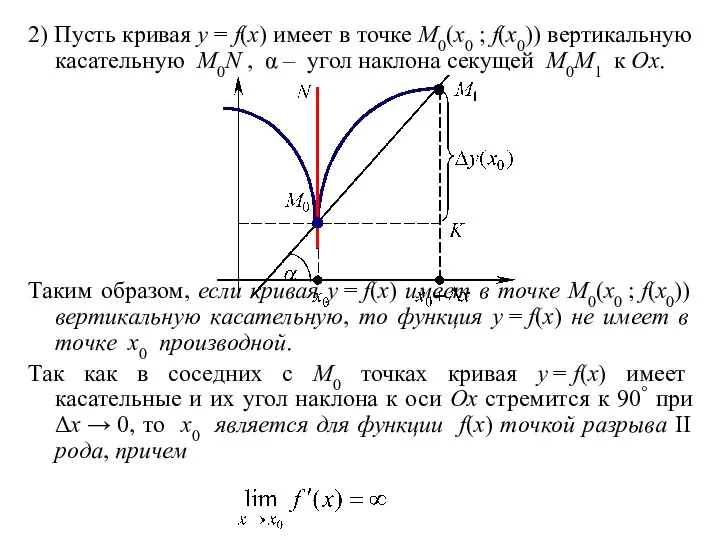
- 9. 2) Пусть кривая y = f(x) имеет в точке M0(x0 ; f(x0)) вертикальную касательную M0N ,
- 10. 3. Правила дифференцирования 1) Производная константы равна нулю, т.е. C ′ = 0, где С –
- 11. , где С – константа. Говорят: «константа выносится за знак производной». 5) Производная дроби находится по
- 12. УПРАЖНЕНИЯ. 1) Зная, что (sinx) ′ = cosx, (cosx) ′ = –sinx, (ex) ′ = ex,
- 14. Скачать презентацию








 Бөлшек сандардың ондық жазылуы
Бөлшек сандардың ондық жазылуы Игра Морской бой по математике
Игра Морской бой по математике Сравнение, сложение и вычитание десятичных дробей
Сравнение, сложение и вычитание десятичных дробей Движение. Симметрия. Поворот. Параллельный перенос. Осевая симметрия. Центральная симметрия
Движение. Симметрия. Поворот. Параллельный перенос. Осевая симметрия. Центральная симметрия Неделя математики посвящена 222-летию со дня рождения Н.И. Лобачевского. Математическая игра
Неделя математики посвящена 222-летию со дня рождения Н.И. Лобачевского. Математическая игра Сфера и шар
Сфера и шар Приёмы устных вычислений вида 260+310, 670-140
Приёмы устных вычислений вида 260+310, 670-140 Знакомство с цифрой 0
Знакомство с цифрой 0 Решение уравнения cosx = a. Понятие арккосинуса числа
Решение уравнения cosx = a. Понятие арккосинуса числа Линейное программирование
Линейное программирование Логические задачи для 1 класса
Логические задачи для 1 класса Что такое дробь?
Что такое дробь? Потреба у паліативній допомозі в Україні: розбіжності у статистичних даних
Потреба у паліативній допомозі в Україні: розбіжності у статистичних даних Квадратичная функция, ее график и свойства
Квадратичная функция, ее график и свойства Презентация к уроку математики по теме Дроби 4 класс
Презентация к уроку математики по теме Дроби 4 класс Делители и кратные
Делители и кратные Применение логарифмов в специальности. ТОРАТ
Применение логарифмов в специальности. ТОРАТ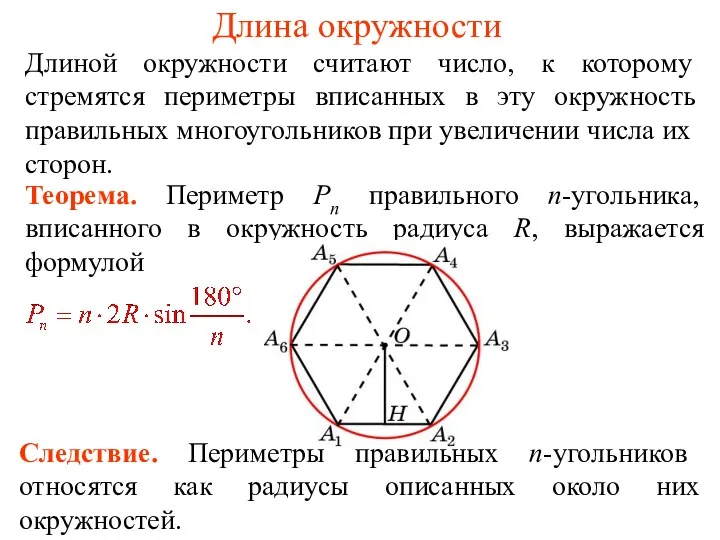 Длина окружности
Длина окружности Диаграммы. 6 класс
Диаграммы. 6 класс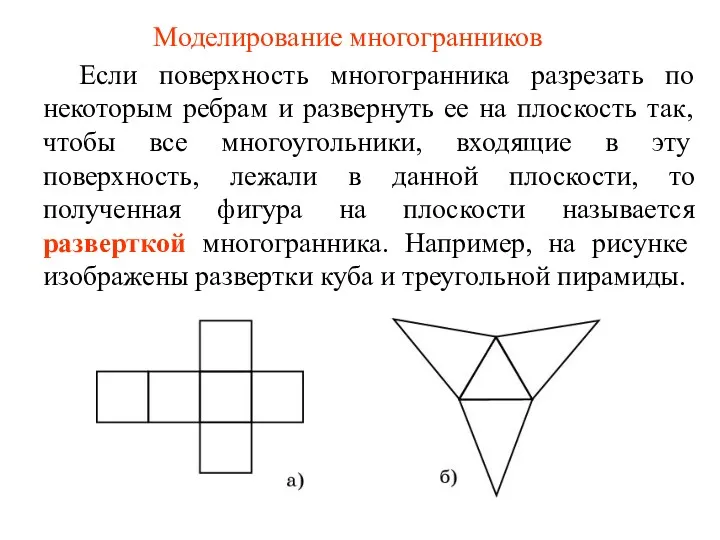 Моделирование многогранников
Моделирование многогранников Развитие у детей раннего возраста восприятия цвета, формы и величины
Развитие у детей раннего возраста восприятия цвета, формы и величины Нод по сенсорному развитию Паровозик из Ромашкова
Нод по сенсорному развитию Паровозик из Ромашкова Основы алгебры логики (Алгебра высказываний или двоичная алгебра)
Основы алгебры логики (Алгебра высказываний или двоичная алгебра) Графики тригонометрических функций
Графики тригонометрических функций Основы квалиметрии. Общие сведения о методологии квалиметрии
Основы квалиметрии. Общие сведения о методологии квалиметрии Подобные слагаемые
Подобные слагаемые Урок+презентация Сложение и вычитание вида + (-) 2,3
Урок+презентация Сложение и вычитание вида + (-) 2,3 Числа от 1 до 10
Числа от 1 до 10