Содержание
- 2. Линейное программирование Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах
- 3. Задачи линейного программирования можно решить аналитическим путем и графическим методом. В геометрии есть такое понятие, как
- 4. Симплекс-метод Идея метода симплекс-таблиц заключается в целенаправленном переборе вершин симплекса. Для начало перебора необходимо выбрать опорную
- 5. Задача линейного программирования записывается следующим образом:
- 6. Аналитический метод решения задач ЛП: 1. Найти вершины ОДР. 2. Определить значения целевой функции в вершинах.
- 7. Основная теорема линейного программирования Целевая функция задачи линейного программирования достигает своего экстремума (минимума или максимума) в
- 8. В том случае, когда требуется найти минимум функции можно перейти к нахождению максимума функции поскольку
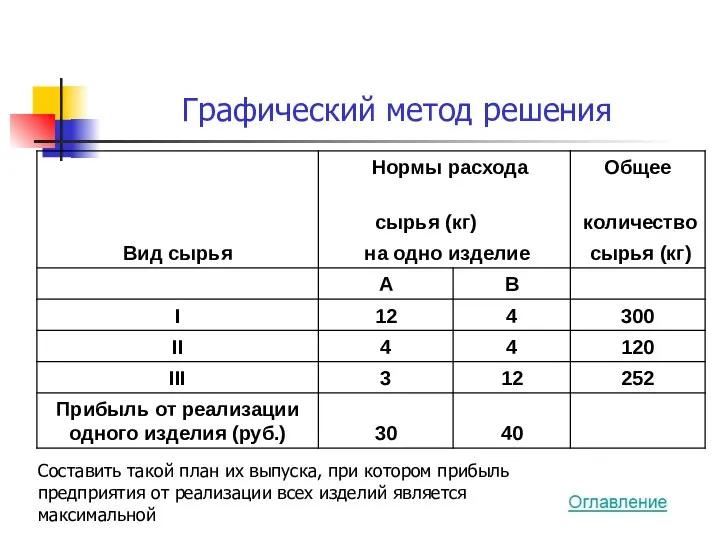
- 9. Графический метод решения Составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий
- 10. Будет изготовлено: x1 единиц изделий вида А x2 единиц изделий вида В Прибыль от их реализации
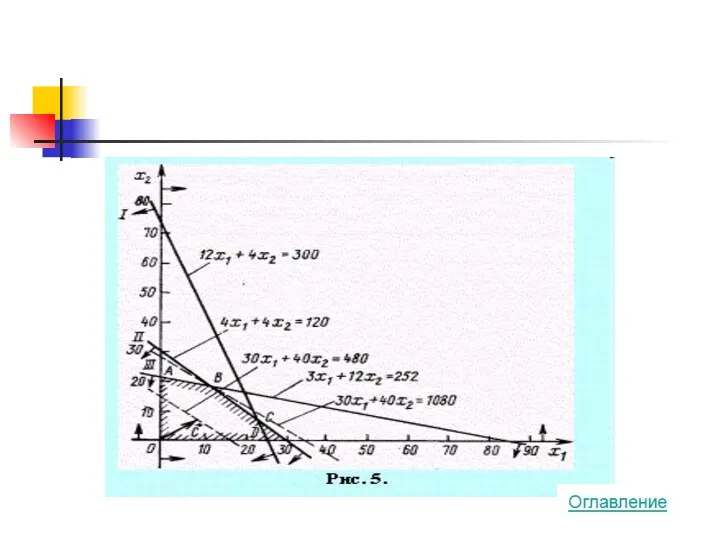
- 12. Координаты точки В и определяют план выпуска изделий А и В, при котором прибыль от их
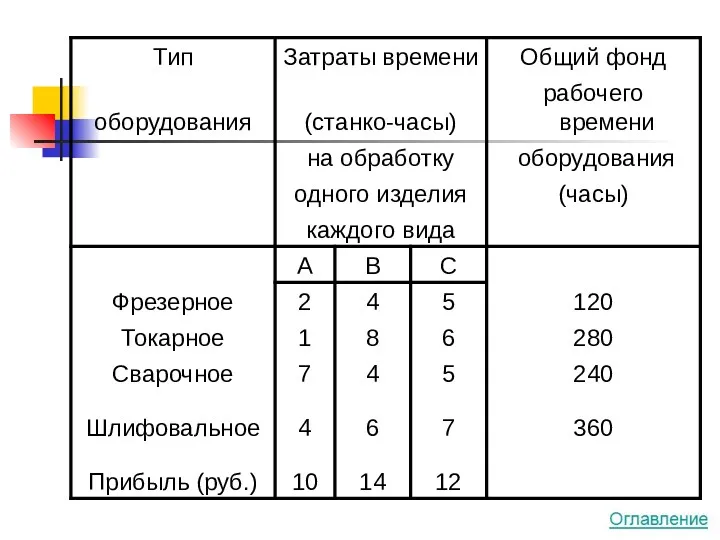
- 14. Задача на максимум Сколько изделий и какого вида следует изготовить предприятию, чтобы прибыль от их реализации
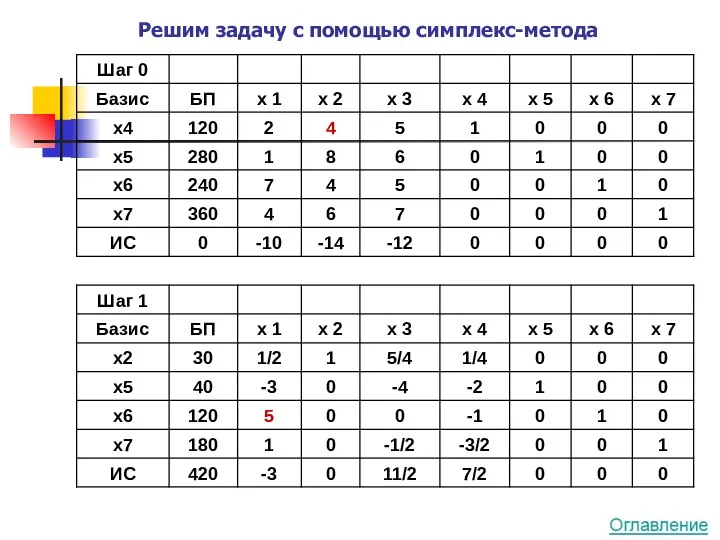
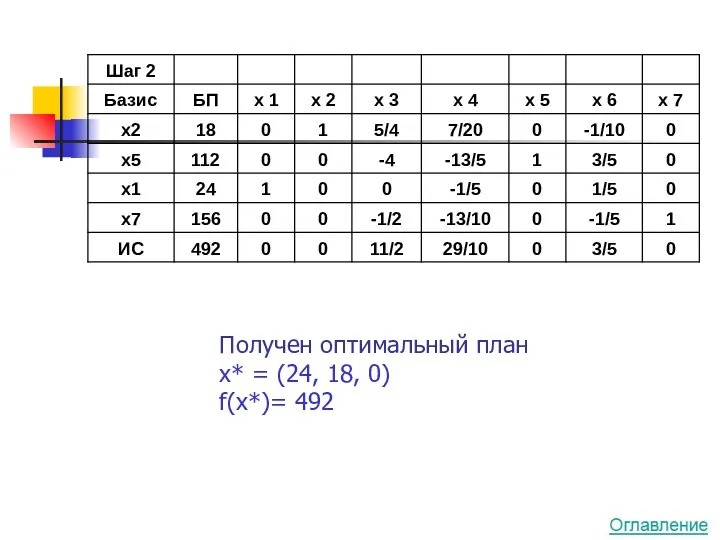
- 15. Решим задачу с помощью симплекс-метода
- 16. Получен оптимальный план x* = (24, 18, 0) f(x*)= 492
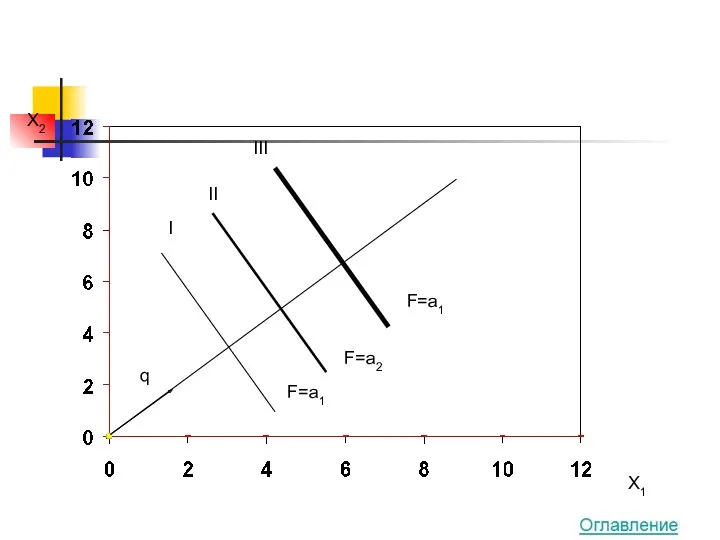
- 17. Геометрический метод решения задач линейного программирования
- 18. Основные понятия Линия уровня – линия, вдоль которой целевая функция принимает одно и то же фиксированное
- 19. q I II III F=a1 F=a2 F=a1 X2 X1
- 20. Геометрический смысл x1 x2 c1x1 + c2x2 → max a11x1 + a12x2 ≤ b1 a12x1 +
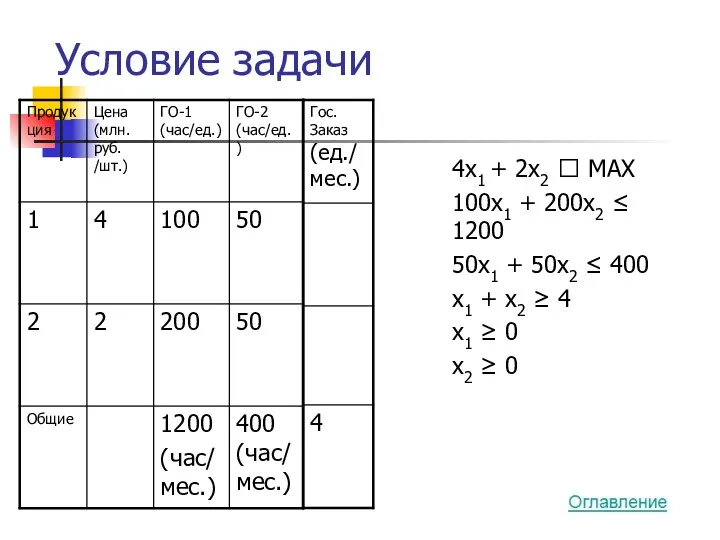
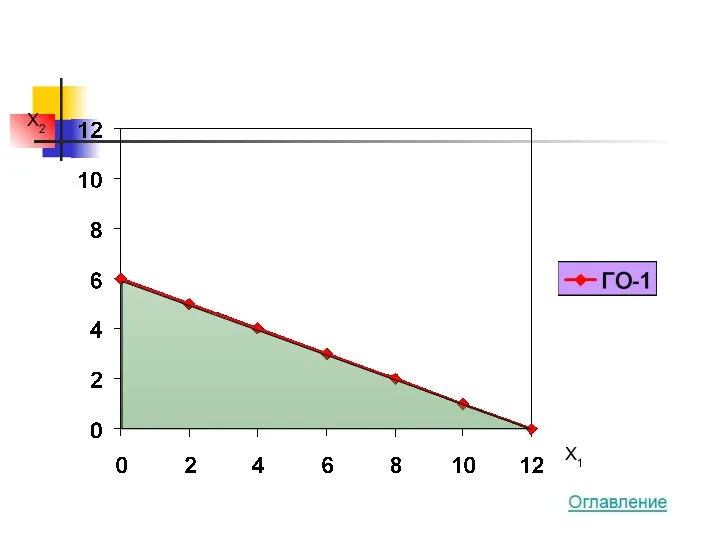
- 21. Условие задачи 4x1 + 2x2 ? MAX 100x1 + 200x2 ≤ 1200 50x1 + 50x2 ≤
- 22. X2 X1
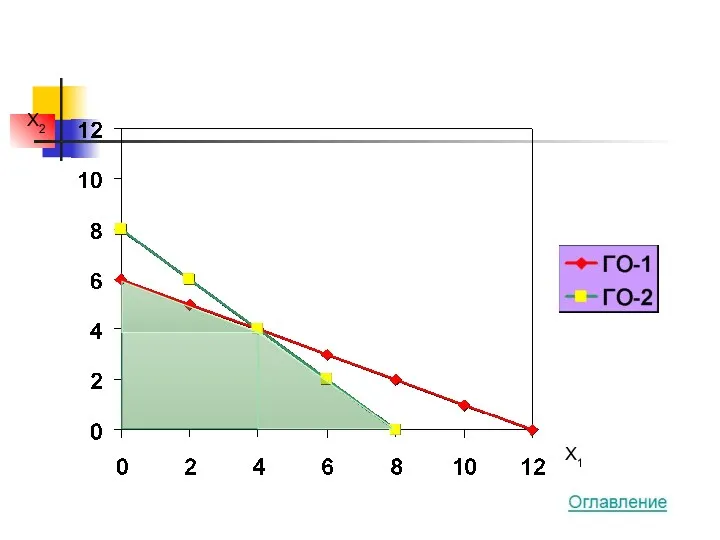
- 23. X2 X1
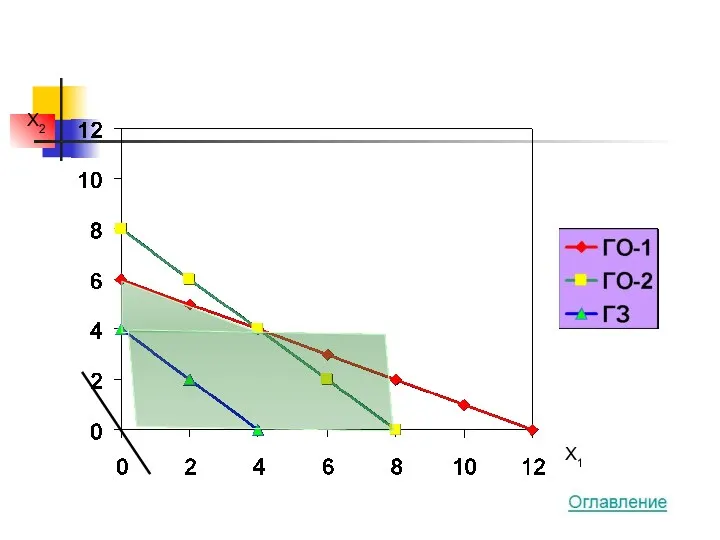
- 24. X2 X1
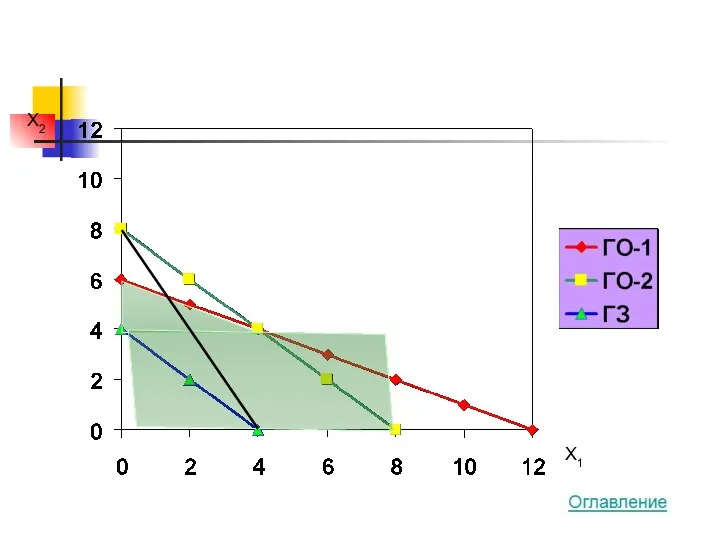
- 25. X2 X1
- 26. X2 X1
- 27. Ответ и проверка 4*8 + 2*0 ? MAX 100*8 + 200*0 ≤ 1200 50*8 + 50*0
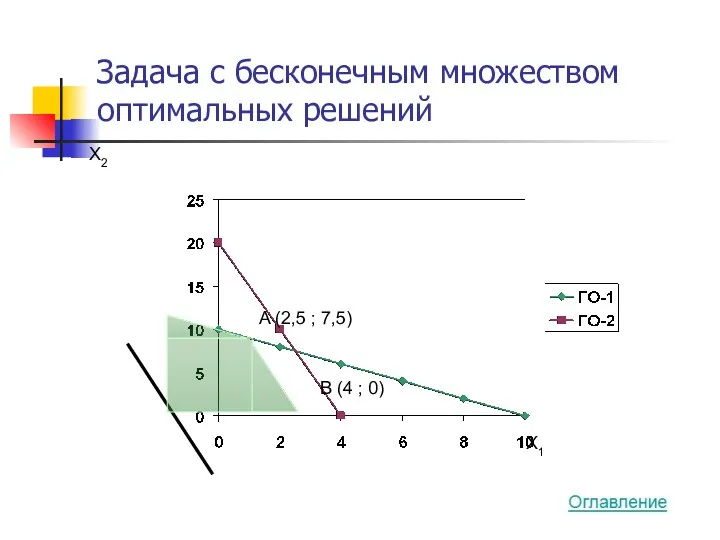
- 28. Задача с бесконечным множеством оптимальных решений X2 X1 A (2,5 ; 7,5) B (4 ; 0)
- 29. Координаты точек оптимальных решений α(2,5 ; 7,5) + (1 - α)(4 ; 0) = =(2,5α ;
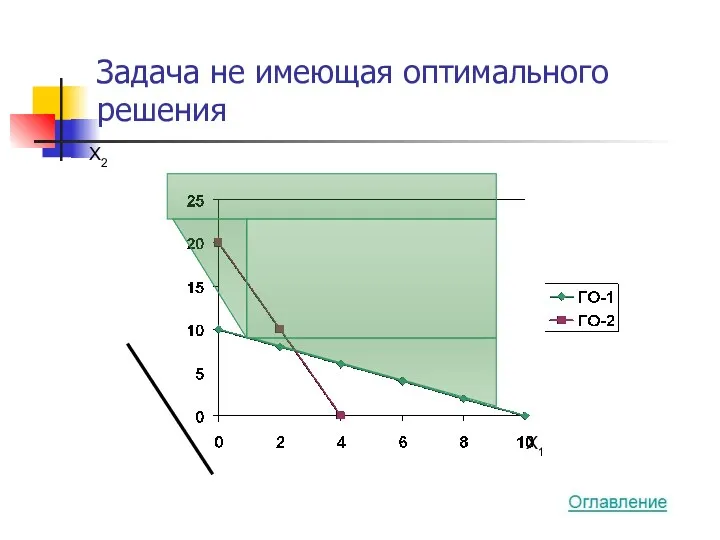
- 30. Задача не имеющая оптимального решения X2 X1
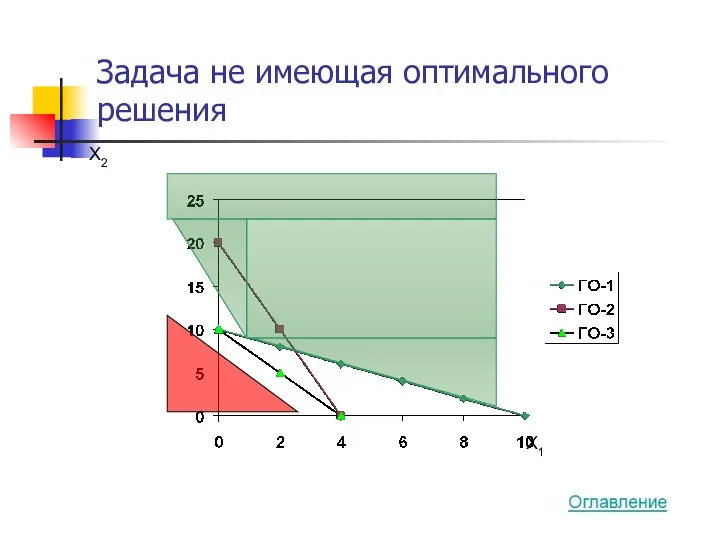
- 31. Задача не имеющая оптимального решения X2 X1
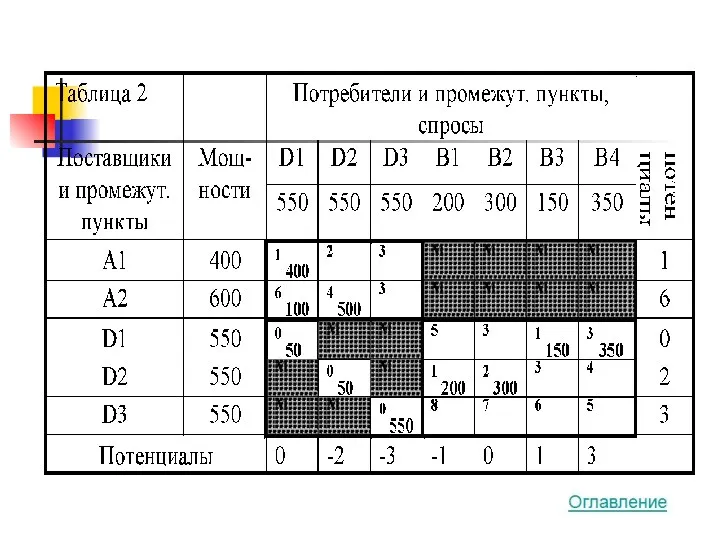
- 32. Усложнённые постановки транспортной задачи
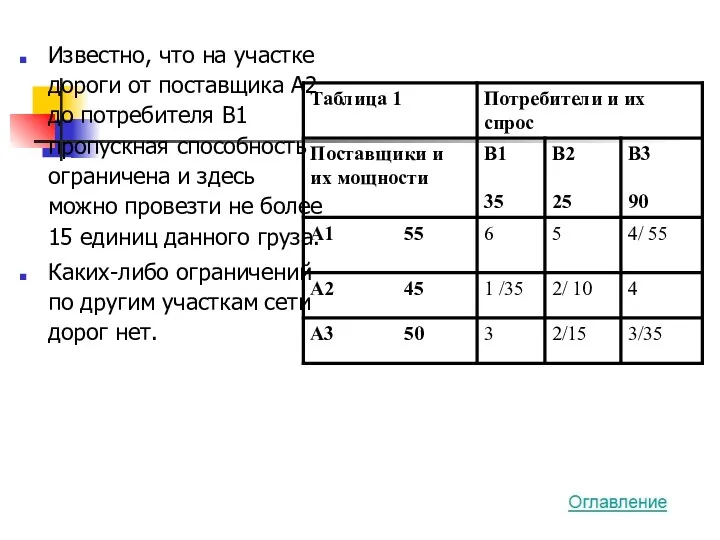
- 33. Ограничения пропускной способности: В стандартной постановке транспортной задачи предполагается, что из любого пункта по любой дороге
- 34. Известно, что на участке дороги от поставщика А2 до потребителя В1 пропускная способность ограничена и здесь
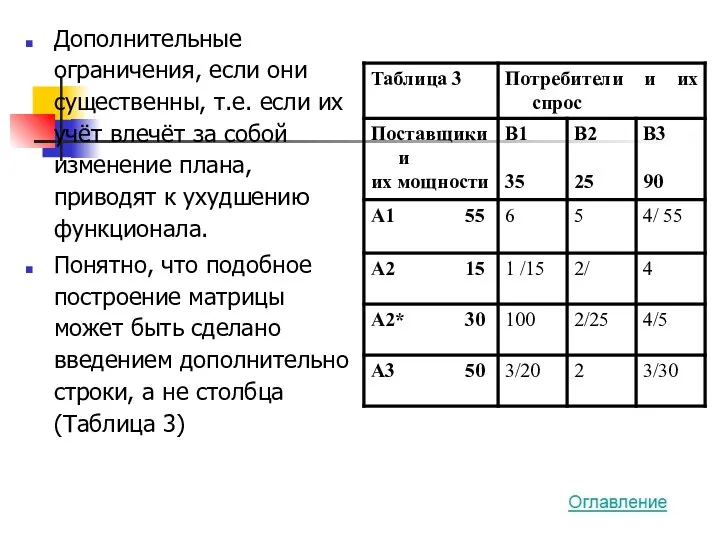
- 35. Дополнительные ограничения, если они существенны, т.е. если их учёт влечёт за собой изменение плана, приводят к
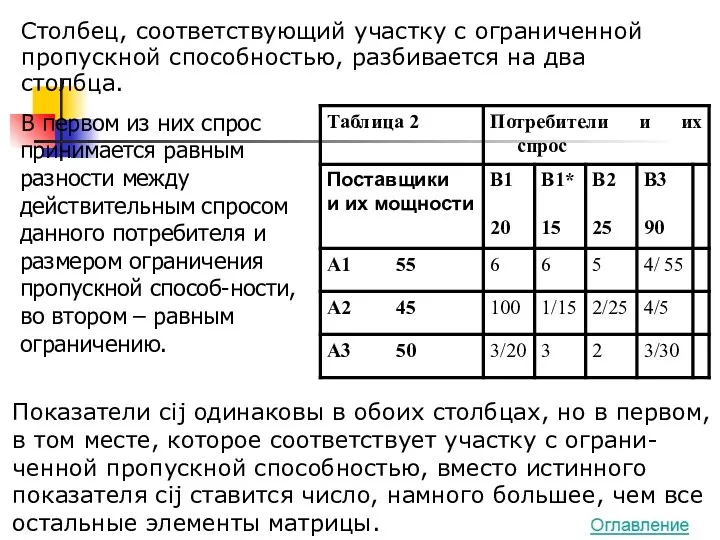
- 36. В первом из них спрос принимается равным разности между действительным спросом данного потребителя и размером ограничения
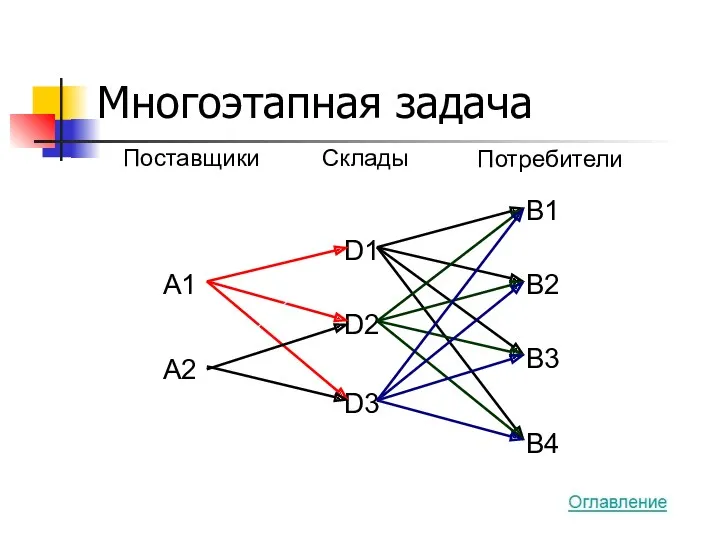
- 37. Многоэтапная задача A1 A2 D1 D2 D3 В1 В2 В3 В4 Поставщики Склады Потребители
- 38. Если суммарная ёмкость складов равна суммарной мощности и суммарному спросу потребителей ёмкость каждого склада будет использоваться
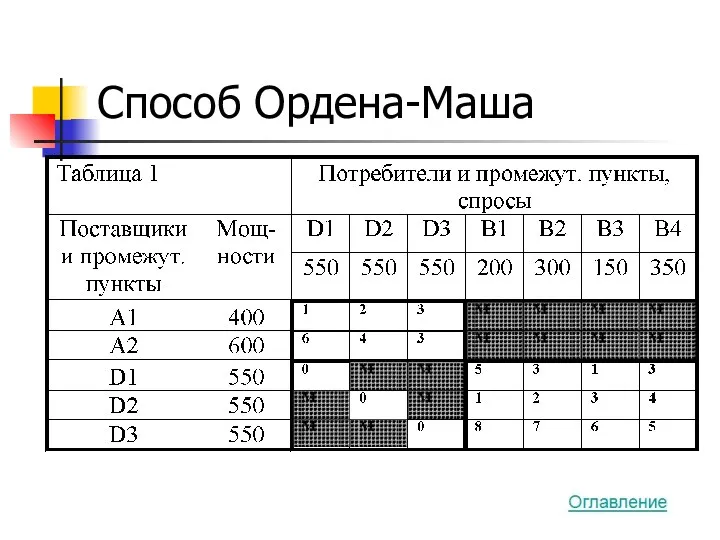
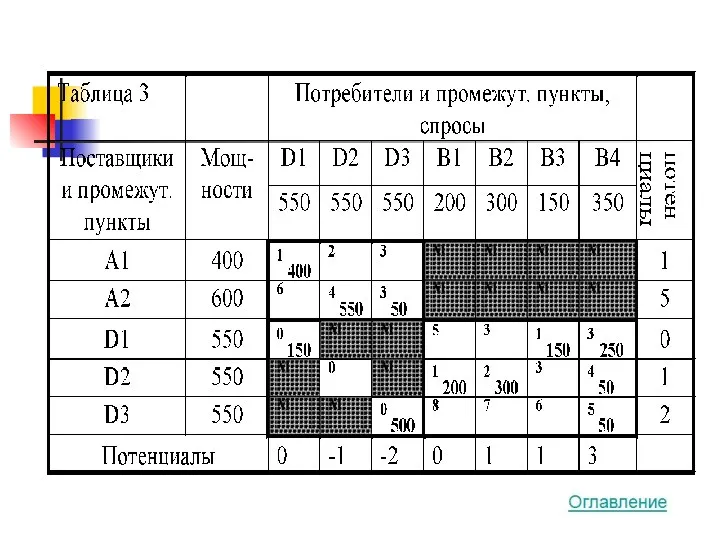
- 39. Способ Ордена-Маша
- 42. Двойственные задачи
- 43. Любая задача линейного программирования (даже не имеющая решений) имеет двойственную задачу. Прежде чем строить двойственную задачу
- 44. Правило построения двойственной задачи: Если исходная задача на max, то двойственная на min и наоборот. В
- 45. f(x) g(y) - основное неравенство двойственности Теорема1: Если исходная задача имеет оптимальный план x*, то двойственная
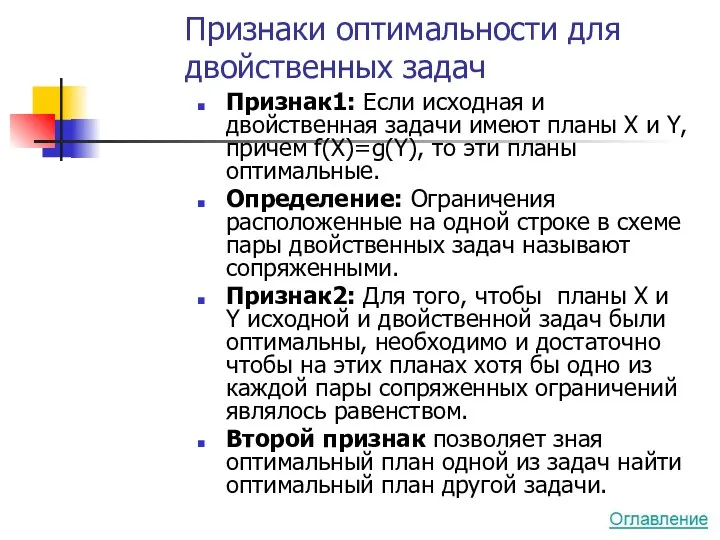
- 46. Признаки оптимальности для двойственных задач Признак1: Если исходная и двойственная задачи имеют планы X и Y,
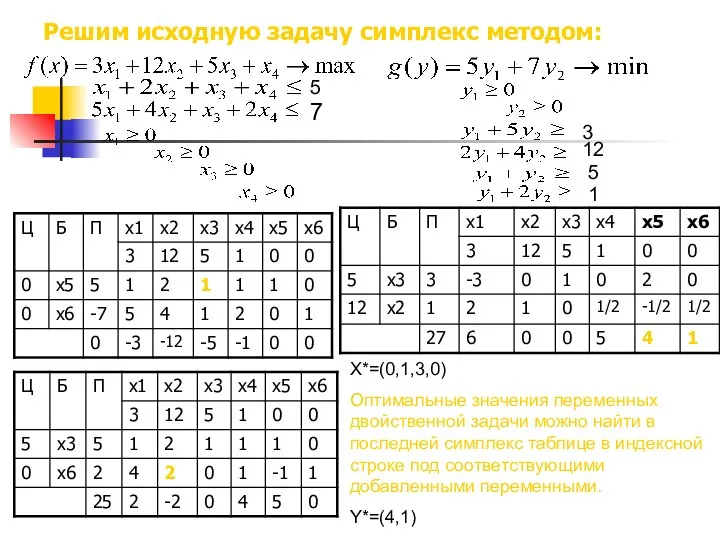
- 47. Решим исходную задачу симплекс методом: 5 7 3 12 5 1 X*=(0,1,3,0) Оптимальные значения переменных двойственной
- 48. Закрытая транспортная задача. Метод потенциалов
- 49. Определение Закрытая транспортная задача – задача о перевозке однородной продукции, когда имеется m поставщиков, для которых
- 50. Постановка задачи Требуется составить план перевозок – указать, какое кол-во продукции нужно перевезти от каждого поставщика
- 51. Обозначения bi – множество поставщиков aj – множество потребителей сij – цены перевозок единицы товара от
- 52. Целевая функция f(X)=ΣΣcijxij→min
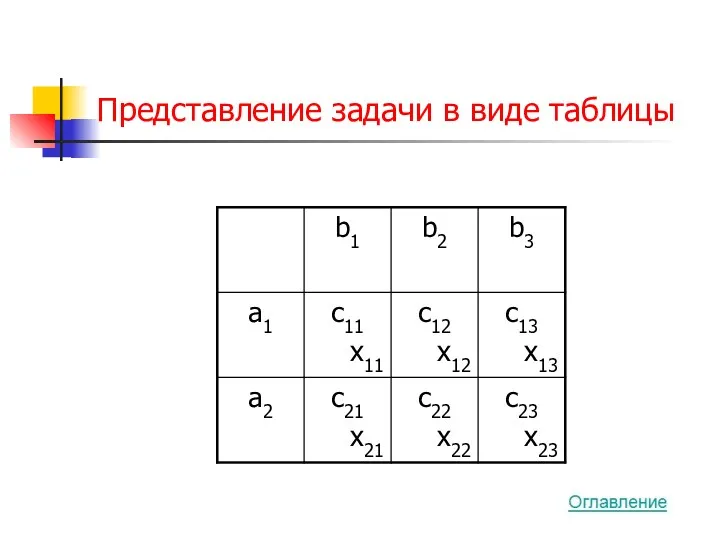
- 53. Представление задачи в виде таблицы
- 54. Двойственная задача
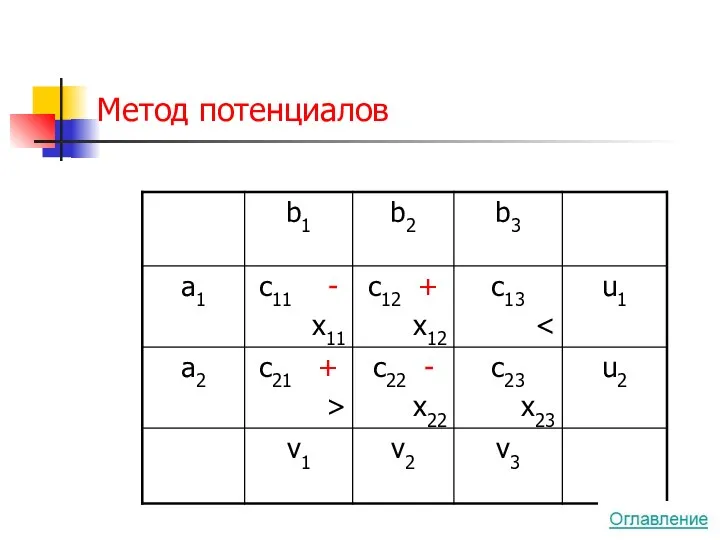
- 55. Метод потенциалов
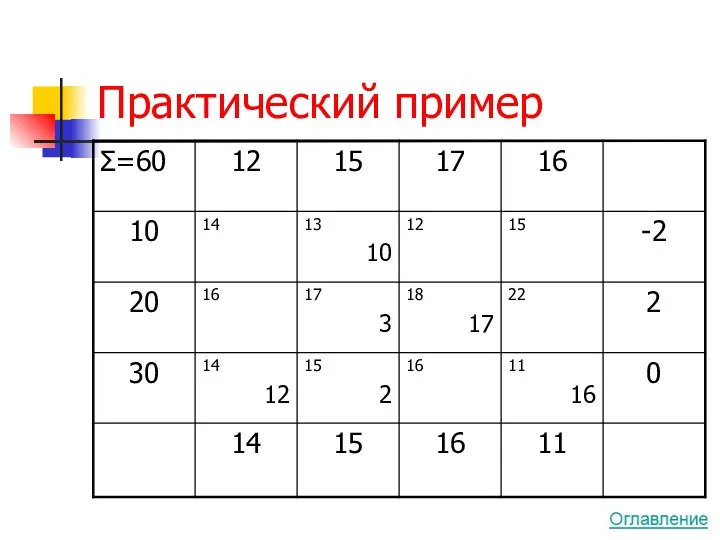
- 56. Практический пример
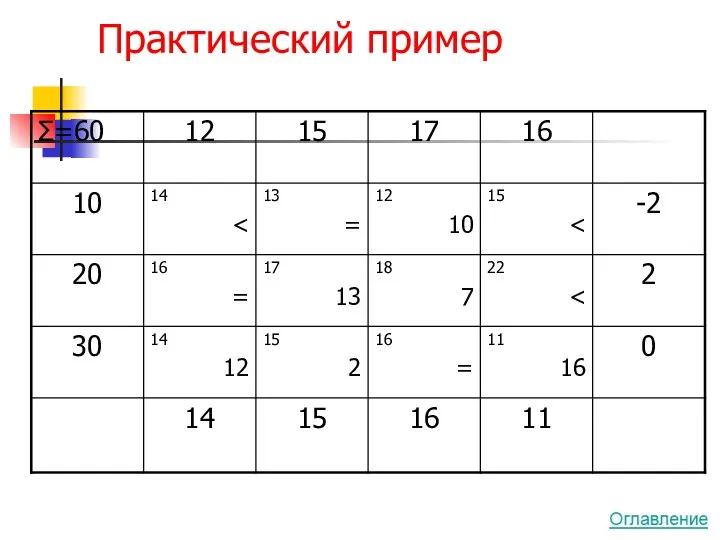
- 57. Практический пример
- 58. Практический пример
- 59. Практический пример
- 60. Практический пример
- 62. Скачать презентацию































 Transactions and database integrity
Transactions and database integrity Округление чисел до десятков, сотен. 5 класс
Округление чисел до десятков, сотен. 5 класс Математика. 4 класс. Устный счет.
Математика. 4 класс. Устный счет. Франсуа Виет
Франсуа Виет Имитационное моделирование. Примеры математических моделей (лекция 4)
Имитационное моделирование. Примеры математических моделей (лекция 4) Задачи Григория Остера для первоклассников.
Задачи Григория Остера для первоклассников. Абсолютные и относительные величины
Абсолютные и относительные величины Комбинаторика. 5 класс
Комбинаторика. 5 класс Основные категории и понятия статистики. Статистическое наблюдение. Лекция 1
Основные категории и понятия статистики. Статистическое наблюдение. Лекция 1 Треугольники и их виды
Треугольники и их виды Симметрия
Симметрия Разложение числа на простые множители
Разложение числа на простые множители Решение квадратных уравнений
Решение квадратных уравнений Конспект урока по математике во 2 классе
Конспект урока по математике во 2 классе Связь между бесконечно малыми и бесконечно большими величинами
Связь между бесконечно малыми и бесконечно большими величинами Проценты. Конспект и презентация к уроку математики. Диск
Проценты. Конспект и презентация к уроку математики. Диск Квадратные уравнения. Способы их решения. 8 класс
Квадратные уравнения. Способы их решения. 8 класс Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Какие дроби называются неправильными?
Какие дроби называются неправильными? Теория кривых. Формулы Сере-Френе
Теория кривых. Формулы Сере-Френе Сумма углов треугольника
Сумма углов треугольника Задачи про Хэллоуин. Загадочные ведьмы
Задачи про Хэллоуин. Загадочные ведьмы Отрезок
Отрезок Эконометрическое моделирование. (Лекции 5, 6, 7)
Эконометрическое моделирование. (Лекции 5, 6, 7) Элементы комбинаторики
Элементы комбинаторики Единицы длины и площади. Презентация.
Единицы длины и площади. Презентация. Устойчивость решений дискретных систем
Устойчивость решений дискретных систем Обыкновенные дроби. Деление дробей
Обыкновенные дроби. Деление дробей