Содержание
- 2. Матрицы и операции над ними Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и
- 3. или, в сокращенной записи А=( аij) i=1.. m; j=1.. n. Две матрицы А и В одного
- 4. Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца – матрицей (вектором)-столбцом. Квадратной
- 5. Классификация матриц Симметрической называется квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, равны, т.е.
- 6. Операции над матрицами Умножение матрицы на число. Произведением матрицы А на число λ называется матрица В=λА,
- 7. Умножение матриц. Умножение матриц А на матрицу В определено, когда число столбцов первой матрицы равно числу
- 8. Определители квадратной матрицы Каждой квадратной матрице А, можно поставить в соответствие вычисленное по определенным правилам число,
- 9. Определителем матрицы третьего порядка или определителем третьего порядка называется число, которое вычисляется по формуле: Δ3 =
- 10. Пусть А является квадратной матрицей n-го порядка. Минором Мij элемента аij, называется определитель (n-1)-го порядка, полученный
- 11. Теорема Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: Δ=ai1Ai1+ai2Ai2+…+ainAin.
- 12. Свойства определителей 1 Если какая-либо строка (столбец) матрицы состоит из одних нулей, то её определитель равен
- 13. Свойства определителей 6 Если элементы двух строк (столбцов) матрицы пропорциональны, то её определитель равен нулю. 7
- 14. Обратная матрица Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении этой
- 16. Алгоритм нахождения обратной матрицы Находим определитель исходной матрицы. Если │А│=0, то матрица А вырожденная и обратной
- 18. Скачать презентацию















 Статистичні помилки. Статистичні гіпотези та їх перевірка. Параметричні і непараметричні критерії перевірки
Статистичні помилки. Статистичні гіпотези та їх перевірка. Параметричні і непараметричні критерії перевірки Формирование УУД на уроках математики
Формирование УУД на уроках математики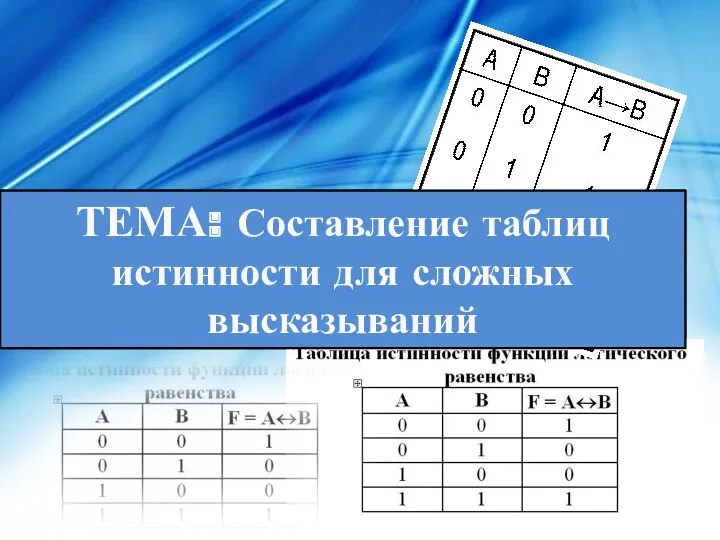 Составление таблиц истинности для сложных высказываний
Составление таблиц истинности для сложных высказываний Геометрия. Основные утверждения и теоремы
Геометрия. Основные утверждения и теоремы Формулы. Формула площади прямоугольника
Формулы. Формула площади прямоугольника Өрнектегі композиция
Өрнектегі композиция Приёмы устных вычислений в пределах 1000
Приёмы устных вычислений в пределах 1000 Тренажер по таблице умножения.
Тренажер по таблице умножения. Сравнение чисел
Сравнение чисел Контурный анализ
Контурный анализ Приёмы письменного вычитания в пределах 1000
Приёмы письменного вычитания в пределах 1000 Обучение младших школьников решению нестандартных олимпиадных задач
Обучение младших школьников решению нестандартных олимпиадных задач Принцип Дирихле
Принцип Дирихле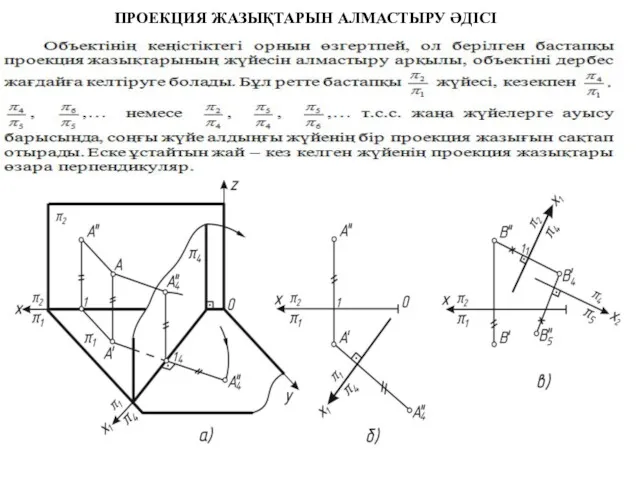 Проекция жазықтарын алмастыру әдісі
Проекция жазықтарын алмастыру әдісі Действия с рациональными числами. 13 февраля в истории
Действия с рациональными числами. 13 февраля в истории Устные задачи по теме: Взаимное расположение прямой и окружности
Устные задачи по теме: Взаимное расположение прямой и окружности Отношения и пропорции
Отношения и пропорции Август Ада Лавлейс
Август Ада Лавлейс Умножение и деление. Задачи
Умножение и деление. Задачи Числа 1 - 4
Числа 1 - 4 Точка, линия, прямая и кривая линии. Число 2. Цифра 2
Точка, линия, прямая и кривая линии. Число 2. Цифра 2 Геометрические тела и их изображение
Геометрические тела и их изображение Похідна складеної функції
Похідна складеної функції Мы за здоровый образ жизни. Устный счет
Мы за здоровый образ жизни. Устный счет Конкурс Математическое кафе для учащихся 7-8 классов
Конкурс Математическое кафе для учащихся 7-8 классов Занимательные задания для первоклассников.
Занимательные задания для первоклассников. Определенный интеграл
Определенный интеграл Числовые промежутки. Геометрическая и аналитическая модели числового промежутка
Числовые промежутки. Геометрическая и аналитическая модели числового промежутка