Мнения о методе координат
«ЗА!»
Очень – очень советую освоить координатный, вряд ли
будет что-то
такое, что координатным не решить! Меня км спасал не один раз.
(Пользователь esclade279. Форум http://abiturient.pro)
чтобы успешно решить С2, нужно разобраться в одном универсальном
способе: - координатный способ. Все длины, углы легко находятся. -
бывший абитуриент, ныне студент (Пользователь delpaNz. Форум
http://abiturient.pro)
Ребят, решайте координатным методом С2! Так без особых знаний можно
решить почти любую задачу.(Пользователь 777Julia777
http://forum.postupim.ru)
А почему бы учителям не научить абитуру считать определители 3-го
порядка? Тогда задача на нахождение расстояния от точки до прямой и между прямыми из суперсложной и недоступной многим геометрической задачи становится простой арифметической задачкой, где главное – не наврать в счете. Конечно, ваше учительское сердце протестует против этого, стремясь всех научить геометрическим методам, но результат +2 балла все таки наиболее вероятен во втором случае. Да и в универе нет
чистой геометрии, только аналитическая.(Пользователь Марина
http://www.alexlarin.com
«против!»
С2 обчно до ужаса простая задача, которая решается в 50% случаев в уме.
Так что метод координат тут не рационален. С4 иногда можно порешать
этим методом, но чаще нет. (Пользователь Hellko. Форум
http://forum.postupim.ru)



















 Элементы комбинаторики в школьном курсе математики
Элементы комбинаторики в школьном курсе математики Статистическая обработка данных
Статистическая обработка данных Презентация Состав 6 1 класс УМК Гармония
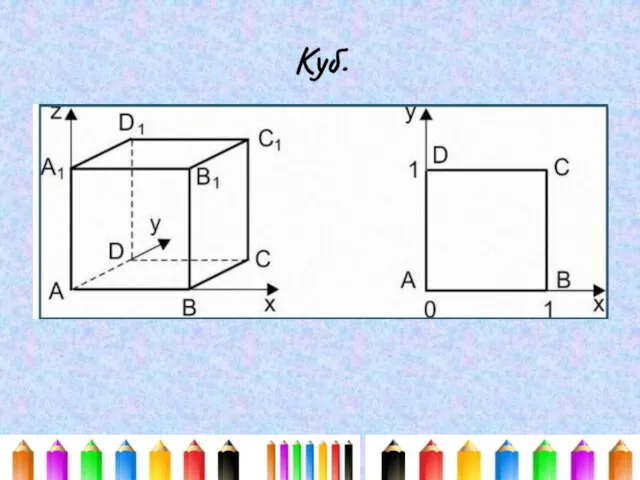
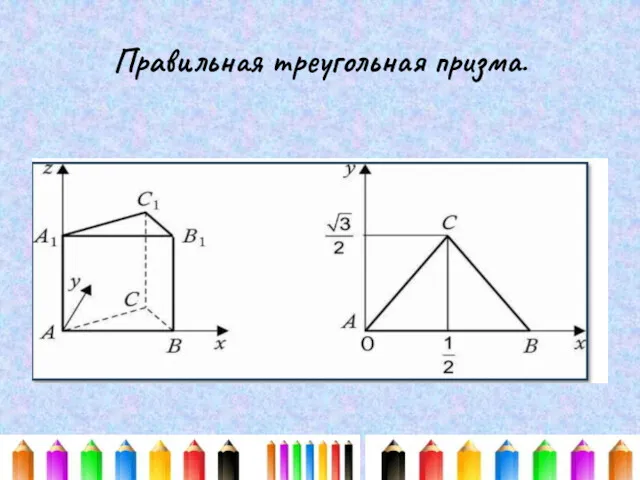
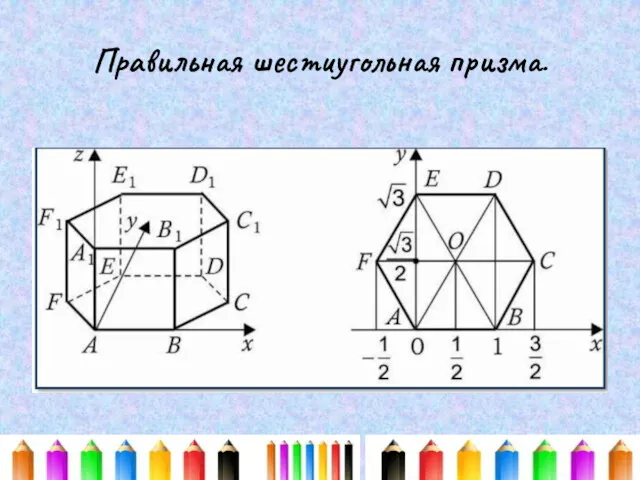
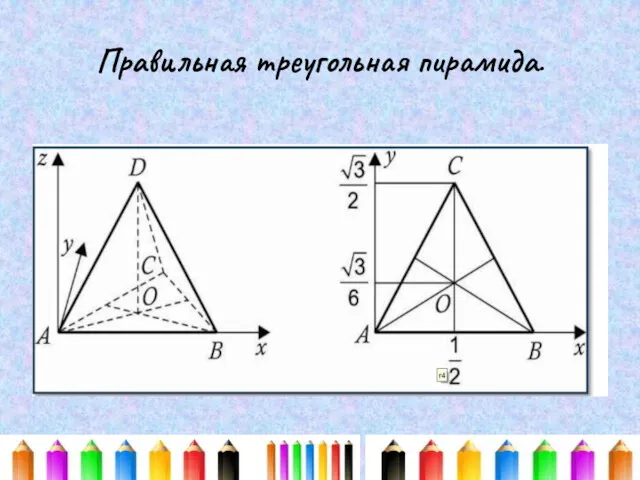
Презентация Состав 6 1 класс УМК Гармония Метод координат. Вспоминаем, повторяем, систематизируем
Метод координат. Вспоминаем, повторяем, систематизируем Методические особенности курса алгебры основной школы
Методические особенности курса алгебры основной школы Численное моделирование. Метод наименьших квадратов. (Лекция 7)
Численное моделирование. Метод наименьших квадратов. (Лекция 7) Тема урока: Нумерация трёхзначных чисел
Тема урока: Нумерация трёхзначных чисел Итоговое повторение по курсу Алгебра и начала анализа 10 класс
Итоговое повторение по курсу Алгебра и начала анализа 10 класс Творческое объединение Планета знаний. Как террористы крушат самолеты
Творческое объединение Планета знаний. Как террористы крушат самолеты Презентация к занятию по ФЭМП в старшей группе, с использованием деятельностного метода Встреча с в зайчиком
Презентация к занятию по ФЭМП в старшей группе, с использованием деятельностного метода Встреча с в зайчиком События. Вероятность. Теоремы сложения и умножения вероятностей
События. Вероятность. Теоремы сложения и умножения вероятностей Лекция 3.2. Криволинейные интегралы. Независимость криволинейного интеграла от пути интегрирования
Лекция 3.2. Криволинейные интегралы. Независимость криволинейного интеграла от пути интегрирования Начальный анализ статистической информации на основе группировки данных
Начальный анализ статистической информации на основе группировки данных Умножение натуральных чисел
Умножение натуральных чисел Своя игра. Готовимся к ОГЭ
Своя игра. Готовимся к ОГЭ Интерактивный тренажер Показательные и логарифмические уравнения
Интерактивный тренажер Показательные и логарифмические уравнения Презентация к уроку математики по теме: Сложение с числом 10. 1класс УМК Перспективная начальная школа.
Презентация к уроку математики по теме: Сложение с числом 10. 1класс УМК Перспективная начальная школа. Урок математики в 1 классе по теме: Задача
Урок математики в 1 классе по теме: Задача Понятие, задачи корреляционно-регрессионного анализа и моделирования
Понятие, задачи корреляционно-регрессионного анализа и моделирования Модели числового неравенства. Числовые промежутки
Модели числового неравенства. Числовые промежутки презентация к уроку по математике на тему Периметр многоугольника
презентация к уроку по математике на тему Периметр многоугольника 6. Уравнение окружности
6. Уравнение окружности Конспект урока математики
Конспект урока математики Решение задач на проценты в торговле
Решение задач на проценты в торговле Построение графика квадратичной функции
Построение графика квадратичной функции Системы линейных уравнений с двумя переменными. Графический способ решения
Системы линейных уравнений с двумя переменными. Графический способ решения Числовые и буквенные выражения
Числовые и буквенные выражения Ch8: Hypothesis Testing (2 Samples)
Ch8: Hypothesis Testing (2 Samples)