Многочлены презентация

Многочлены от одной переменной
р(x) = anxn + an-1xn-1 +…+ a3x3 + a2x2 + a1x + ao
- стандартный вид многочлена р(х)
anxn – старший член многочлена р(х)
an – коэффициент при старшем члене
Если an = 1, то многочлен р(х) называется приведенным
Если an ≠ 1, то многочлен р(х) называется неприведенным
aо – свободный член многочлена р(х)
n – степень многочлена

Деление многочленов
р(x) = s(x) ⋅ q(x)
Говорят, что многочлен р(х) делится на многочлен s(x), если существует такой многочлен q(x), что выполняется тождество
p(x) – делимое (или кратное)
s(x) – делитель
q(x) – частное

Деление многочленов
х2 + 5
х3 + 5х
−
− 3х2 − 15
х
− 3х2 − 15
0
т. к. х3 − 3х2 + 5х − 15 = (х2 + 5)(х − 3), то многочлен х3 − 3х2 + 5х − 15 делится на многочлены х2 + 5 и х − 3.
Пример 1
− 3
−
х3 − 3х2 + 5х − 15

Деление многочленов с остатком
р(x) = s(x) q(x) + r(х)
Для любых двух многочленов ненулевой степени р(х) и s(x) существует пара многочленов q(x) и r(x) такая, что степень многочлена r(x) меньше степени многочлена s(x) и выполняется тождество
p(x) – делимое (или кратное)
s(x) – делитель
q(x) – неполное частное
r(x) – остаток

2х2 − х − 3
х − 2
2х2 − 4х
−
3х − 6
2х
3х − 3
3
т. к. 2х2 − х − 3 = 2х2 − 4х + 3х − 6 + 3 =
= 2х(х − 2) + 3(х − 2) + 3 = (х − 2)(2х + 3) + 3,
Пример 2
+ 3
Деление многочленов с остатком
то 2х2 − х − 3 = (х − 2)(2х + 3) + 3
−

Теорема Безу
р(x) = (x − а) q(x) + r
Остаток от деления многочлена р(х) ненулевой степени на двучлен x − а равен р(а)
(т.е. значению многочлена р(x) при х = а)
p(x) – делимое (или кратное)
q(x) – частное
r – остаток (число)
x − а – делитель

По теореме Безу: р(2)= 2⋅22 − 2 − 3 = 3
2х2 − х − 3
х − 2
2х2 − 4х
−
3х − 6
2х
3х − 3
3
Найдем остаток от деления многочлена
р(х) = 2х2 − х − 3 на двучлен х − 2.
Пример 2
+ 3
Деление многочленов с остатком
−

Следствие теоремы Безу
Если число а является корнем многочлена р(х), то р(х) делится на двучлен x − а.
Если при х = а многочлен р(х) обращается в нуль, т.е. выполняется равенство р(а) = 0, то число а называют корнем многочлена.
Следствие
Определение

Схема Горнера
Пусть р(x) = bx4 + cx3 + dx2 + ex + f. Разделим р(х) на x − а получим р(x) = (х − а )q(x) + r, где q(x) некоторый многочлен третьей степени q(x) = kx3 + mx2 + nx + s, коэффициенты которого вычисляются с помощью схемы Горнера:
k = b
m = ka + c
n = ma + d
s = na + e
r = sa + f

Коэффициенты частного: 2, − 3, 3, − 4, 8,
а остаток r = − 11.
Значит, 2x5 + x4 − 3x3 + 2x2 + 5 =
= (х + 2)(2x4 − 3x3 + 3x2 − 4x + 8) − 11
Разделим р(x) = 2x5 + x4 − 3x3 + 2x2 + 5 на x + 2.
Здесь a = − 2; Коэффициенты равны соответственно
2, 1, −3, 2, 0, 5.
Строим таблицу для применения схемы Горнера:
Пример 3
−2
2
2
2⋅(−2)+1
−3
−3⋅(−2)+(−3)
3
3⋅(−2)+2
−4
−4⋅(−2)+0
8
8⋅(−2)+5
−11

Разложение многочлена на множители

Вынесение общего множителя за скобки
Применяя распределительный закон умножения относительно сложения:
(a + b)c = ac + bc
В обратном порядке:
ac + bc = c(a + b)
Пример 4
8х4 + 6х3 − 4х2 + 2х =
2х (4х3 + 3х2 − 2х + 1)
3х3 + 6х6 − 27х4 =
3x3 (1 + 2х3 − 9x)

Способ группировки
Применяя переместительный или сочетательный законы сложения, можно группировать члены многочлена любым способом:
a + b = b + a
(a + b) + c = a + (b + c) = а + b + c
Пример 5
3х3 + 6х2 − 27х − 54 =
3(х3 + 2х2 − 9х − 18) =
= 3(х2 (х + 2) − 9(х + 2)) =
3(х + 2)(х2 − 9) =
= 3(х + 2)(х − 3)(х + 3)

Использование формул
сокращенного умножения
(a + b)(а − b) = a2 − b2 – разность квадратов
(a + b)2 = a2 + 2ab + b2 – квадрат суммы
(a − b)2 = a2 − 2ab + b2 – квадрат разности
(a + b)(a2 − ab + b2) = а3 + b3 – сумма кубов
(a − b)(a2 + ab + b2) = а3 − b3 – разность кубов
(a − b)3 = a3 − 3ab2 + 3a2b − b3 – куб разности
(a + b)3 = a3 + 3ab2 + 3a2b + b3 – куб суммы
Пример 6
х6 − 1 =
= (х + 1)(х2 − х + 1)(х − 1)(х2 + х + 1)
(х3)2 − 12 = (х3 + 1)(х3 − 1) =

Разложение квадратного трехчлена
на линейные множители
Если х1 и х2 – корни квадратного трехчлена
aх2 + bх + с, то
aх2 + bх + с = а (х − х1)(х − х2)
Пример 7
2х2 − 3х − 5 =
2 (х + 1)(х − 2,5) =
(х + 1)(2х − 5)

Теорема
Пусть все коэффициенты многочлена р(х) – целые числа. Если целое число а является корнем многочлена р(х), то а – делитель свободного члена многочлена р(х).
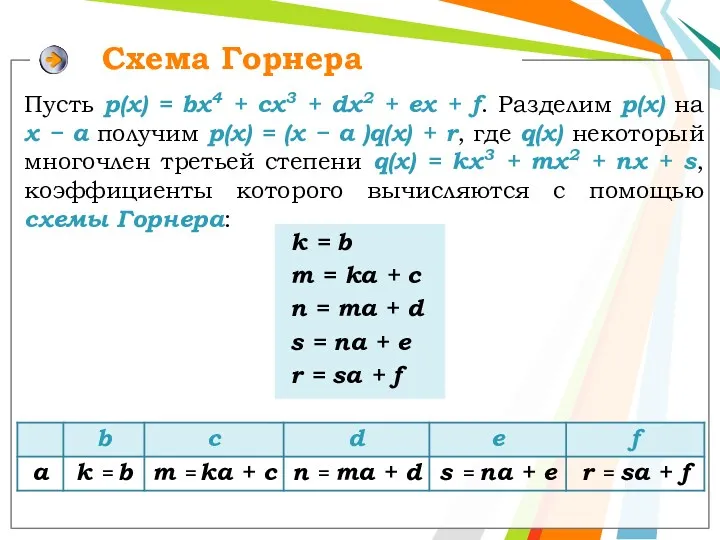
Д о к а з а т е л ь с т в о проведем для случая, когда р(х) – многочлен третьей степени: р(х) = bх3 + сх2+ dx + т, где все коэффициенты b, с, d, т – целые числа. По условию, целое число а является корнем многочлена р(х).
Это значит, что р(а) = 0, т. е. bаз + ca2 + da + m = 0.
Преобразуем полученное равенство к виду т = а(– bа2 – са – d) и обозначим целое число (– bа2 – са – d) буквой k.
Тогда последнее равенство можно переписать в виде т = ak, а это и означает, что число а – делитель числа т, т. е. делитель свободного члена многочлена р(х).
Аналогично проводится доказательство теоремы для случая, когда р(х) – многочлен четвертой, пятой и вообще n-й степени.

Пример 8
х3 − 3х2 − 10х + 24 =
(х – 2)(х2 − х − 12) =
= (х – 2)(х − 4)(х + 3)
Разложить многочлен: х3 − 3х2 − 10х + 24
Будем искать корни среди делителей свободного коэффициента 24: ± 1; ± 2; ± 3; ± 4; ± 6; ± 8; ± 12; ± 24.
р(1) = 12 ≠ 0, р(−1) = 30 ≠ 0, р(2) = 0.
Значит х = 2 – корень многочлена р(х). С помощью схемы Горнера найдем частное q(x):
2
1
1
2⋅1+(−3)
−1
2⋅(−1)−10
−12
2⋅(−12)+24
0

х2 – у2 = (х – у)(х + у)
х3 – у3 = (х – у)(х2 + ху + у2)
x4 – у4 = (x – y)(x3 + x2у + xy2 + уЗ)
x5 – у5 = (x – y)(х4 + хзy + х2y2 + хy3 + y4)
…
xn – уn = (x – y)(хn−1 + хn−2y + хn−3y2 + … +
+ х2yn−3 + xyn−2 + yn−1)
Многочлены от нескольких переменных

Многочлены от нескольких переменных
х3 + у3 = (х + у)(х2 – ху + у2)
x5 + у5 = (x + y)(х4 – х3y + х2y2 – хy3 + y4)
…
x2n+1 + у2n+1 = (x + y)(х2n – х2n−1y + х2n−2y2 –
– х2n−3y3 + … + x2y2n−2 – xy2n−1 + y2n)
Многочлен Р(х; у) называют однородным многочленом п-ой степени, если сумма показателей степеней переменных в каждом члене многочлена равна п.
Если Р(х; у) однородный многочлен, то уравнение Р(х; у) = 0 называют однородным уравнением.