Содержание
- 2. ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ Задана система вузлів та значень функції у вузлах : Поліном називається узагальненим поліномом, де
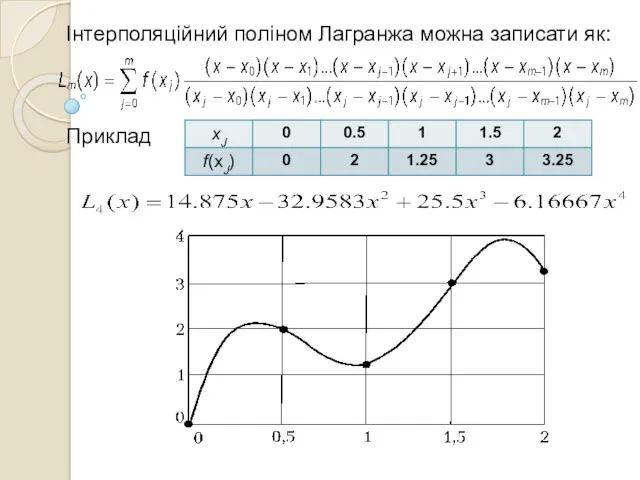
- 5. НАБЛИЖЕННЯ ФУНКЦІЙ Інтерполяційний поліном Лагранжа можна записати як: де – поліном степеня m, що у вузлах
- 7. Інтерполяційний поліном Лагранжа можна записати як: Приклад .
- 8. ПОХИБКИ ФОРМУЛИ ЛАГРАНЖА Різницю між функцією та її інтерполяційним наближенням називають залишковим членом інтерполяційної формули або
- 9. y = ln x x0 = 1.1; x1= 1.2; x0 = 1.1; x1= 1.2; x2= 1.3;
- 11. Скінченні різниці першого порядку: Скінченні різниці другого порядку: У загальному випадку скінченні різниці k-го порядку: .
- 12. . ВЛАСТИВОСТІ СКІНЧЕННИХ РІЗНИЦЬ Скінченні різниці сталої дорівнюють нулю. Сталий множник можна виносити за знак скінченної
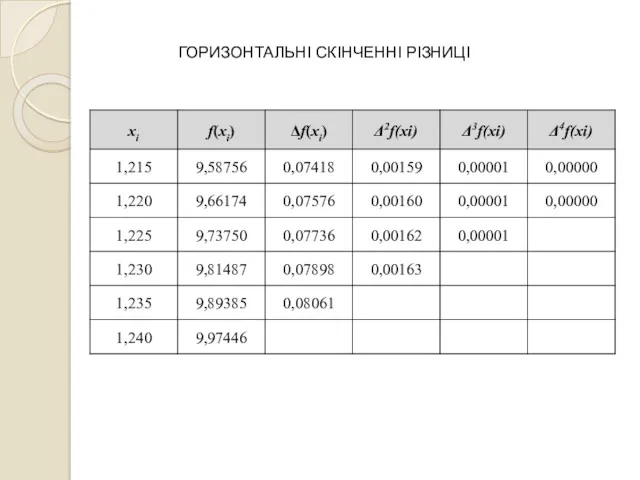
- 13. ГОРИЗОНТАЛЬНІ СКІНЧЕННІ РІЗНИЦІ
- 14. ГОРИЗОНТАЛЬНІ СКІНЧЕННІ РІЗНИЦІ
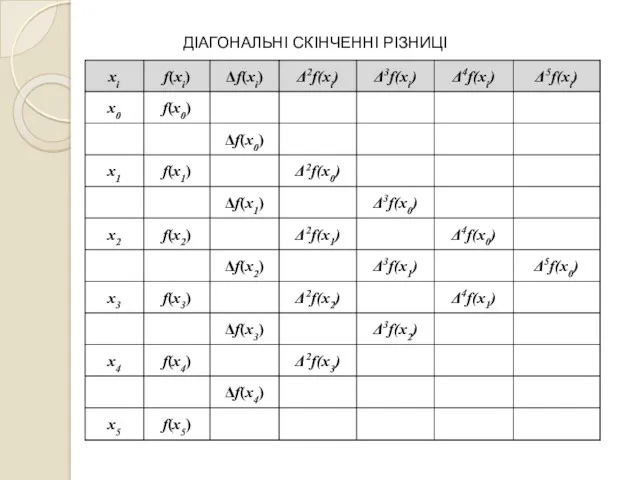
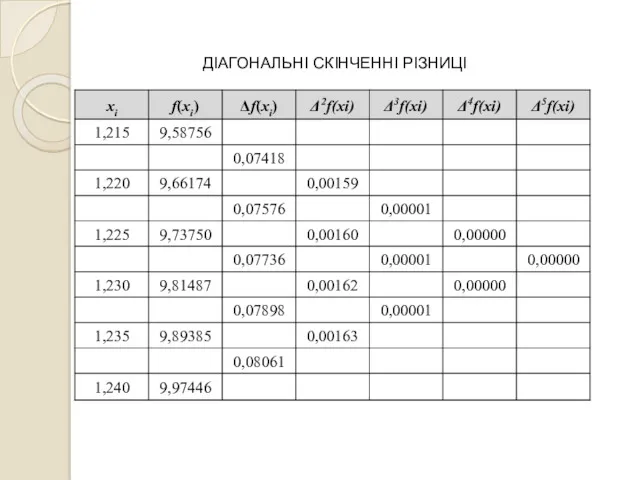
- 15. ДІАГОНАЛЬНІ СКІНЧЕННІ РІЗНИЦІ
- 16. ДІАГОНАЛЬНІ СКІНЧЕННІ РІЗНИЦІ
- 17. ПЕРША ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА Нехай, вузли інтерполяції розташовані рівномірно: Побудуємо інтерполяційний поліном у вигляді: Задача полягає
- 20. ДРУГА ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА Нехай, вузли інтерполяції розташовані рівномірно: Побудуємо інтерполяційний поліном у вигляді: Задача полягає
- 24. ВИБІР ВУЗЛІВ ІНТЕРПОЛЯЦІЇ Похибки інтерполяційних формул дорівнюють добутку двох множників, з яких один, залежить від властивостей
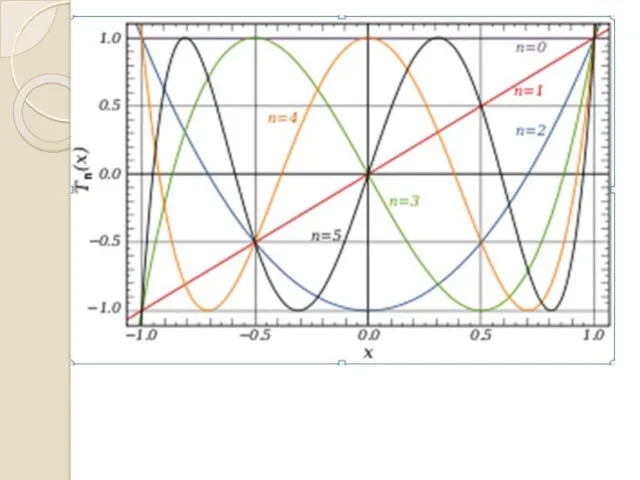
- 27. Поліноми Чебишева першого роду можуть бути визначені за допомогою рекурсивних співвідношень (n>=2) :
- 29. ЗБІЖНІСТЬ ІНТЕРПОЛЯЦІЙНОГО ПРОЦЕСУ Збільшення кількості вузлів інтерполяції з метою зменшення похибки не завжди виправдане. Необхідно досліджувати
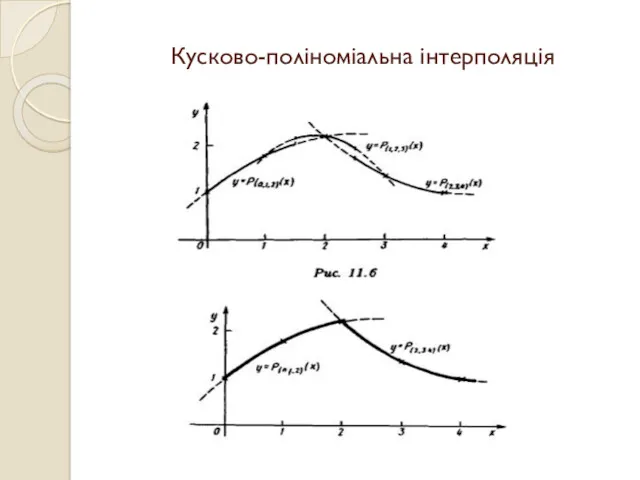
- 30. Кусково-поліноміальна інтерполяція
- 31. СПЛАЙНИ Поліном третього степеня називається кубічним сплайном що відповідає функції і заданий на сітці вузлів якщо
- 32. СЛАР для обчислення коефіцієнтів сплайна: СЛАР з (4m – 4) рівнянь має (4m – 4) невідомих
- 33. Дану СЛАР після перетворень можна звести до СЛАР з тридіагональною матрицею виду:
- 34. Теорема. Нехай функція f(x)∈ C4[a,b]. Тоді для кубічного сплайну S(x), побудованого на системі вузлів справедливі нерівності:
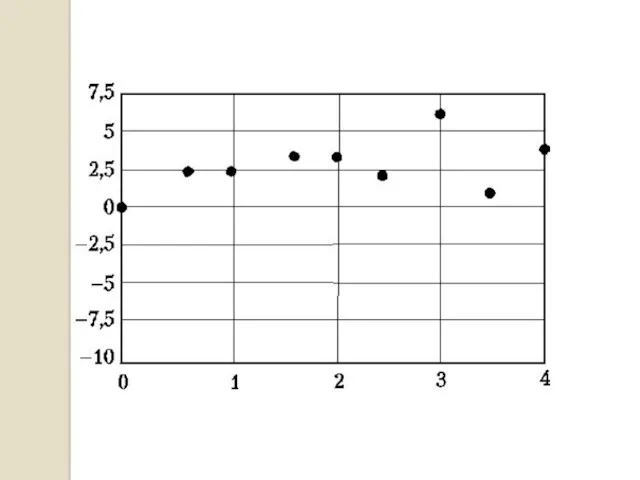
- 36. {xi,f(xi)} = {(0, 0), (0.5, 2), (1., 2.25), (1.5, 3), (2,3.25), (2.5, 3), (3, 6), (3.5,
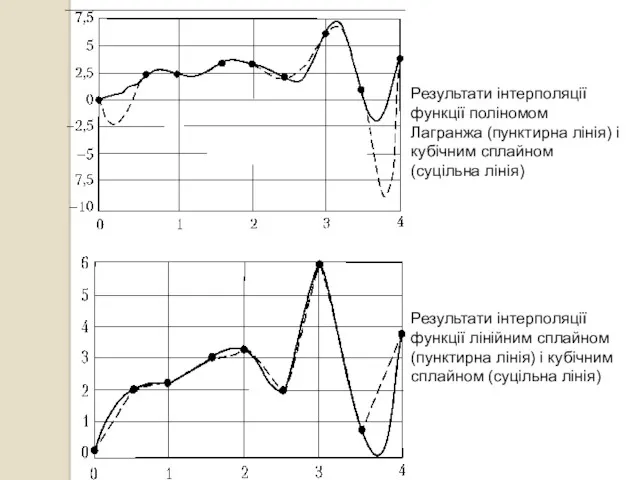
- 37. Результати інтерполяції функції лінійним сплайном (пунктирна лінія) і кубічним сплайном (суцільна лінія) Результати інтерполяції функції поліномом
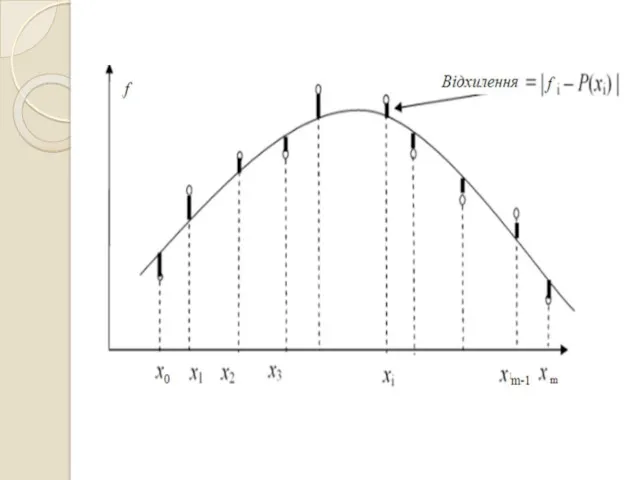
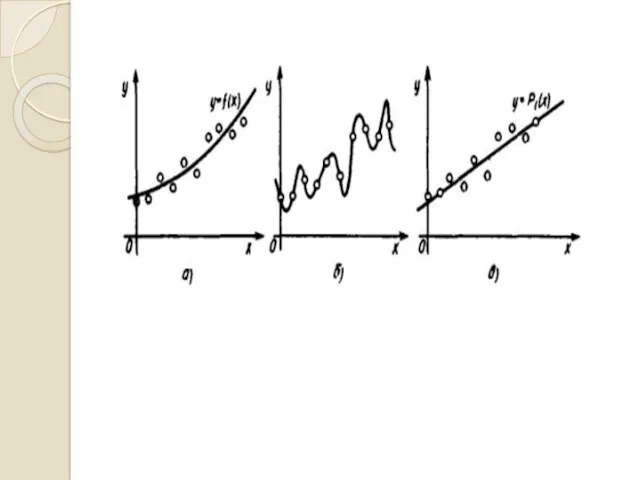
- 38. МЕТОД НАЙМЕНШИХ КВАДРАТІВ Міра відхилення заданих значень від обраної функції у заданих точках повинна бути мінімальною.
- 40. Необхідно, щоб для всіх коефіцієнтів виконувалась умова: Почнемо з Далі продовжимо для всіх
- 41. У результаті отримуємо СЛАР виду:
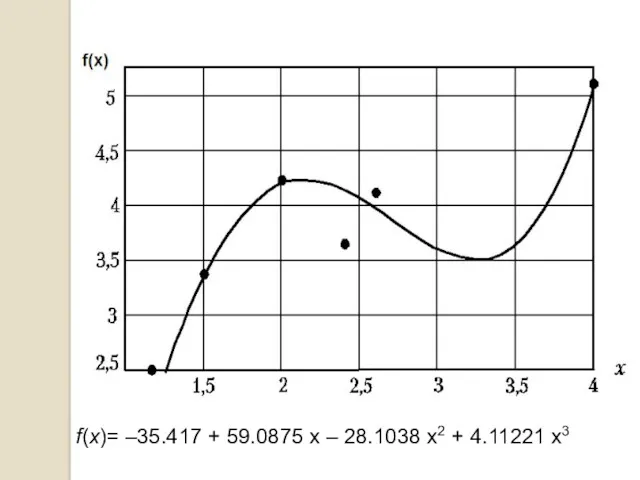
- 46. f(x)= –35.417 + 59.0875 x – 28.1038 x2 + 4.11221 x3
- 48. Скачать презентацию

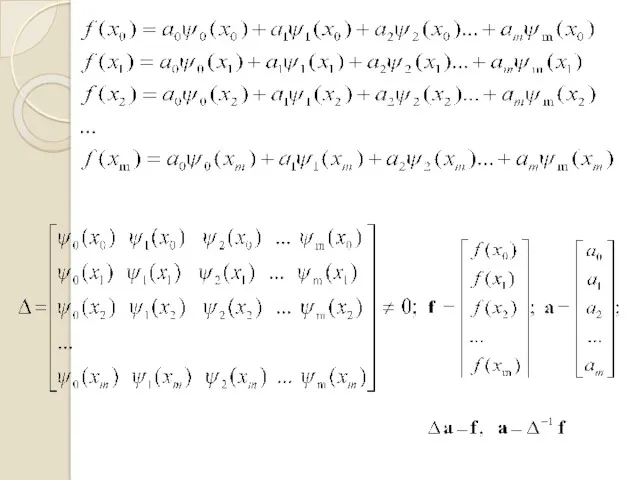





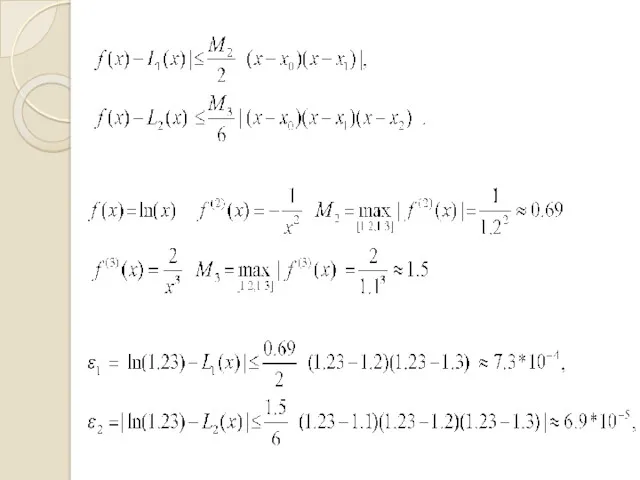









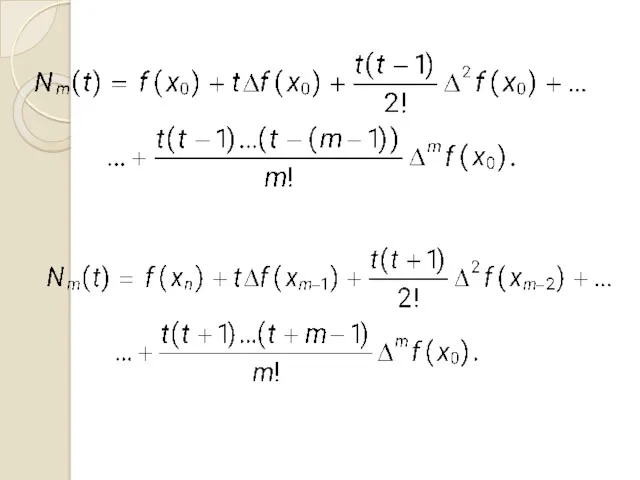

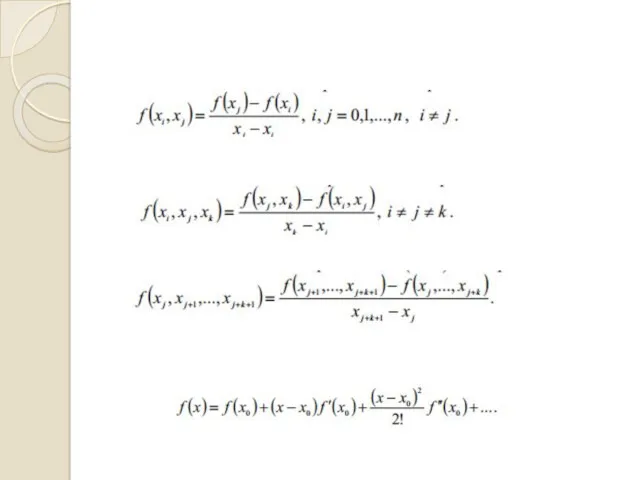






![Теорема. Нехай функція f(x)∈ C4[a,b]. Тоді для кубічного сплайну S(x),](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/141923/slide-33.jpg)




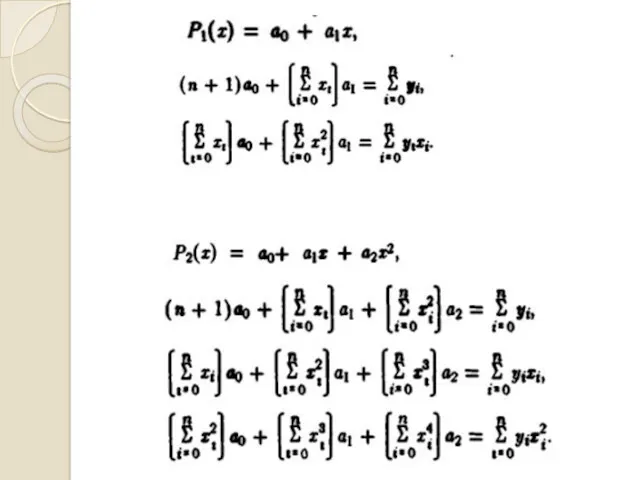

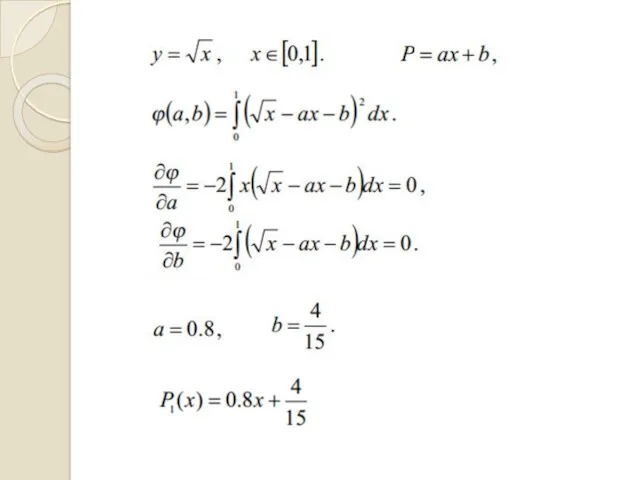
 Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Урок математики в 3 классе по теме: Знакомство с соотношениям Презентация к уроку Знакомство с соотношениями между ценой, количеством и стоимостью.
Урок математики в 3 классе по теме: Знакомство с соотношениям Презентация к уроку Знакомство с соотношениями между ценой, количеством и стоимостью. Числовые функции. Понятие функции
Числовые функции. Понятие функции Двугранный угол
Двугранный угол презентация задачи в стихах (два действия)
презентация задачи в стихах (два действия) Сфера и шар. 10 класс
Сфера и шар. 10 класс Основы векторной алгебры. Векторы на плоскости и в пространстве
Основы векторной алгебры. Векторы на плоскости и в пространстве Исследование функций. Чтение графика
Исследование функций. Чтение графика Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Авторское учебно-методическое пособие Счёт до 5
Авторское учебно-методическое пособие Счёт до 5 Перпендикулярність площин
Перпендикулярність площин Упрощение выражений. Решение уравнений
Упрощение выражений. Решение уравнений История развития тригонометрии
История развития тригонометрии Следствия из аксиом стереометрии
Следствия из аксиом стереометрии Тест по математике 4 класс Диск
Тест по математике 4 класс Диск Десятичная запись дробных чисел (повторение)
Десятичная запись дробных чисел (повторение) Основы статистики. Статистика & Биостатистика
Основы статистики. Статистика & Биостатистика Урок математики 2класс
Урок математики 2класс Стереометрия. Расстояния в пространстве. Задания В 9, ЕГЭ
Стереометрия. Расстояния в пространстве. Задания В 9, ЕГЭ Окружность и круг
Окружность и круг Параллелепипеды. Прямоугольные параллелепипеды. Куб
Параллелепипеды. Прямоугольные параллелепипеды. Куб Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка
Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Гипотезы, переменные, валидность, данные. Введение в статистику, лекция 1
Гипотезы, переменные, валидность, данные. Введение в статистику, лекция 1 Функции и графики
Функции и графики Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ
Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ Признаки параллельности прямых (7 класс)
Признаки параллельности прямых (7 класс) Статистика и теория вероятностей. Подготовка к решению задач на ОГЭ и ЕГЭ
Статистика и теория вероятностей. Подготовка к решению задач на ОГЭ и ЕГЭ