Содержание
- 2. КОНФУЦИЙ – древнекитайский философ и мыслитель «Три пути ведут к знанию: путь размышления – это путь
- 3. Цели урока : Обобщить и закрепить понятие неопределённого интеграла. Повторить основные свойства интеграла. Отработать практические навыки
- 4. Организационный этап. Из истории неопределённого интеграла. Фронтальный опрос по теории. Работа по карточкам. Математическая эстафета. Закрепление
- 5. ИСТОРИЯ ВОЗНИКНОВЕНИЯ ИНТЕГРАЛА
- 6. Определение Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции
- 7. Символ интеграла был введён Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы
- 8. Интеграл в древности Возникновение задач интегрального исчисления связано с нахождением площадей и объемов. Ряд задач такого
- 9. Интеграл в древности Однако Архимед не выделил общего содержания интеграционных приемов и понятий об интеграле, а
- 10. История возникновения интеграла Труды Архимеда, впервые изданные в 1544 (на латинском и греческом языках), стали привлекать
- 11. История возникновения интеграла Например, криволинейную трапецию они представляли себе составленной из вертикальных отрезков длиной f(x) ,
- 12. История возникновения интеграла На такой кажущейся теперь по меньшей мере сомнительной основе И. Кеплер (1571 -
- 13. История возникновения интеграла В XVII веке были сделаны многие открытия, относящиеся к интегральному исчислению. Однако при
- 14. История возникновения интеграла Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам
- 15. История возникновения интеграла Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и
- 16. История возникновения интеграла Методы математического анализа активно развивались в следующем столетии (в первую очередь следует назвать
- 17. История возникновения интеграла Строгое изложение теории интеграла появилось только в прошлом веке, Решение этой задачи связано
- 18. История возникновения интеграла Ответы на многие вопросы, связанные с существованием площадей и объемов фигур, были получены
- 19. История возникновения интеграла Различные обобщения понятия интеграла уже в начале нашего столетия были предложены французскими математиками
- 20. Фронтальный опрос по теории Вопросы 1. Дать определение неопределённого интеграла. 2. Какие способы вычисления неопределённого интеграла
- 21. Вопросы для повторения Вопросы 3. Что называется интегрированием? 4. Чем отличаются друг от друга различные первообразные
- 22. Вопросы для повторения Вопросы 5. Какая функция называется первообразной для данной функции f(x)?
- 23. Вопросы для повторения Вопросы 6. Сформулируйте свойства неопределённого интеграла…
- 24. Таблица неопределенных интегралов
- 25. Таблица неопределенных интегралов
- 26. МАТЕМАТИЧЕСКАЯ ЭСТАФЕТА Инструктаж: Работа в командах (по рядам). На последней парте каждого ряда находится листок с
- 27. Закрепление практических умений и навыков Решение типовых примеров по образцу
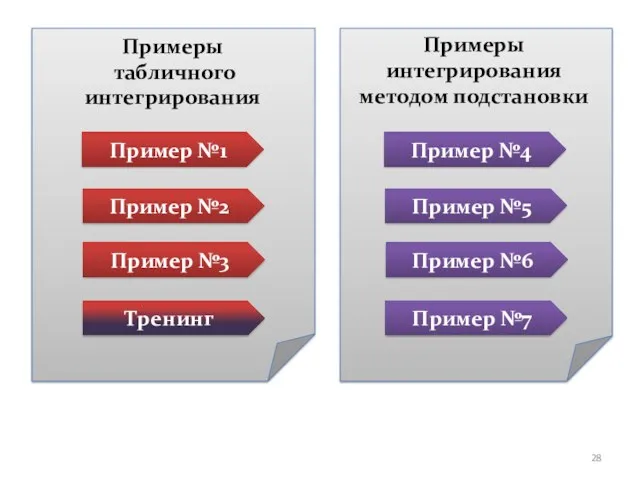
- 28. Примеры табличного интегрирования Примеры интегрирования методом подстановки Пример №1 Пример №2 Пример №3 Тренинг Пример №4
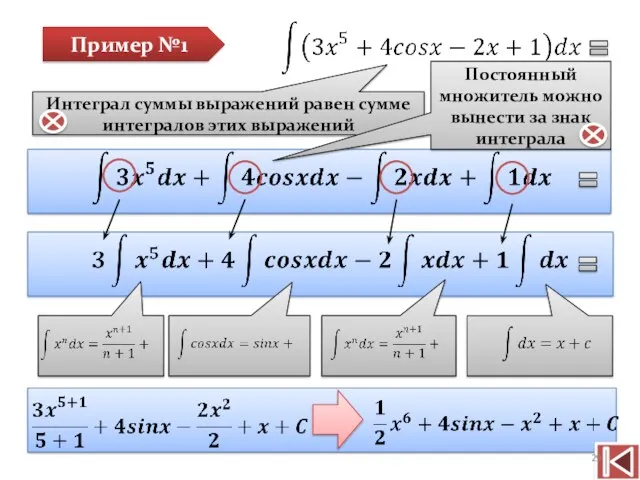
- 29. Пример №1 Интеграл суммы выражений равен сумме интегралов этих выражений Постоянный множитель можно вынести за знак
- 30. Пример №2 Записать решение: Проверить решение ?
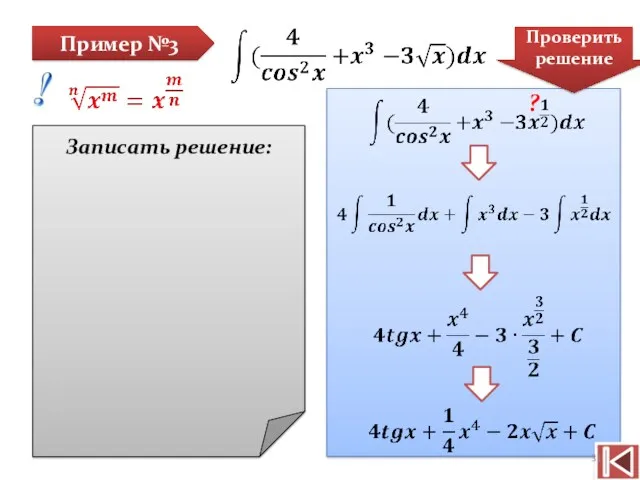
- 31. Пример №3 Записать решение: Проверить решение ?
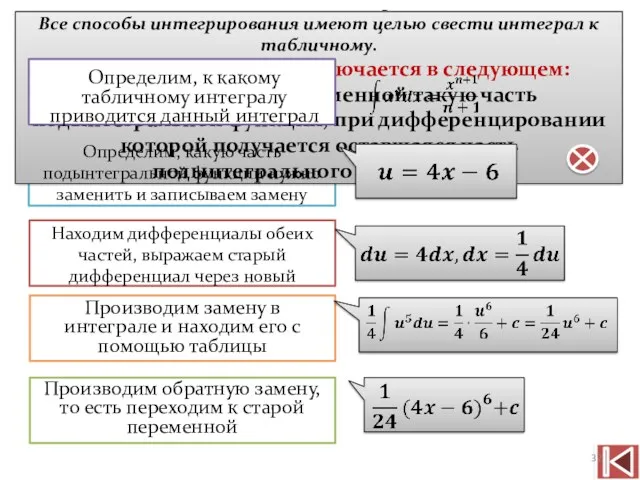
- 32. Пример №4 Все способы интегрирования имеют целью свести интеграл к табличному. Способ подстановки заключается в следующем:
- 33. Введем новую переменную и выразим дифференциалы: Пример №5 Записать решение: Проверить решение
- 34. Введем новую переменную и найдем её дифференциал Пример №6 Записать решение: Проверить решение
- 35. Пример №7 Записать решение: Проверить решение
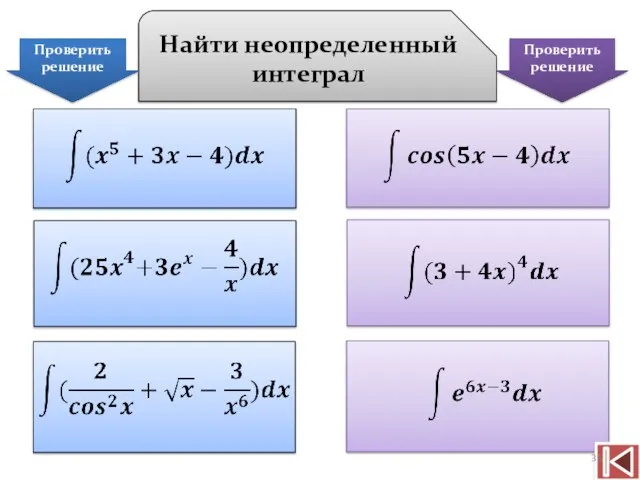
- 36. Найти неопределенный интеграл Проверить решение Проверить решение
- 37. Следует отметить, что для функции вида f(kx+b) можно применять упрощенную формулу
- 38. Решение типичных примеров 1. Вычислить интеграл: 2. Вычислить интеграл методом подстановки: 3. Вычислить интеграл методом интегрирования
- 39. 1 пример
- 40. 2 пример
- 41. 3 пример
- 42. Применение практических умений и навыков «ВЫПОЛНЕНИЕ ПРАКТИЧЕСКОЙ РАБОТЫ»
- 43. ПРОВЕРКА УМЕНИЙ и НАВЫКОВ Самостоятельная работа по теме: «Вычисление неопределённого интеграла» КРИТЕРИЙ ОЦЕНОК: ОЦЕНКА «5» –
- 44. Информация по домашнему заданию: Повторить основные понятия и свойства по теме «Неопределённый интеграл». Составить кроссворд (ребус)
- 46. Скачать презентацию
































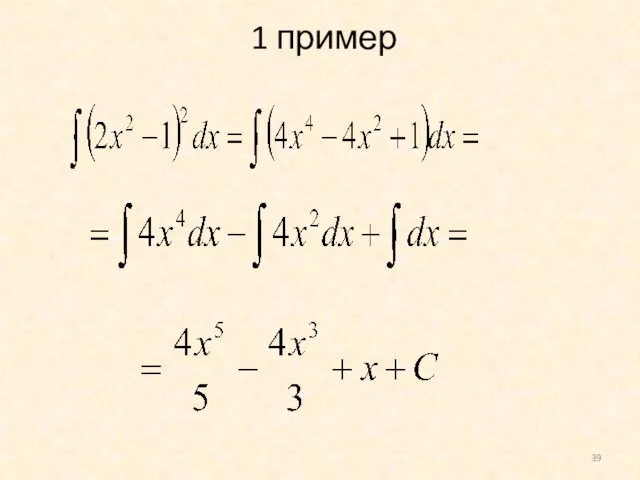
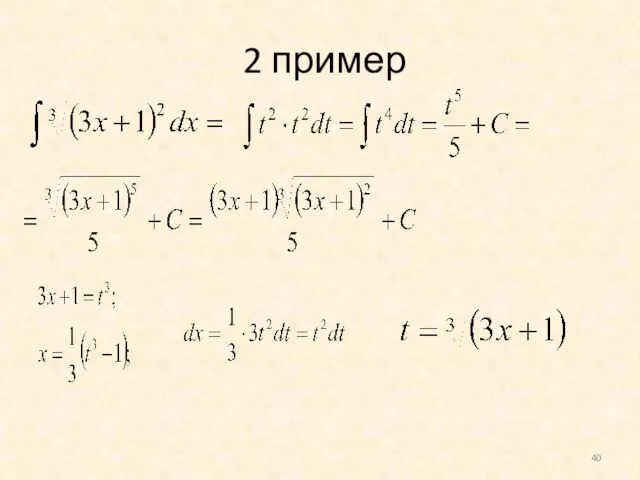
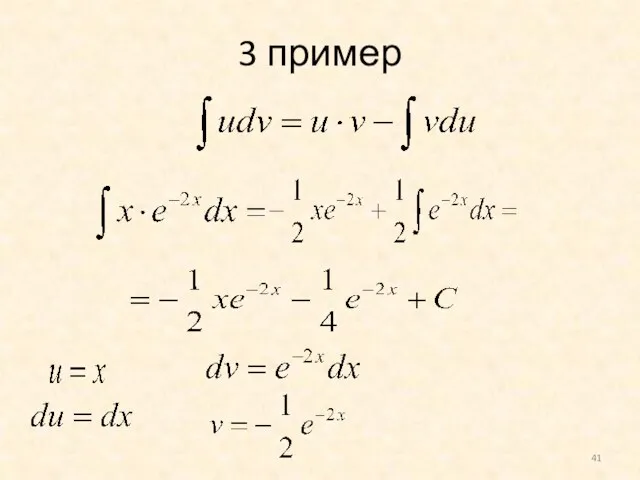



 Золотое сечение
Золотое сечение Урок математики в 1 классе Вспоминаем, повторяем
Урок математики в 1 классе Вспоминаем, повторяем Теорема: средняя линия треугольника
Теорема: средняя линия треугольника Аналитическая геометрия на плоскости
Аналитическая геометрия на плоскости 20190222_5_klass_desyatichnaya_zapis_drobnyh_chisel
20190222_5_klass_desyatichnaya_zapis_drobnyh_chisel Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация)
Влияние поисково-исследовательской деятельности на развитие логико-конструктивного мышления и формирование математических способностей дошкольников (презентация) Математический тренажер 4 класс
Математический тренажер 4 класс Таблица умножения на 4
Таблица умножения на 4 Последовательность. Выборки из множеств, сходимость. Свойства пределов последовательностей и сходящихся последовательностей
Последовательность. Выборки из множеств, сходимость. Свойства пределов последовательностей и сходящихся последовательностей Натуральные числа. Математика, 5 класс
Натуральные числа. Математика, 5 класс Определение прямоугольного треугольника. Теорема Пифагора
Определение прямоугольного треугольника. Теорема Пифагора Алгебра логики
Алгебра логики Что узнали и чему научились в 1 классе
Что узнали и чему научились в 1 классе Множественная линейная регрессия
Множественная линейная регрессия Стохастические модели приземных трасс
Стохастические модели приземных трасс презентация к конспекту по математике Прибавление числа 5
презентация к конспекту по математике Прибавление числа 5 Урок математики Умножение и деление на 10 и на 100. Символы олимпиады Сочи 2014
Урок математики Умножение и деление на 10 и на 100. Символы олимпиады Сочи 2014 Тема. Деление на круглое число.
Тема. Деление на круглое число. Вывести правило вычитания рациональных чисел и сформулировать алгоритм
Вывести правило вычитания рациональных чисел и сформулировать алгоритм Прямая пропорциональность. Устная работа
Прямая пропорциональность. Устная работа уроки математики УМК Школа России
уроки математики УМК Школа России Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Динамика полета. Разгон и торможение самолета. (Лекция 7)
Динамика полета. Разгон и торможение самолета. (Лекция 7) Компоненты действия деления
Компоненты действия деления Параллелограмм
Параллелограмм урок математики в 4 классе УМК Школа России Тема Деление многозначных чисел на однозначные. закрепление.
урок математики в 4 классе УМК Школа России Тема Деление многозначных чисел на однозначные. закрепление. ГИА - 2016. Открытый банк заданий по математике. Задача №2
ГИА - 2016. Открытый банк заданий по математике. Задача №2 Умножение круглых сотен. 3 класс
Умножение круглых сотен. 3 класс