Слайд 2

План:
1. Плотность распределения и ее свойства.
2. Числовые характеристики НСВ.
Слайд 3

1. Плотность распределения и ее свойства
Плотностью распределения вероятностей или плотностью
распределения f (x) непрерывной случайной величины X называется производная ее функции распределения F (x)
Слайд 4
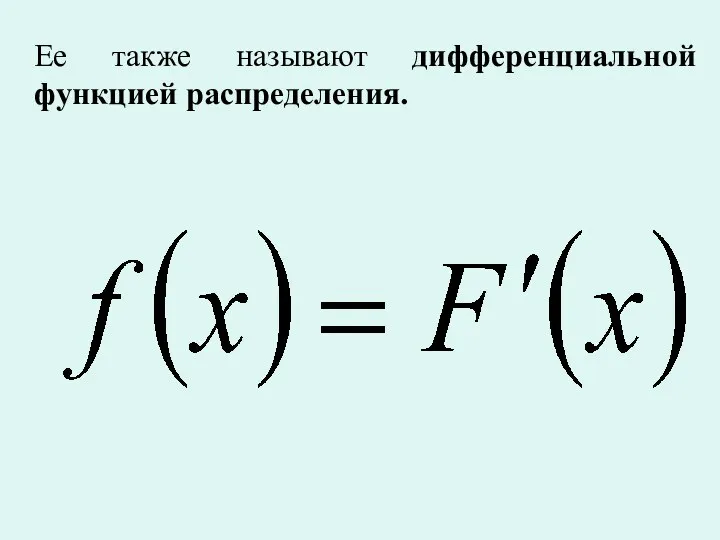
Ее также называют дифференциальной функцией распределения.
Слайд 5

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее
интервалу (a ; b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:
Слайд 6
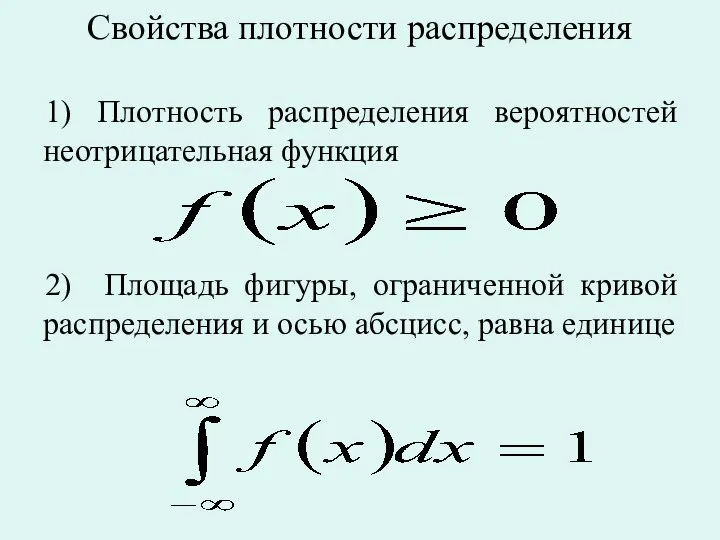
Свойства плотности распределения
1) Плотность распределения вероятностей неотрицательная функция
2) Площадь фигуры, ограниченной
кривой распределения и осью абсцисс, равна единице
Слайд 7

2. Числовые характеристики НСВ
Математическим ожиданием непрерывной случайной величины X, возможные значения
которой принадлежат отрезку от a до b, называют определенный интеграл:
Слайд 8
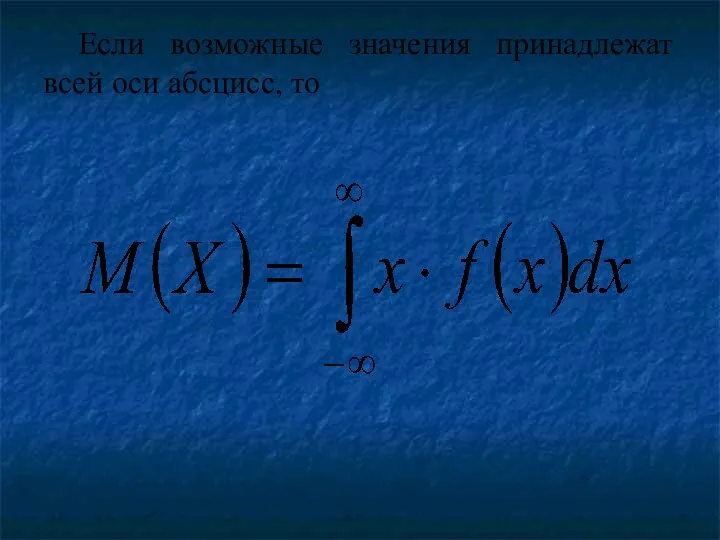
Если возможные значения принадлежат всей оси абсцисс, то
Слайд 9

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Слайд 10

Если возможные значения принадлежат отрезку , то
Слайд 11
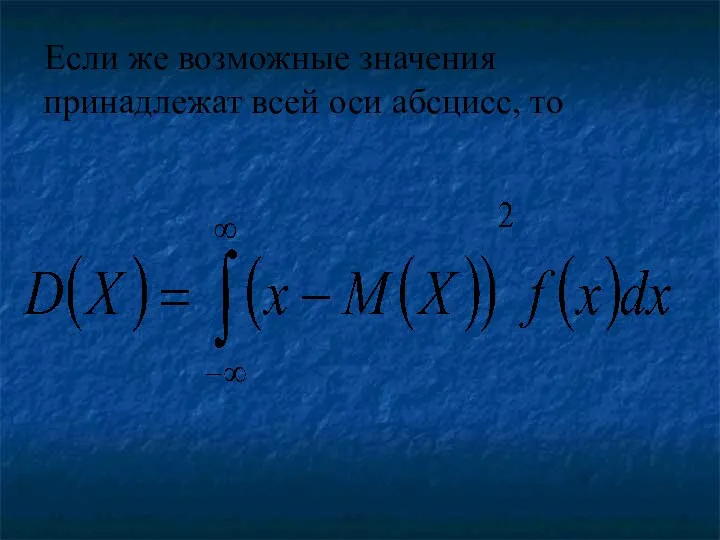
Если же возможные значения принадлежат всей оси абсцисс, то
Слайд 12

Среднее квадратическое отклонение непрерывной случайной величины определяется равенством
Слайд 13

Замечание 1.
Свойства математического ожидания и дисперсии дискретных случайных величин сохраняются
и для непрерывных величин.
Слайд 14

Замечание 2.
Для вычисления дисперсии НСВ X можно использовать более удобные
формулы:
Слайд 15

Пример. Найти плотность распределения и числовые характеристики случайной величины X заданной
интегральной функцией распределения
Слайд 16
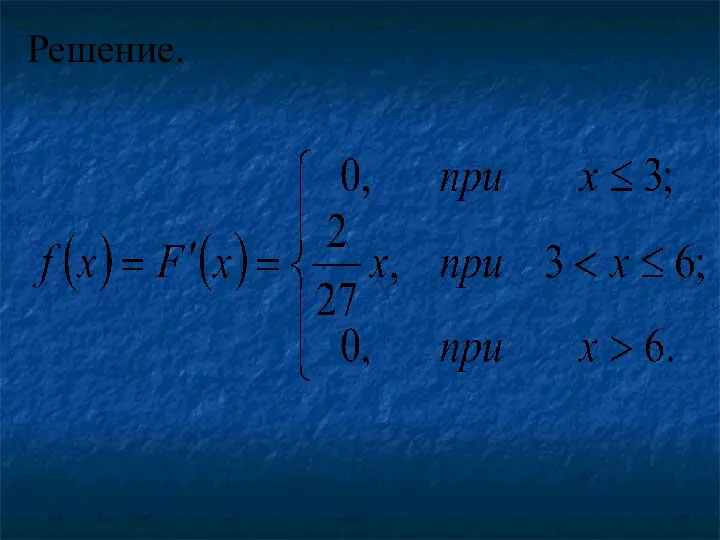
Слайд 17
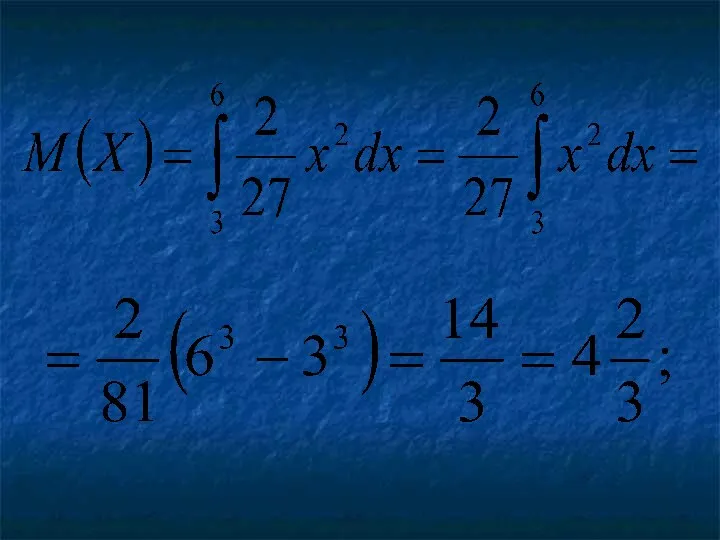
Слайд 18
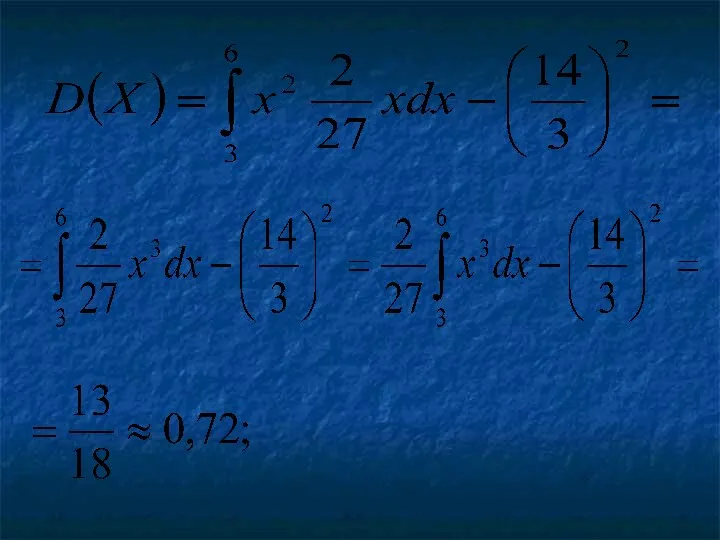
Слайд 19
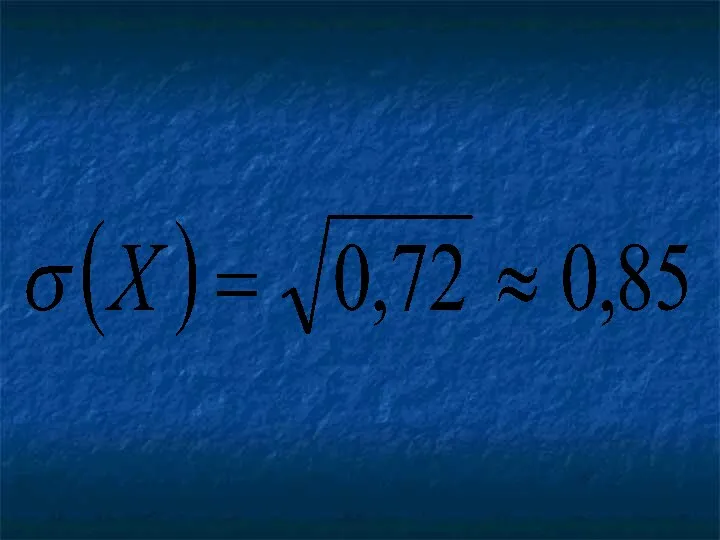
Слайд 20

Тема. Основные законы распределения НСВ
План:
Равномерный закон распределения.
Показательный закон распределения.
Нормальный закон распределения.
Слайд 21

При решении задач, которые выдвигает практика, приходится сталкиваться с различными распределениями
непрерывных случайных величин.
Слайд 22

Плотности распределений непрерывных случайных величин называют также законами распределений.
Часто встречаются
законы равномерного, нормального и показательного распределений.
Слайд 23

1. Равномерный закон распределения
Распределение вероятностей называют равномерным, если на интервале, которому
принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Слайд 24

НСВ считается равномерно распределенной, если ее плотность вероятности имеет вид
Слайд 25
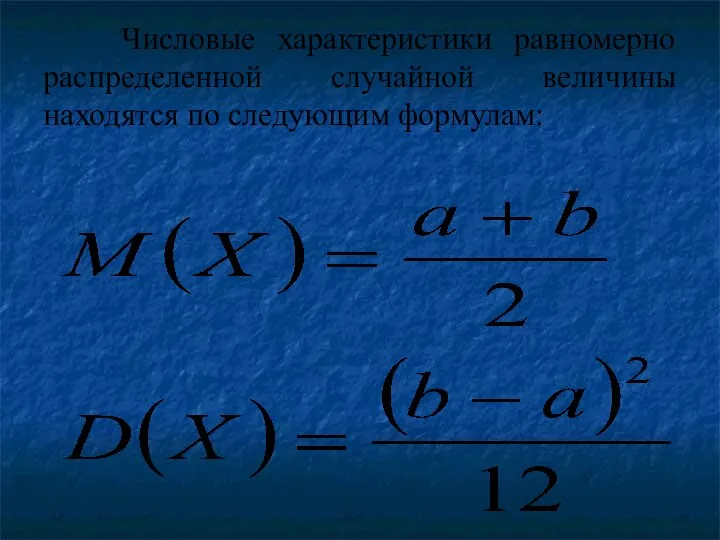
Числовые характеристики равномерно распределенной случайной величины находятся по следующим формулам:
Слайд 26

Пример. Случайная величина распределена равномерно в интервале (2;8). Найти ее математическое
ожидание и дисперсию.
Решение.
Слайд 27

2. Показательный закон распределения
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
X, которое описывается плотностью
где - постоянная положительная величина.
Слайд 28

Показательное распределение определяется одним параметром .
Эта особенность показательного распределения указывает
на его преимущество по сравнению с распределениями, зависящими от большего числа параметров.
Слайд 29

Найдем функцию распределения показательного закона:
Итак,
Слайд 30

Функция распределения показательного закона имеет вид:
Слайд 31

Графики функций F (x) и f (x)
0
1
0
1
Слайд 32

Вероятность попадания в заданный интервал показательно распределенной случайной величины
Вероятность попадания
в интервал непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения
вычисляется по формуле
Слайд 33

Пример. Непрерывная случайная величина X распределена по показательному закону
при
;
при .
Найти вероятность того, что в результате испытания X попадет в интервал (0,3 ;1).
Решение. По условию, .
Слайд 34

Числовые характеристики показательного распределения
Числовые характеристики непрерывной случайной величины X распределенной
по показательному закону вычисляются по формулам:
Слайд 35

Пример. Непрерывная случайная величина X распределена по показательному закону
при ;
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Слайд 36

Пример. Непрерывная случайная величина X распределена по показательному закону
при ;
при .
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Решение. По условию, . Следовательно,
Слайд 37

3. Нормальный закон распределения
Нормальным называют распределение вероятностей непрерывной случайной величины, которое
описывается плотностью
Слайд 38

Нормальное распределение определяется двумя параметрами:
Достаточно знать эти параметры, чтобы задать
нормальное распределение.
Слайд 39

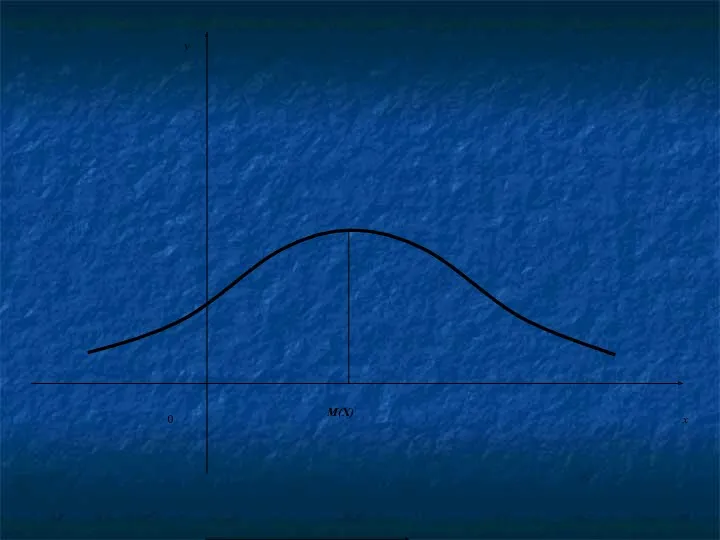
Нормальная кривая
График плотности нормального распределения называют нормальной кривой (кривой Гаусса).
Слайд 40
Слайд 41

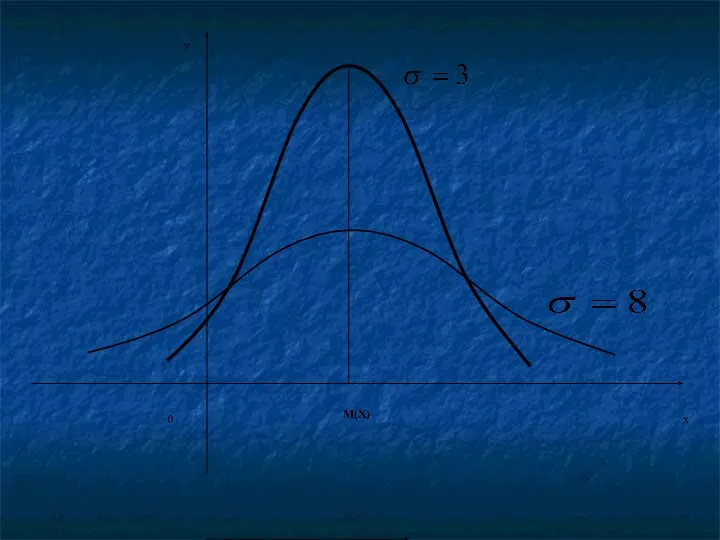
Влияние параметров нормального распределения на форму нормальной кривой.
Изменение величины параметра
не
изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси абсцисс: вправо, если математическое ожидание возрастает и влево, если оно убывает.
Слайд 42

С возрастанием среднего квадратического отклонения максимальная ордината нормальной кривой убывает, а
сама кривая становится более пологой, т.е. сжимается к оси абсцисс.
Слайд 43

При убывании среднего квадратического отклонения нормальная кривая становится более «островершинной» и
растягивается в положительном направлении оси ординат.
Слайд 44
Слайд 45

При математическом ожидании равном нулю и среднем квадратическом отклонении равном единице
нормальную кривую называют нормированной.
Слайд 46

Вероятность попадания в заданный интервал нормальной случайной величины
Пусть случайная величина распределена
по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна
Слайд 47

Вероятность попадания в заданный интервал нормальной случайной величины
Пусть случайная величина распределена
по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу , равна
Слайд 48

В результате преобразований и использования функции Лапласа
Слайд 49

Слайд 50

Пример. Случайная величина X распределена по нормальному закону с математическим ожиданием
равным 40 и средним квадратическим отклонением 30 . Найти вероятность того, что X примет значение, принадлежащее интервалу (20;70).
Слайд 51
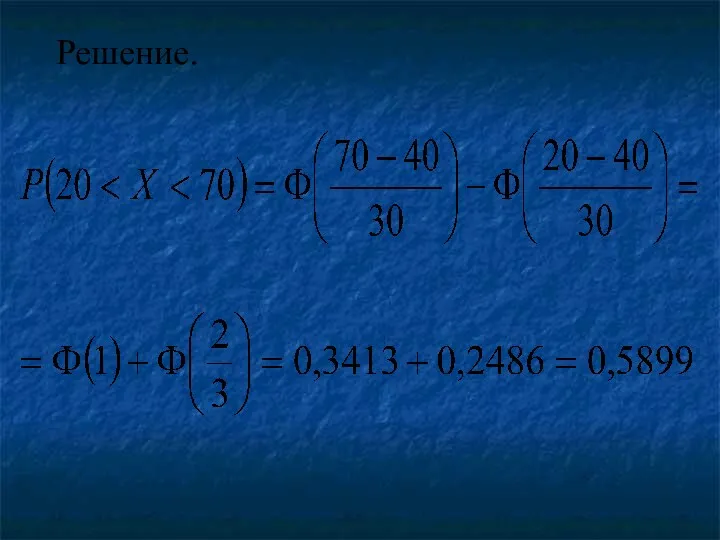
Слайд 52

Вычисление вероятности заданного отклонения
Часто требуется вычислить вероятность того, что отклонение нормально
распределенной случайной величины по абсолютной величине меньше заданного положительного числа , т. е. найти вероятность осуществления неравенства
Слайд 53
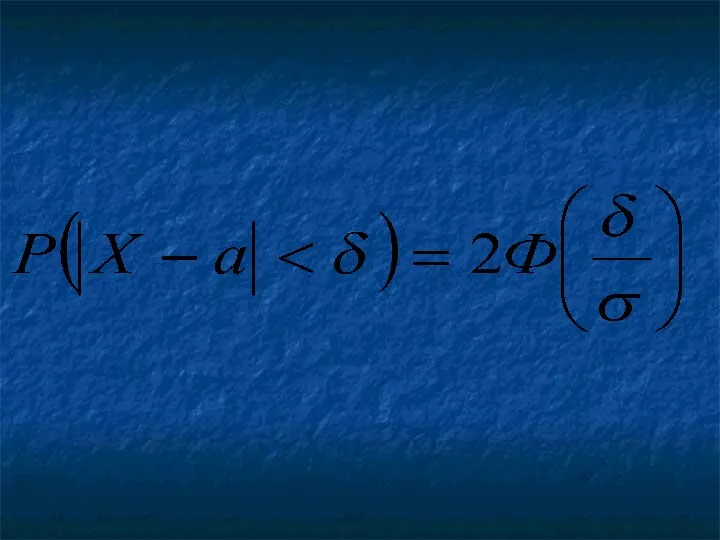
Слайд 54

Пример. Случайная величина распределена нормально
Найти вероятность того, что отклонение по
абсолютной величине будет меньше трех.
Слайд 55

Решение. Используя формулу
и данные условия задачи:
а также используя таблицу значений
функции Лапласа, получим:
Слайд 56
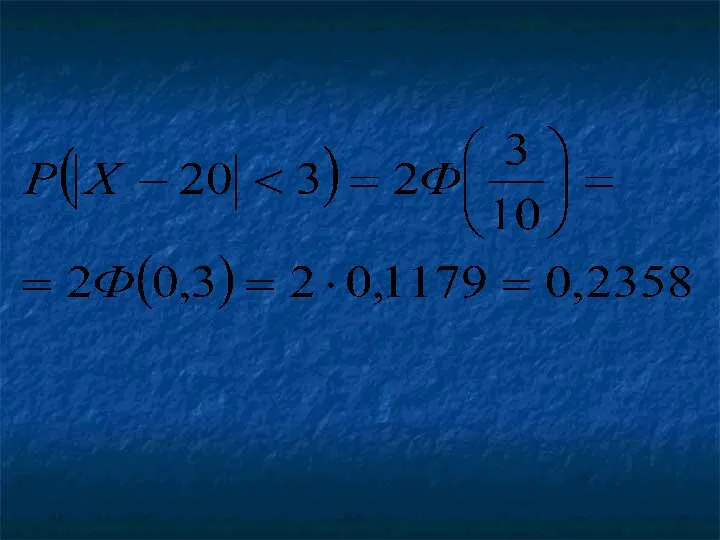
Слайд 57

Правило трех сигм
Правило трех сигм: Если случайная величина имеет нормальный
закон распределения с параметрами
то практически достоверно (вероятность 0,9973), что ее значения заключены в интервале


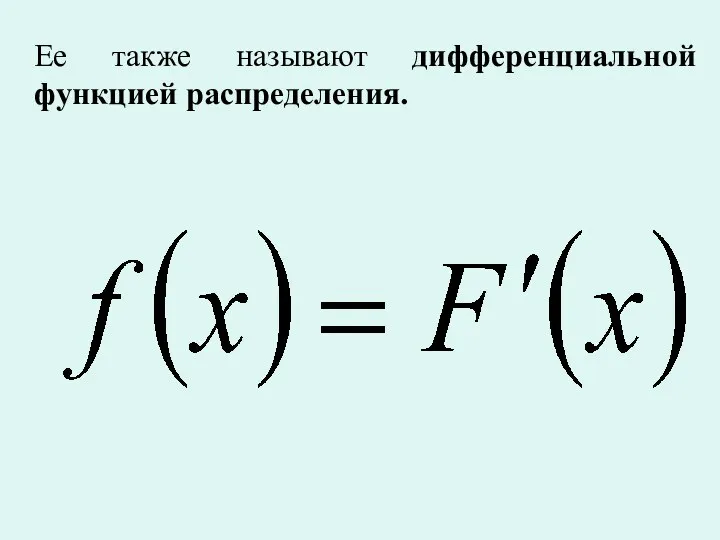

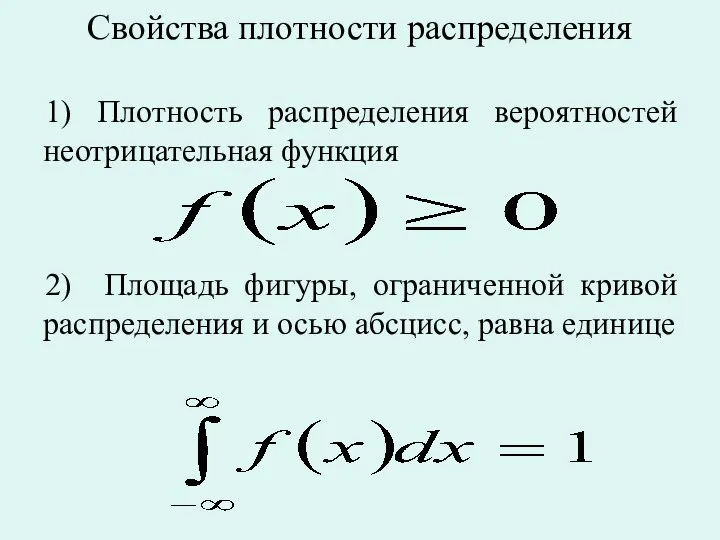

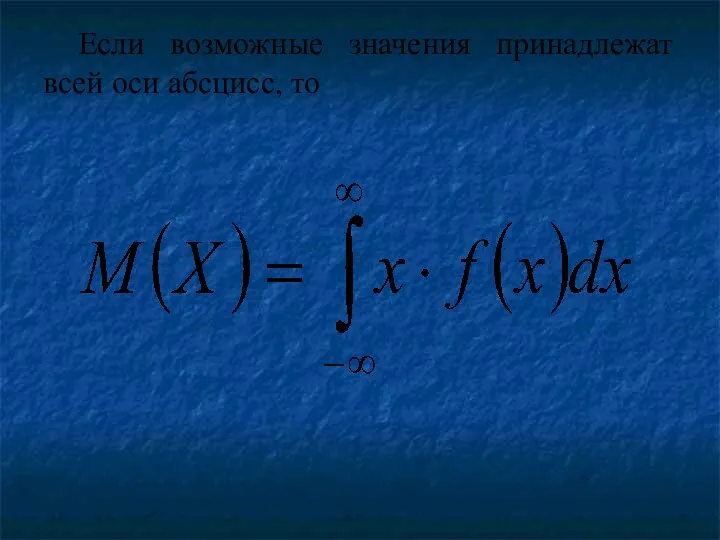


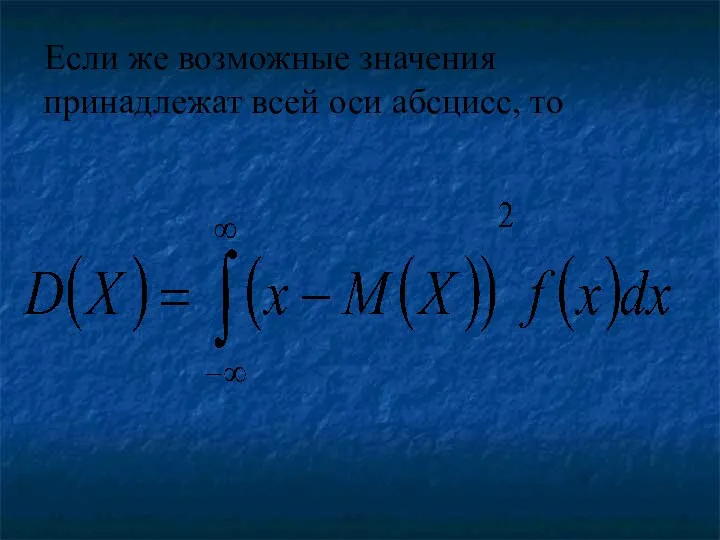




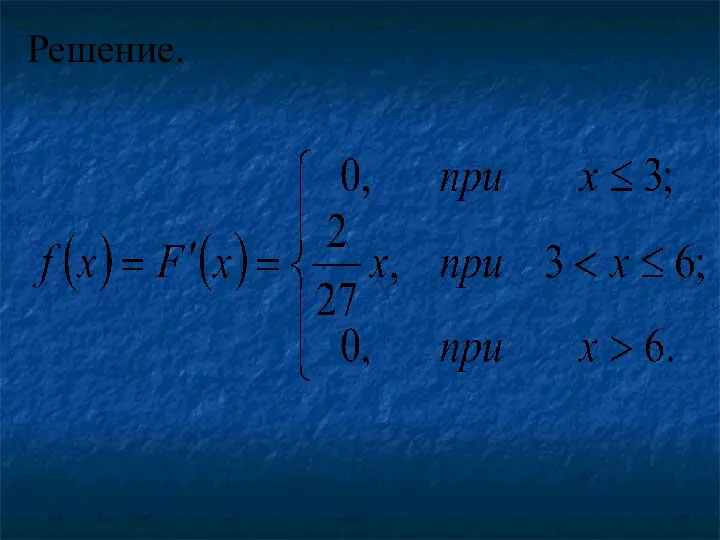
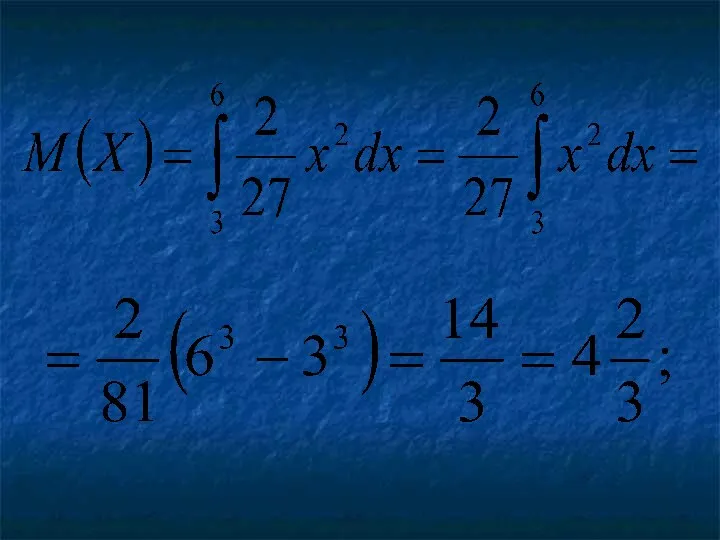
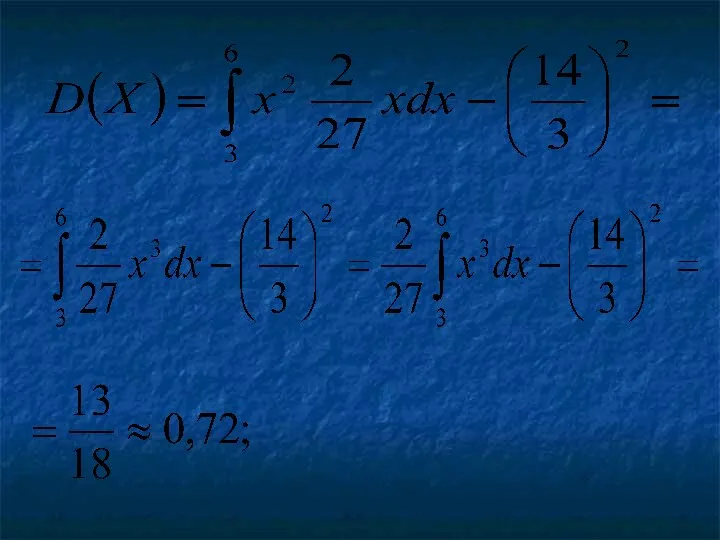
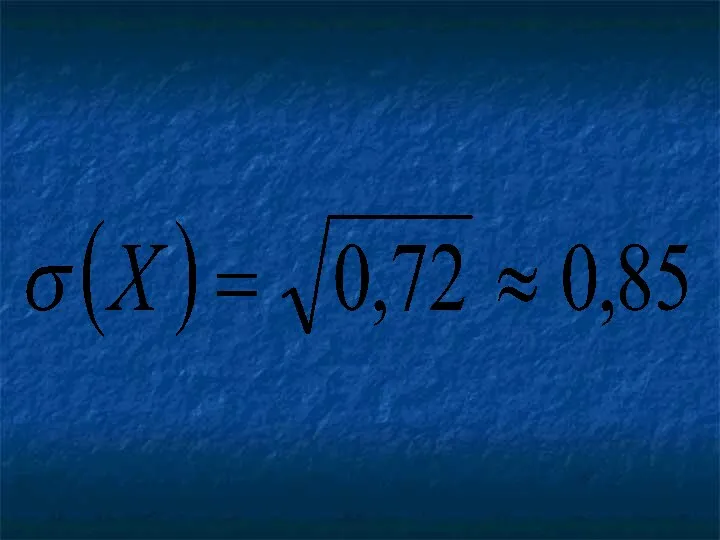





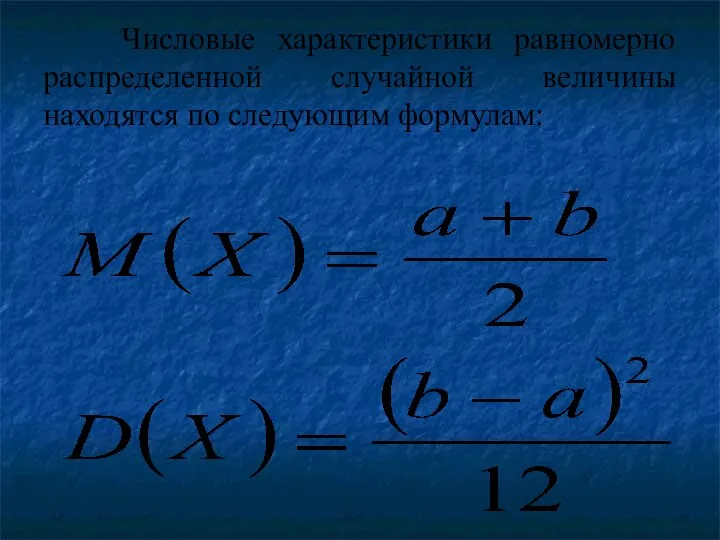

























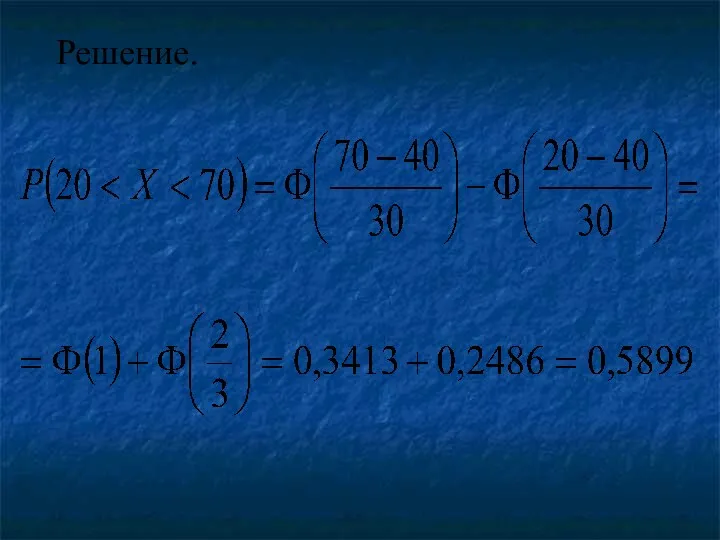

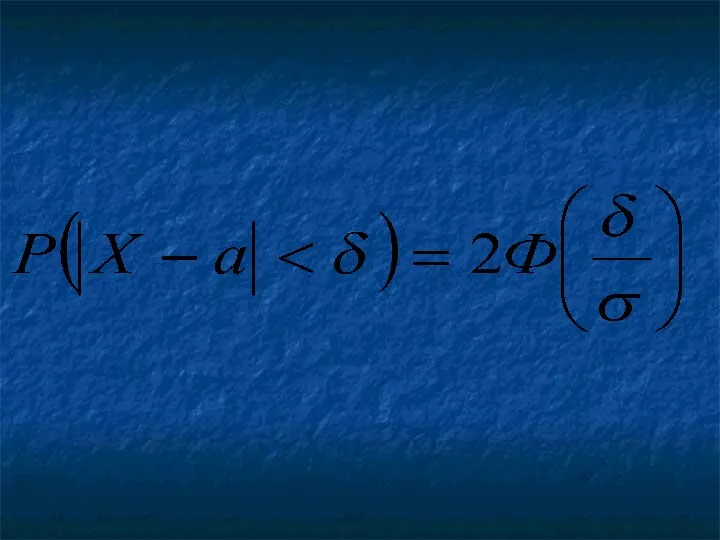


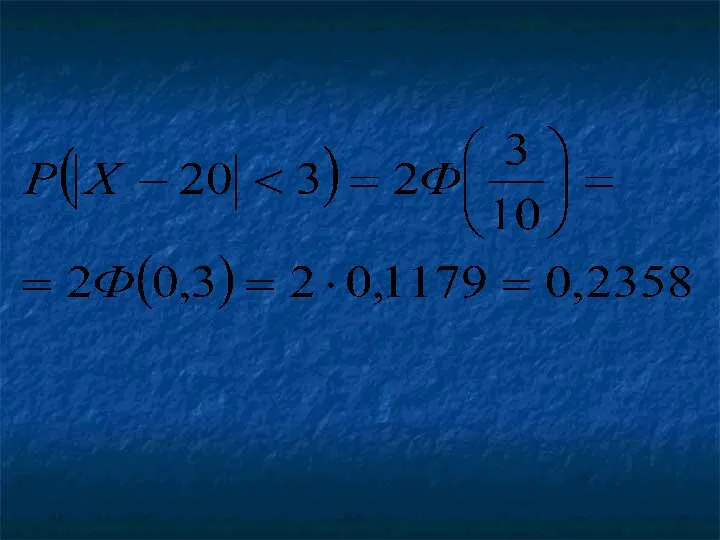

 Числовые выражения. 7 класс
Числовые выражения. 7 класс Формулы. Геометрия. (5 класс)
Формулы. Геометрия. (5 класс) мастер-класс для учителей начальной школы Магические квадраты
мастер-класс для учителей начальной школы Магические квадраты Формулы приведения
Формулы приведения Расположите однозначные ответы в порядке убывания. Доли. Обыкновенные дроби
Расположите однозначные ответы в порядке убывания. Доли. Обыкновенные дроби Перпендикулярность прямых и плоскостей. Повторение
Перпендикулярность прямых и плоскостей. Повторение Своя игра. Алгебра
Своя игра. Алгебра Действия с отрицательными и положительными числами на уроках математики и географии
Действия с отрицательными и положительными числами на уроках математики и географии Вектор. Определение. Длина (модуль) вектора
Вектор. Определение. Длина (модуль) вектора Множества и операции над множествами
Множества и операции над множествами Урок математики 3 класс Виды треугольников М.И. Моро
Урок математики 3 класс Виды треугольников М.И. Моро Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12)
Тени. Общие положения. Чертежи пространственных фигур. (Лекция 12) Статистические ряды распределения и их виды
Статистические ряды распределения и их виды Презентация Как люди научились считать
Презентация Как люди научились считать Деление с остатком
Деление с остатком Симметрия относительно плоскости
Симметрия относительно плоскости Деление и дроби
Деление и дроби Осевая и центральная симметрия. Урок геометрии в 8 классе
Осевая и центральная симметрия. Урок геометрии в 8 классе Признаки делимости
Признаки делимости Раскрытие скобок. Математика. 6 класс
Раскрытие скобок. Математика. 6 класс Алгебраические дроби, сокращение дробей. 7 класс
Алгебраические дроби, сокращение дробей. 7 класс Прямая и обратная пропорциональные зависимости. (6 класс)
Прямая и обратная пропорциональные зависимости. (6 класс) Случаи сложения вида +7
Случаи сложения вида +7 Дециметр и метр
Дециметр и метр Решение уравнений и систем уравнений в рамках подготовки к ЕГЭ
Решение уравнений и систем уравнений в рамках подготовки к ЕГЭ Выбор рационального принципа структурного построения объектов наземной космической инфраструктуры. Лекция 21
Выбор рационального принципа структурного построения объектов наземной космической инфраструктуры. Лекция 21 Вычисление площадей фигур на клетчатой бумаге. Формула Пика
Вычисление площадей фигур на клетчатой бумаге. Формула Пика Равнобедренные треугольники
Равнобедренные треугольники