Содержание
- 2. Определения Поле: (A,+,*,0,1) Кольцо с 1 * - коммутативно ∀ aОA\{0} ∃ a-1: aa-1 = 1
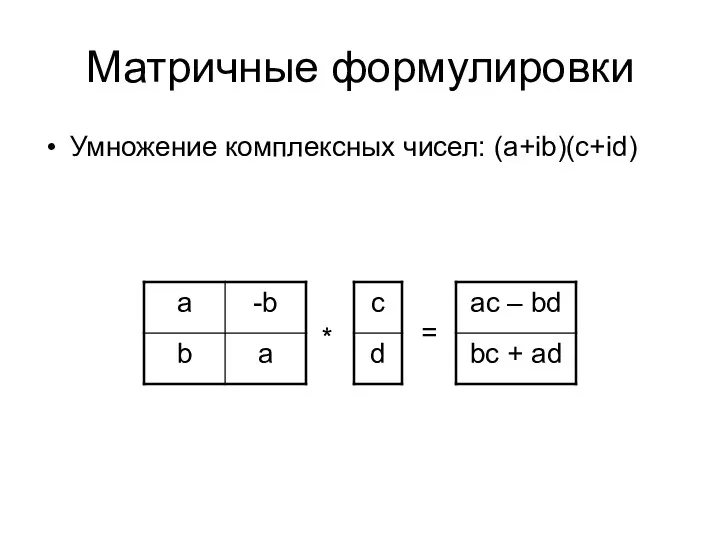
- 3. Матричные формулировки Умножение комплексных чисел: (a+ib)(c+id) * =
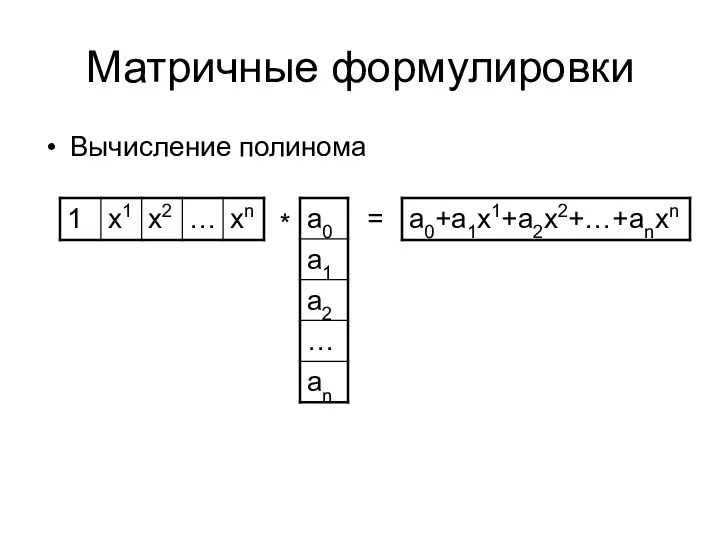
- 4. Матричные формулировки Вычисление полинома * =
- 5. Модель вычислений X = {x1,…,xn} – формальные переменные (параметры программы) Y = {y1,…,yn} – вспомогательные переменные
- 6. Термальное значение v : X ∪ Y → F[x1,…,xn] – значения переменных «в терминах» x1,…,xn. v(c)
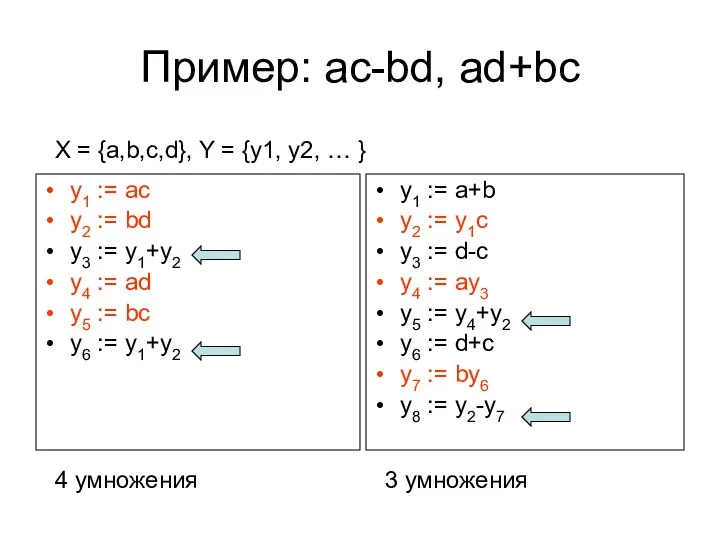
- 7. Пример: ac-bd, ad+bc y1 := ac y2 := bd y3 := y1+y2 y4 := ad y5
- 8. Определения Вектора v1,…,vk О Fm[a1,…,an] линейно-независимы по модулю Fm, если ∀ u1,…ukОF : (Σuivi О Fm
- 9. Теорема о нижней оценке (1) Теорема. Пусть M – (r×p)-матрица над F[a1,…,an], x=[x1,…,xp]T - столбец. Тогда,
- 10. Доказательство Пусть требуется s умножений e1,…,es - вычисляются на шагах с умножением Тогда Mx = Ne
- 11. Доказательство Пусть r>s (противное) Тогда строки N линейно-зависимы (в обычном смысле матриц над полем) То есть
- 12. Теорема о нижней оценке (2) Теорема. Пусть M – (r×p)-матрица над F[a1,…,an], x=[x1,…,xp]T – столбец, yОFp[a1,…,an].
- 13. Активное умножение - примеры
- 14. Доказательство (индукция) q = 1) Cуществует mijОF[a1,…,an] \ F Mx (а значит, и MX+y) содержит произведение
- 15. Доказательство (индукция) Шаг индукции: q>1 Пусть π – вычисление для Mx+y. По предположению индукции π содержит
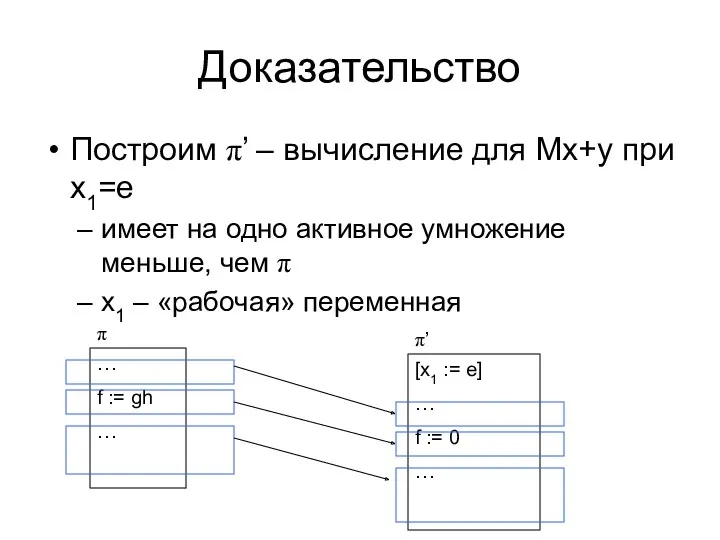
- 16. Доказательство Построим π’ – вычисление для Mx+y при x1=e имеет на одно активное умножение меньше, чем
- 17. Доказательство π’ вычисляет M’x’ + y’, причём ранг M’ по столбцам равен q-1 + M +
- 18. Доказательство π’ вычисляет M’x’ + y’, причём ранг M’ по столбцам равен q-1(докажем позже) + y’
- 19. Использованная лемма Лемма. Пусть задан набор векторов v1,…,vkОFm[a1,…,am]. Если среди них есть q линейно-независимых, то для
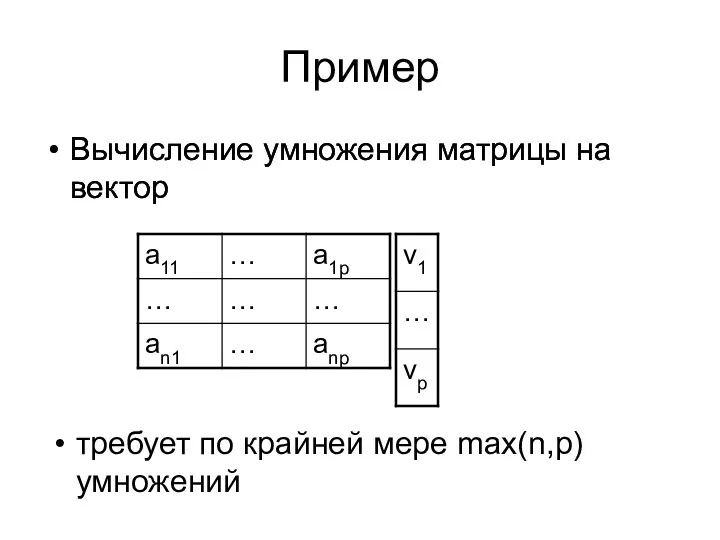
- 20. Пример Вычисление умножения матрицы на вектор Вычисление умножения матрицы на вектор требует по крайней мере max(n,p)
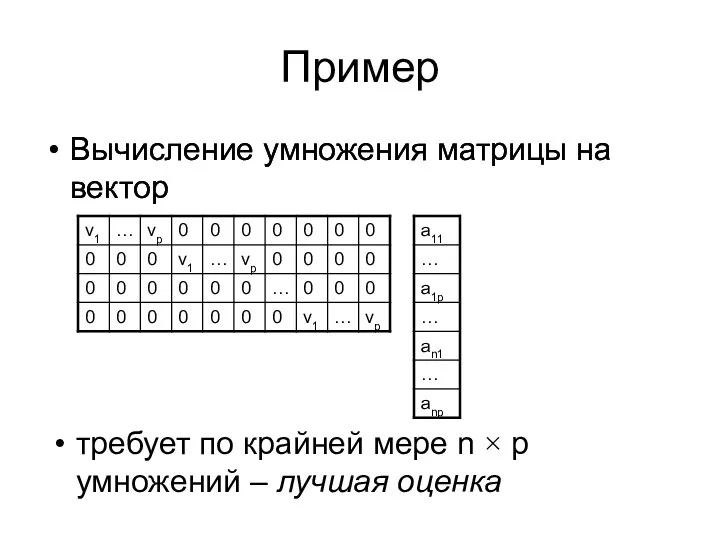
- 21. Пример Вычисление умножения матрицы на вектор Вычисление умножения матрицы на вектор требует по крайней мере n
- 23. Скачать презентацию


![Термальное значение v : X ∪ Y → F[x1,…,xn] –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591464/slide-5.jpg)
![Определения Вектора v1,…,vk О Fm[a1,…,an] линейно-независимы по модулю Fm, если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591464/slide-7.jpg)





![Доказательство (индукция) q = 1) Cуществует mijОF[a1,…,an] \ F Mx](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591464/slide-13.jpg)



![Использованная лемма Лемма. Пусть задан набор векторов v1,…,vkОFm[a1,…,am]. Если среди](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/591464/slide-18.jpg)
 Методы анализа данных. Примеры задач. Иллюстрации
Методы анализа данных. Примеры задач. Иллюстрации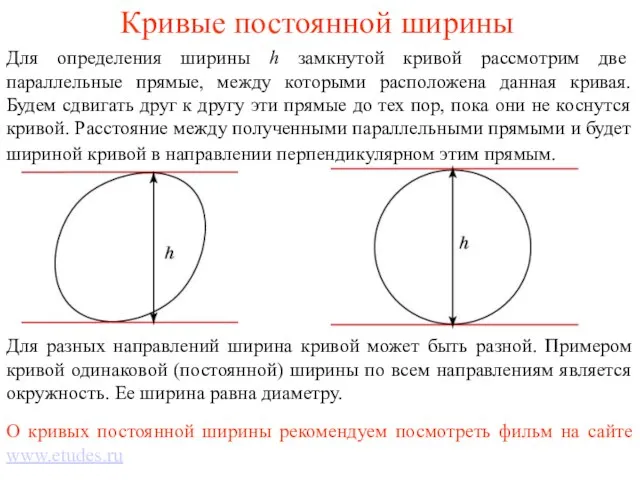 Кривые постоянной ширины
Кривые постоянной ширины Десятичные дроби произвольного знака
Десятичные дроби произвольного знака Прямоугольник, ромб, квадрат. Задания для устного счета. Упражнение 4. 8 класс
Прямоугольник, ромб, квадрат. Задания для устного счета. Упражнение 4. 8 класс Системы линейных алгебраических уравнений (лекция 1)
Системы линейных алгебраических уравнений (лекция 1) Сумма первых n членов арифметической прогрессии
Сумма первых n членов арифметической прогрессии Состав чисел второго десятка с переходом через десяток
Состав чисел второго десятка с переходом через десяток Лінійні рівняння, 7 клас
Лінійні рівняння, 7 клас Интерактивное учебное пособие. Помоги Незнайке
Интерактивное учебное пособие. Помоги Незнайке Задачі на відсотки
Задачі на відсотки Отношение соответствующих значений. Задачи
Отношение соответствующих значений. Задачи Обслуговування заявок за пріоритетними дисциплінами
Обслуговування заявок за пріоритетними дисциплінами Комплексные числа в алгебраической форме
Комплексные числа в алгебраической форме Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Математика 5 класс. Вычитание
Математика 5 класс. Вычитание Разложение на множители суммы и разности кубов
Разложение на множители суммы и разности кубов Формулы косинуса суммы и разности двух аргументов. 10 класс
Формулы косинуса суммы и разности двух аргументов. 10 класс Виды треугольников
Виды треугольников Pravilnye_Mnogogranniki
Pravilnye_Mnogogranniki Презентация к уроку математики Виды углов
Презентация к уроку математики Виды углов Геометрическая интерпретация комплексных чисел
Геометрическая интерпретация комплексных чисел Тригонометриялық теңдеулерді шешу
Тригонометриялық теңдеулерді шешу Умножение десятичной дроби на натуральное число. Урок математики в 5 классе
Умножение десятичной дроби на натуральное число. Урок математики в 5 классе Математический брейн-ринг для учащихся 6 классов
Математический брейн-ринг для учащихся 6 классов Признак параллельности прямой и плоскости
Признак параллельности прямой и плоскости Техника написания цифр
Техника написания цифр Теорема Пифагора – её история и значение
Теорема Пифагора – её история и значение