Содержание
- 2. Вычисление обратной матрицы Обратная матрица определена только для квадратных невырожденных матриц и вычисляется по формуле: где
- 3. § 4. Ранг матрицы Опр. 1. Рангом матрицы А называется порядок наибольшего отличного от нуля минора
- 4. Вычисление ранга матрицы с помощью элементарных преобразований Элементарные преобразования матрицы: 1. транспонирование; 2. перестановка строк (столбцов);
- 5. Теорема 1. Элементарные преобразования матрицы не меняют её ранга. Теорема 2. Ранг ступенчатой матрицы равен числу
- 6. Понятие линейной комбинации и линейной зависимости Опр 3. Линейной комбинацией системы x1,…xn наз. сумма a1x1+a2x2+…anxn, где
- 7. Теорема о ранге матрицы Ранг матрицы равен максимальному числу линейно независимых строк( столбцов) матрицы.
- 8. § 5. Система линейных алгебраических уравнений (СЛАУ) Опр. 1. Системой m линейных алгебраических уравнений с n
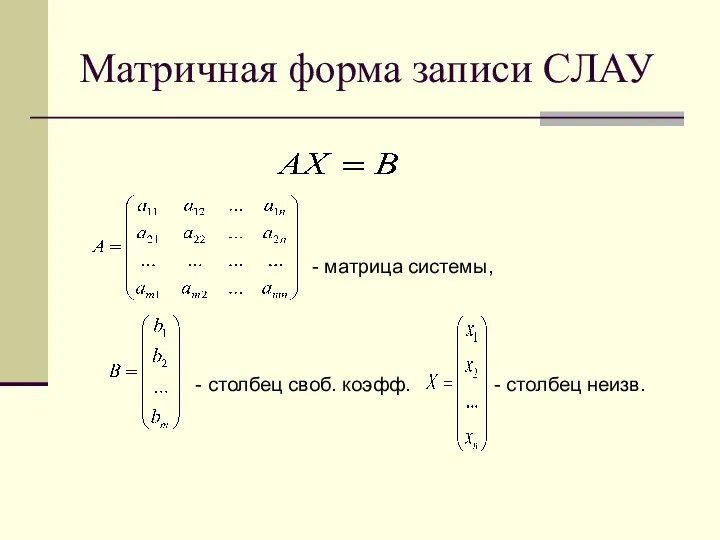
- 9. Матричная форма записи СЛАУ - матрица системы, - столбец своб. коэфф. - столбец неизв.
- 10. Расширенная матрица системы Опр. 2. Матрица, полученная из м. А добавлением справа столбца свободных членов, называется
- 11. Опр. 3. Решением системы AX=B называется упорядоченное множество чисел , удовлетворяющих всем его уравнениям СЛАУ по
- 12. Опр. 4. Две СЛАУ называются равносильными, если они имеют одно и то же множество решений. Теорема
- 13. Неоднородные и однородные СЛАУ СЛАУ делятся на два типа по виду правой части: 1. AX=0 –
- 14. Миноры: произвольные, дополнительные, базисные Опр 5. Минором порядка n произвольной матрицы A называется определитель M*, расположенный
- 15. Базисный минор Опр 7. В матрице А минор М* порядка r называется базисным, если он отличен
- 16. Теорема о базисном миноре В произвольной матрицу А каждый столбец(строка) является линейной комбинацией столбцов (строк), в
- 17. Следствие 2. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов этой
- 18. Однородные СЛАУ Если свободные члены всех уравнений равны нулю, то система наз. однородной.
- 19. Совместность однородных СЛАУ Однородные СЛАУ всегда совместны: – нулевое (тривиальное) решение. Если у однородной системы ,
- 20. Фундаментальная система решений однородной СЛАУ (ФСР) Теорема 1. Если однородная СЛАУ имеет два решения, то любая
- 21. или
- 22. Теорема 2. Если ранг однородной СЛАУ равен r, то СЛАУ имеет n-r линейно независимых решений. Теорема
- 24. Скачать презентацию


















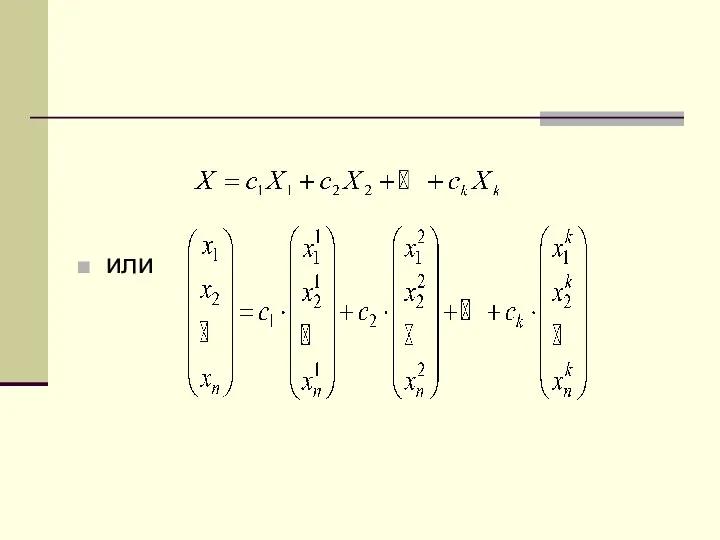

 Числовые и буквенные выражения
Числовые и буквенные выражения Внеклассное мероприятие для 8 класса по геометрии По следам Пифагора
Внеклассное мероприятие для 8 класса по геометрии По следам Пифагора Численное решение нелинейных уравнений
Численное решение нелинейных уравнений Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Решение логарифмических уравнений
Решение логарифмических уравнений Площади фигур
Площади фигур Сложение и умножение дробей с одинаковыми знаменателями. Технологическая карта урока по математике в 5 классе
Сложение и умножение дробей с одинаковыми знаменателями. Технологическая карта урока по математике в 5 классе Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Некоторые приемы запоминания тригонометрических формул. 10 класс
Некоторые приемы запоминания тригонометрических формул. 10 класс Открытый урок по русскому языку на тему Правописание парных согласных на конце слова - 2 класс, школа россии
Открытый урок по русскому языку на тему Правописание парных согласных на конце слова - 2 класс, школа россии Углы. Открытый банк заданий по математике. Задачи
Углы. Открытый банк заданий по математике. Задачи Числовые промежутки
Числовые промежутки Математическая сказка. 3 класс
Математическая сказка. 3 класс Аксиомы стереомотрии
Аксиомы стереомотрии Объем пирамиды. Инструкция по решению задач
Объем пирамиды. Инструкция по решению задач Окружность и её элементы
Окружность и её элементы Презентация к уроку математики. Понятие задачи
Презентация к уроку математики. Понятие задачи Начертательная геометрия. Инженерная графика
Начертательная геометрия. Инженерная графика Число и цифра 5. Состав Числа 5.
Число и цифра 5. Состав Числа 5. Внеклассное занятие по математике. Тема:Время
Внеклассное занятие по математике. Тема:Время Во сколько раз больше или меньше
Во сколько раз больше или меньше Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 5
Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 5 Найди частное
Найди частное Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Перенос графика функции у=ах2 вдоль осей координат
Перенос графика функции у=ах2 вдоль осей координат Меры длины
Меры длины Поразрядный способ сравнения десятичных дробей
Поразрядный способ сравнения десятичных дробей Взаємозв'язок ділення і множення. 2 клас
Взаємозв'язок ділення і множення. 2 клас