Содержание
- 2. 1. Определение обратной матрицы Необходимо: матрица должна быть квадратной. Матрица называется обратной по отношению к матрице
- 3. 2. Способы нахождения обратной матрицы Алгоритм нахождения обратной матрицы: Вычисление определителя матрицы А, Построение матрицы алгебраических
- 4. Обращение матрицы можно осуществить по следующему правилу. 1. Вычислить определитель исходной матрицы Δ = det A.
- 5. Пример 1.10. Произвести обращение матрицы и доказать, что она обратная. Решение
- 6. Доказательство: Если A-1 – обратная матрица, то справедливо выражение AA-1 = E.
- 7. Действия над матрицами Нахождение обратной матрицы Обратная матрица обозначается символом А-1. Таким образом, согласно определению: АА-1=А-1А=Е.
- 8. Действия над матрицами Из второй строки вычтем первую строку Разложим определитель по элементам 3 столбца -2
- 9. Алгоритм нахождения обратной матрицы (Метод Гаусса): К матрице А справа приписывается Е, Проделывая преобразования над строками
- 10. 3. Ранг матрицы
- 11. Ранг матрицы (1) Минором к – го порядка матрицы А называется определитель к – го порядка
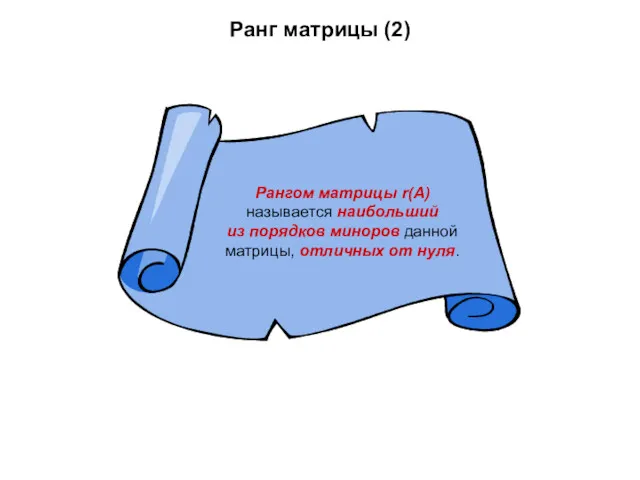
- 12. Ранг матрицы (2)
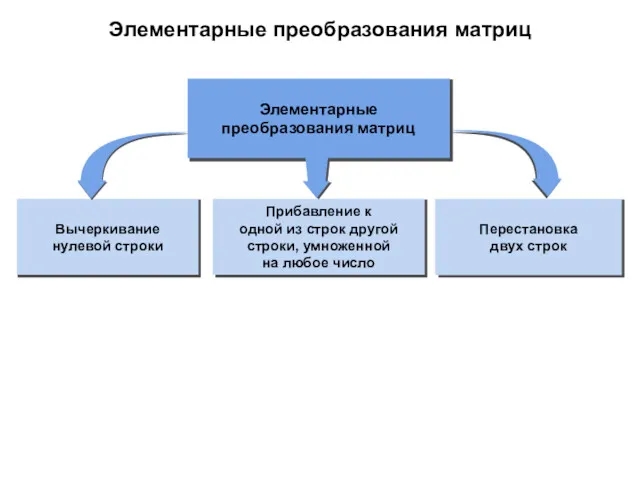
- 13. Элементарные преобразования матриц Вычеркивание нулевой строки Элементарные преобразования матриц Перестановка двух строк Прибавление к одной из
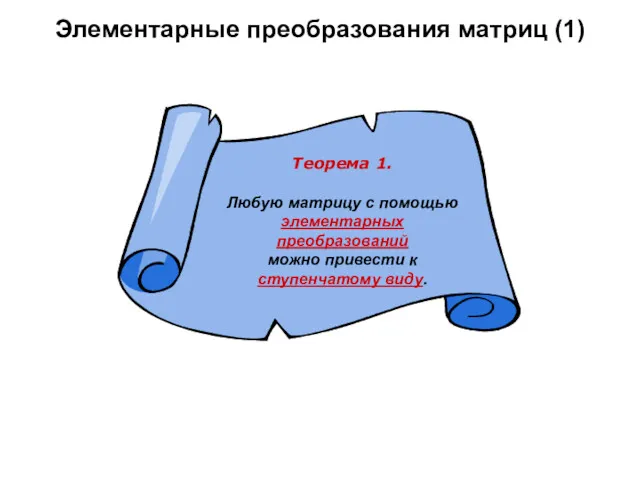
- 14. Элементарные преобразования матриц (1)
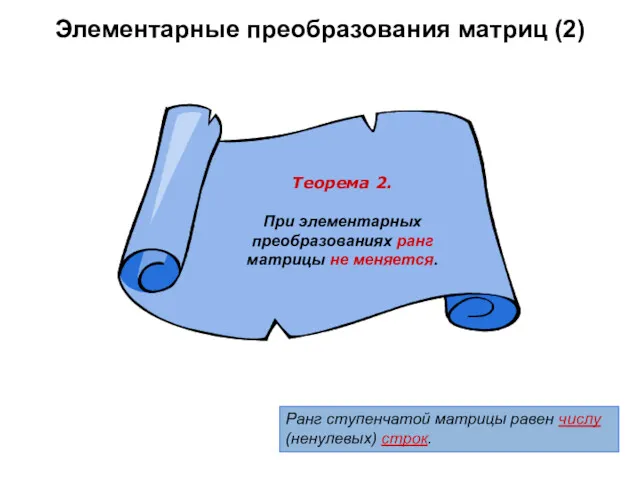
- 15. Элементарные преобразования матриц (2) Ранг ступенчатой матрицы равен числу (ненулевых) строк.
- 16. Пример 6 (1) Найти ранг матрицы:
- 17. Пример 6 (2) Решение. Приведем матрицу к ступенчатому виду: ·(-2) ↓ ←⊕
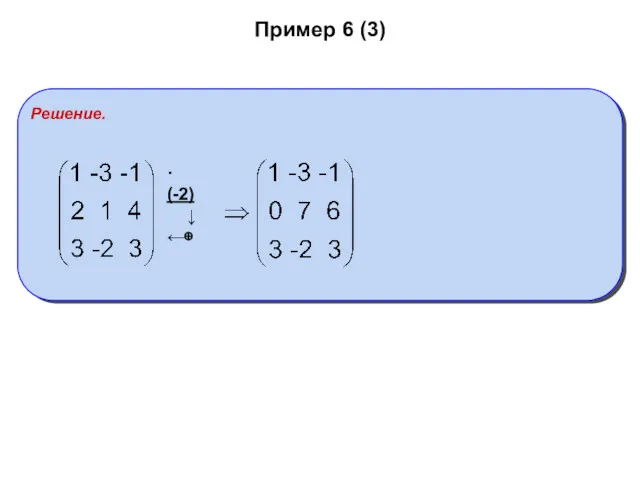
- 18. Пример 6 (3) Решение. ·(-2) ↓ ←⊕
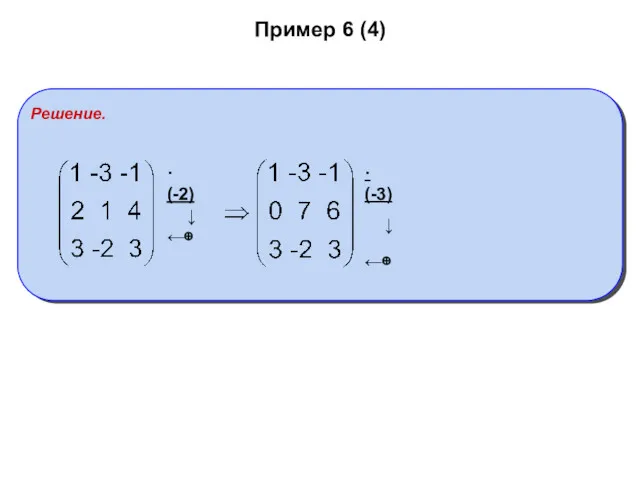
- 19. Пример 6 (4) Решение. ·(-2) ↓ ←⊕ ·(-3) ↓ ←⊕
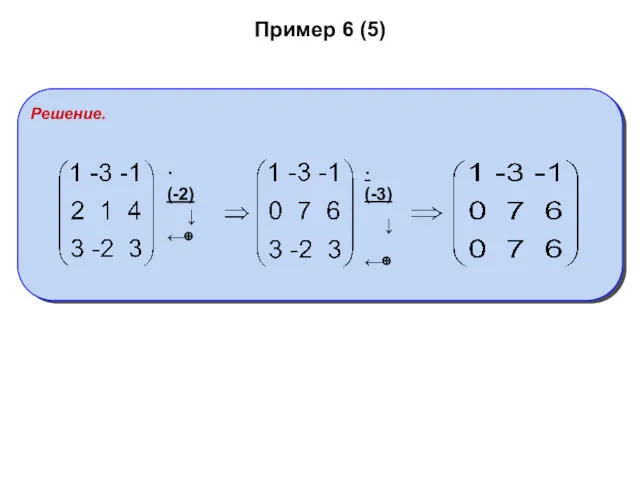
- 20. Пример 6 (5) Решение. ·(-2) ↓ ←⊕ ·(-3) ↓ ←⊕
- 21. Пример 6 (6) Решение.
- 22. Пример 6 (7) Решение. r(A)=2
- 23. 3. Ранг матрицы, способы нахождения ранга матрицы Рангом матрицы называют наибольший из порядков ее миноров, отличных
- 25. Скачать презентацию















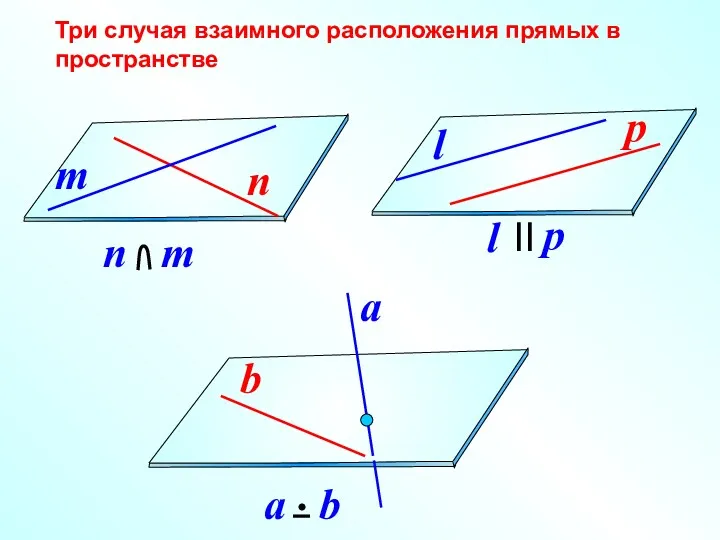 Параллельность прямой и плоскости
Параллельность прямой и плоскости Фрагмент уроку математики. Каліграфічна хвилинка
Фрагмент уроку математики. Каліграфічна хвилинка Волшебство чисел. Закон девятки
Волшебство чисел. Закон девятки Математика вокруг нас
Математика вокруг нас Наименьшее общее кратное
Наименьшее общее кратное Старинные русские меры длины и веса
Старинные русские меры длины и веса Дидактические игры на уроках математики
Дидактические игры на уроках математики Функция y=sin x, её свойства и график
Функция y=sin x, её свойства и график Математика в жизни человека
Математика в жизни человека Комплексные числа
Комплексные числа Принцип Дирихле
Принцип Дирихле Дискриминант квадратных уравнений
Дискриминант квадратных уравнений Приемы устного счета
Приемы устного счета Неравенство треугольника
Неравенство треугольника Сложение и вычитание смешанных чисел (урок математики в 6 классе)
Сложение и вычитание смешанных чисел (урок математики в 6 классе) Задачи на готовых чертежах Смежные и вертикальные углы
Задачи на готовых чертежах Смежные и вертикальные углы Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Правильные многоугольники
Правильные многоугольники Умножение и деление на однозначное число
Умножение и деление на однозначное число Урок математики. Многозначные числа и действия с ними.
Урок математики. Многозначные числа и действия с ними. Веселый счет
Веселый счет Первый урок алгебры в 7 классе
Первый урок алгебры в 7 классе Отрезок. Длина отрезка
Отрезок. Длина отрезка Противоположные числа
Противоположные числа Метр — одиниця довжини
Метр — одиниця довжини Решение простейших тригонометрических уравнений - 2
Решение простейших тригонометрических уравнений - 2 Функция арифметического квадратного корня, её свойства и график
Функция арифметического квадратного корня, её свойства и график Свойства квадратного корня
Свойства квадратного корня