Содержание
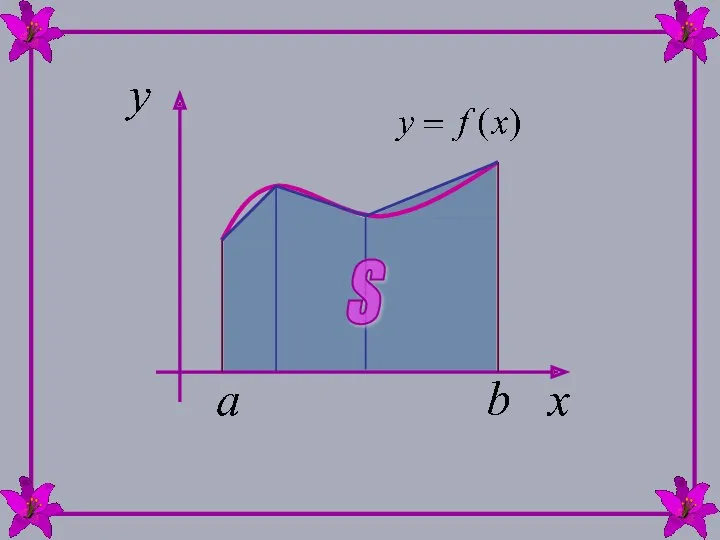
- 2. 1. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Пусть на отрезке [a,b] задана неотрицательная функция y=f(x). Требуется найти площадь криволинейной
- 3. Фигура под ломаной состоит из трапеций и ее площадь равна сумме площадей всех трапеций: Причем, площадь
- 4. S
- 5. За искомую площадь под кривой берут предел площади под ломаной при условии, что ломаная неограниченно приближается
- 6. Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] .
- 7. Интегральная сумма зависит от способа разбиения отрезка и выбора точек ξi Каждое отдельное слагаемое в интегральной
- 9. Наибольший из отрезков разбиения обозначим как Вся интегральная сумма будет равна
- 10. Если существует конечный предел интегральной суммы при не зависящий от способа разбиения отрезка [a,b] и выбора
- 11. Функция y=f(x) называется интегрируемой на отрезке [a,b]. Числа a и b называются нижним и верхним пределом,
- 12. Неопределенный интеграл есть семейство функций, а определенный интеграл есть определенное число. По определению предполагается, что а
- 13. С учетом этого несущественно, какой предел больше или меньше. Если а = b, то
- 14. Необходимое условие существования определенного интеграла 2. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Интегрируемая на отрезке [a,b] функция y=f(x) ограничена
- 15. Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция y=f(x) непрерывна, то она интегрируема на
- 16. Свойства определенного интеграла 1 Постоянный множитель можно выносить за знак определенного интеграла.
- 17. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим интегральную сумму: Переходим к пределу в
- 18. Следовательно по определению:
- 19. 2 Определенный интеграл от алгебраической суммы (разности) двух функций равен сумме (разности) интегралов от этих функций.
- 20. 3 Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов по
- 21. Геометрически это означает, что если a
- 22. S S S
- 23. 4 Если на [a,b], где a то
- 24. Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек то для интегральных сумм: Если Переходим к
- 25. Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда
- 26. Доказательство: По свойству 4 имеем: По свойству 1 и геометрическому смыслу определенного интеграла:
- 27. 5 Если на [a,b], где a Теорема о среднем что
- 28. Доказательство: По свойству функции, непрерывной на отрезке, для произвольного значения справедливо неравенство: Где m и М
- 29. Но функция, непрерывная на отрезке, принимает любое значение, заключенное между ее наименьшим и наибольшим значениями, поэтому
- 30. Пусть Тогда теорема о среднем утверждает, что найдется такая точка что площадь под кривой y=f(x) на
- 32. Равенство называется формулой среднего значения. называется средним значением функции.
- 34. Скачать презентацию
![1. ПОНЯТИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Пусть на отрезке [a,b] задана неотрицательная](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-1.jpg)


![Сумму вида называют интегральной суммой для функции y=f(x) на отрезке [a,b] .](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-5.jpg)




![Функция y=f(x) называется интегрируемой на отрезке [a,b]. Числа a и](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-10.jpg)



![Достаточное условие существования определенного интеграла Если на отрезке [a,b] функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-14.jpg)

![Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек Рассмотрим](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-16.jpg)




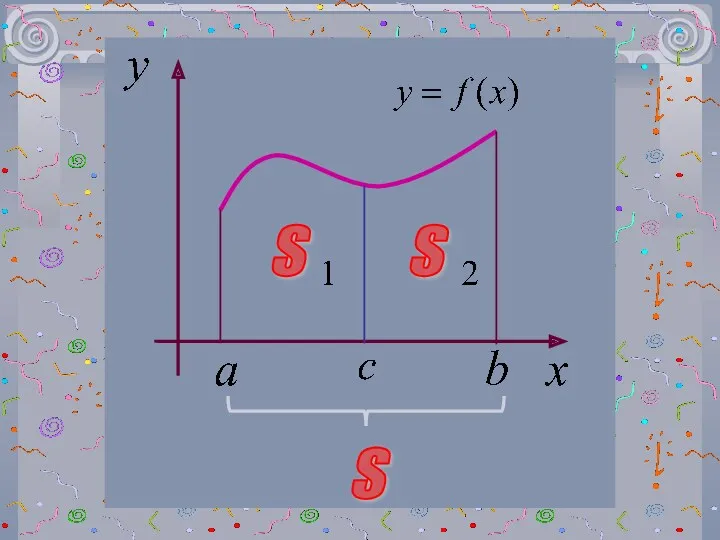
![4 Если на [a,b], где a то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-22.jpg)
![Доказательство: Пусть фиксировано разбиение отрезка [a,b] и выбор точек то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-23.jpg)
![Следствие. Пусть на [a,b], где a где m и M некоторые числа. Тогда](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-24.jpg)

![5 Если на [a,b], где a Теорема о среднем что](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396995/slide-26.jpg)





 Обыкновенные дроби
Обыкновенные дроби Умножение и деление десятичных дробей на натуральное число
Умножение и деление десятичных дробей на натуральное число Смежные и вертикальные углы. (7 класс)
Смежные и вертикальные углы. (7 класс) Презентация Состав чисел первого десятка
Презентация Состав чисел первого десятка Прямоугольные треугольники. Задания для устного счета
Прямоугольные треугольники. Задания для устного счета Число Пи
Число Пи Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Уравнения. Решение задач с помощью уравнений. 6 класс
Уравнения. Решение задач с помощью уравнений. 6 класс Інтегрований урок з математики та інформатики
Інтегрований урок з математики та інформатики Равные множества.
Равные множества. Трапеция. Геометрия 8 класс
Трапеция. Геометрия 8 класс Умножение и деление на 10
Умножение и деление на 10 Решение показательных уравнений
Решение показательных уравнений Решение уравнений. 5 класс
Решение уравнений. 5 класс Математический брейн-ринг
Математический брейн-ринг Презентация к уроку Числа 1 - 5
Презентация к уроку Числа 1 - 5 Тригонометрические уравнения sin x=a, cos x=a ,tg x=a, ctg x=a
Тригонометрические уравнения sin x=a, cos x=a ,tg x=a, ctg x=a Математика в профессии электрика
Математика в профессии электрика Геометрия и ландшафтный дизайн
Геометрия и ландшафтный дизайн Математика и здоровье
Математика и здоровье Окружность и круг. Сфера и шар
Окружность и круг. Сфера и шар Методы статистической обработки результатов активного и пассивного эксперимента. Погрешности измерений
Методы статистической обработки результатов активного и пассивного эксперимента. Погрешности измерений Финансовая математика
Финансовая математика Теория вероятностей; геометрическая вероятность; неравенство Чебышева
Теория вероятностей; геометрическая вероятность; неравенство Чебышева Сетевые задачи дискретной математики. Тема 5
Сетевые задачи дискретной математики. Тема 5 01-Формула суммы п первых членов арифметической прогрессии
01-Формула суммы п первых членов арифметической прогрессии Математика. Устный счёт. Сложение и вычитание.
Математика. Устный счёт. Сложение и вычитание. Вервейн. Алгоритм сложения трёхзначных чисел столбиком
Вервейн. Алгоритм сложения трёхзначных чисел столбиком