Оптимизация химикотехнологичеких процессов. Безусловная оптимизация методом классического математического анализа презентация
Содержание
- 2. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП Оптимизация ХТП – это достижение наилучших результатов функционирования ХТП (Химико-Технологического Процесса)в смысле
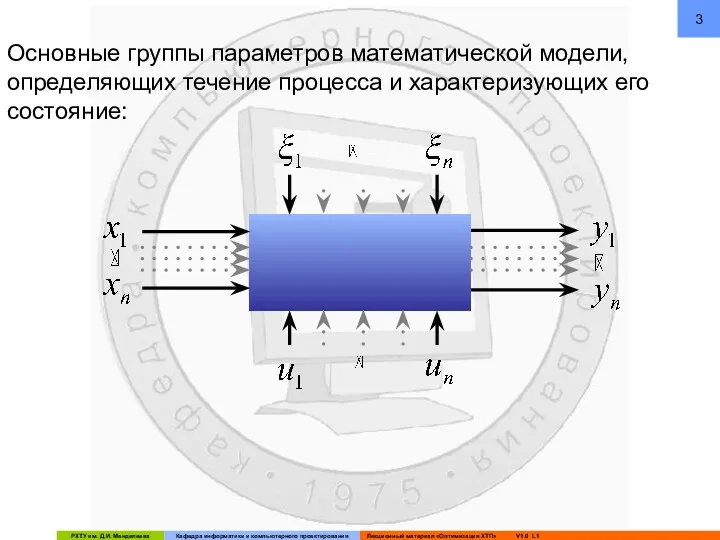
- 3. Основные группы параметров математической модели, определяющих течение процесса и характеризующих его состояние:
- 4. - Входные параметры (влияющие на состояние процесса, но на которые нельзя воздействовать) - Управляющие(оптимизирующие) параметры –
- 5. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП Математическая модель детерминированного процесса, которая может быть реализована на компьютере с применением
- 6. Решение задачи оптимизации – определение наименьшего (в частном случае, min )или наибольшего (в частном случае, max)
- 7. ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП Таким образом, задача оптимизации может быть решена с применением компьютера только тогда,
- 8. Однако так как на входные параметры нельзя воздействовать, они не могут быть оптимизирующими или управляющими параметрами.
- 9. Если в дальнейшем принять, что , то формулировка задачи оптимизации имеет вид и, в общем случае,
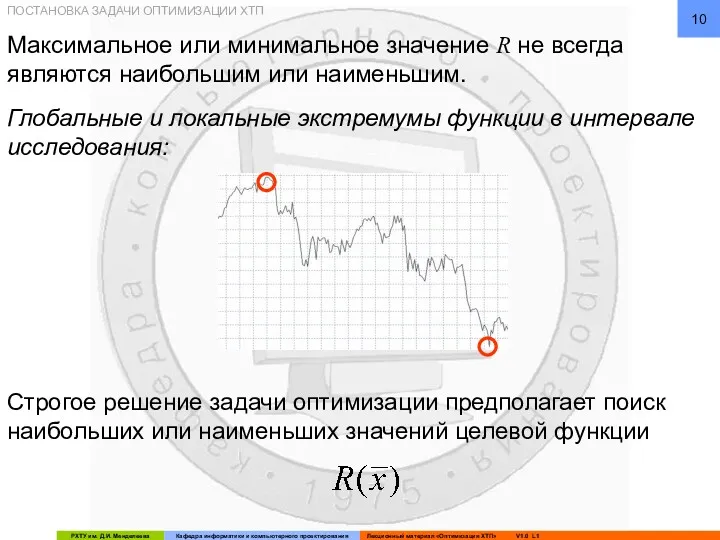
- 10. Максимальное или минимальное значение R не всегда являются наибольшим или наименьшим. Глобальные и локальные экстремумы функции
- 11. ИССЛЕДОВАНИЕ ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДОМ КЛАССИЧЕСКОГО МАТЕМАТИЧЕСКОГО АНАЛИЗА Методы исследования функций классического анализа могут применяться в случае,
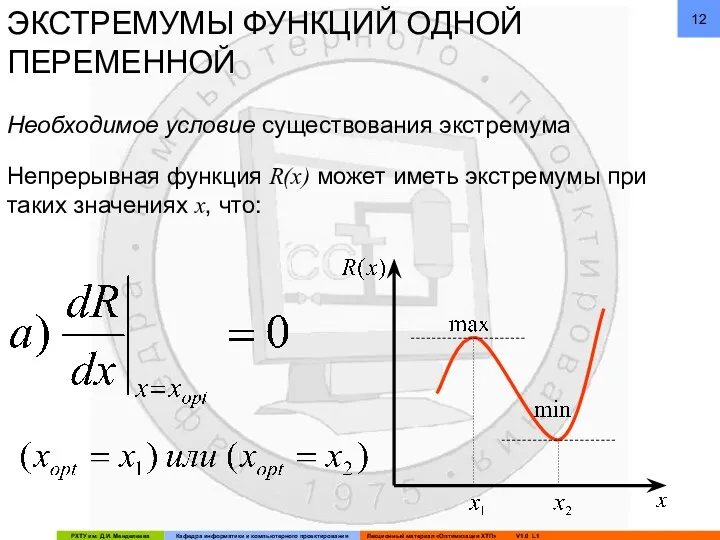
- 12. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Непрерывная функция R(x) может иметь экстремумы при таких значениях x, что: Необходимое
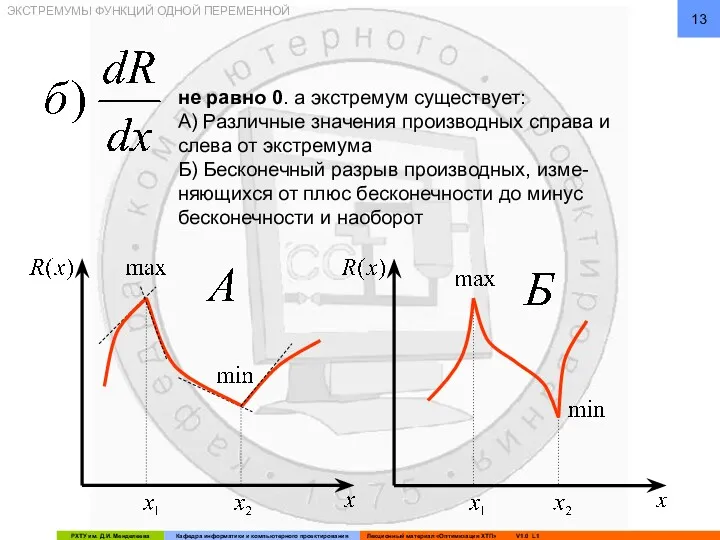
- 13. не равно 0. а экстремум существует: А) Различные значения производных справа и слева от экстремума Б)
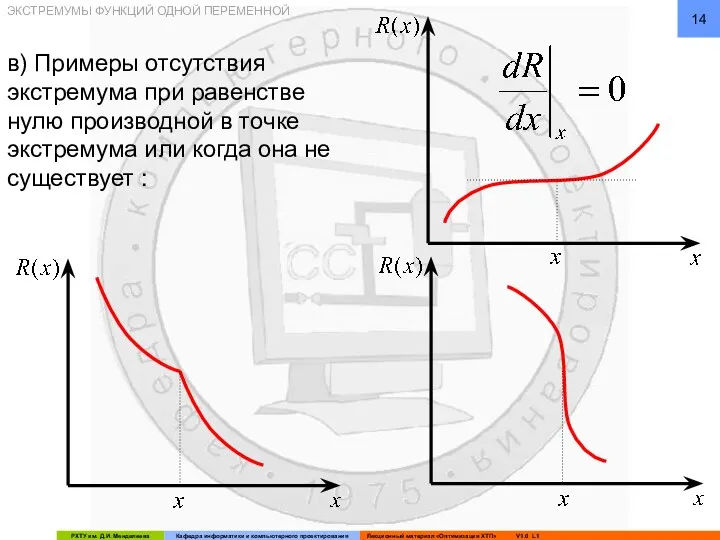
- 14. в) Примеры отсутствия экстремума при равенстве нулю производной в точке экстремума или когда она не существует
- 15. Для подтверждения наличия экстремумов в определенных точках необходимо проводить дополнительные исследования: Сравнение значений функции справа и
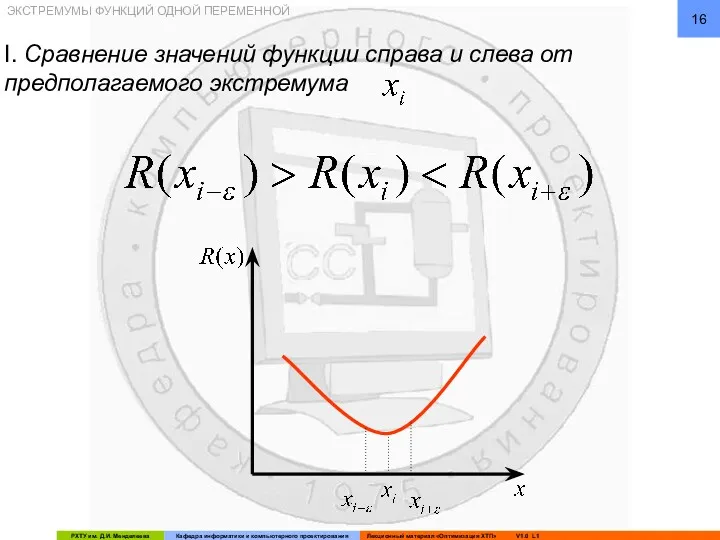
- 16. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ I. Сравнение значений функции справа и слева от предполагаемого экстремума
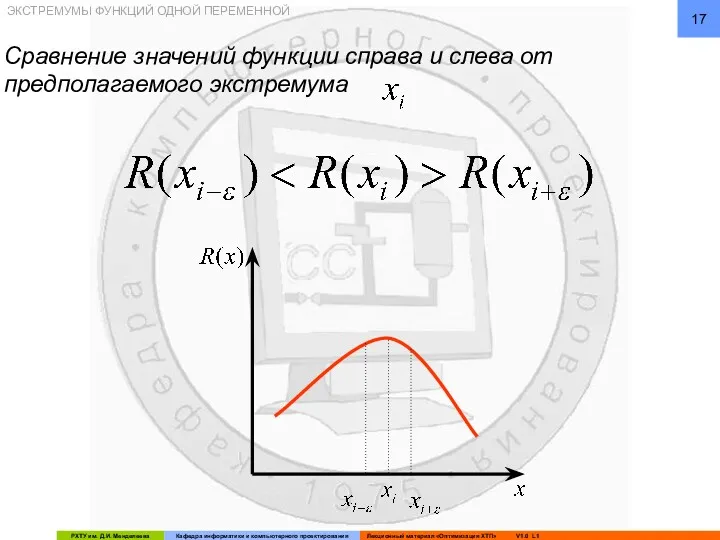
- 17. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Сравнение значений функции справа и слева от предполагаемого экстремума
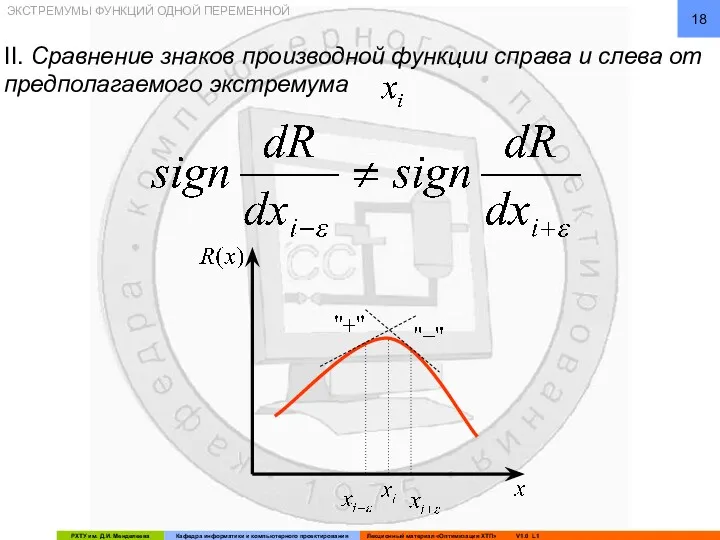
- 18. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ II. Сравнение знаков производной функции справа и слева от предполагаемого экстремума
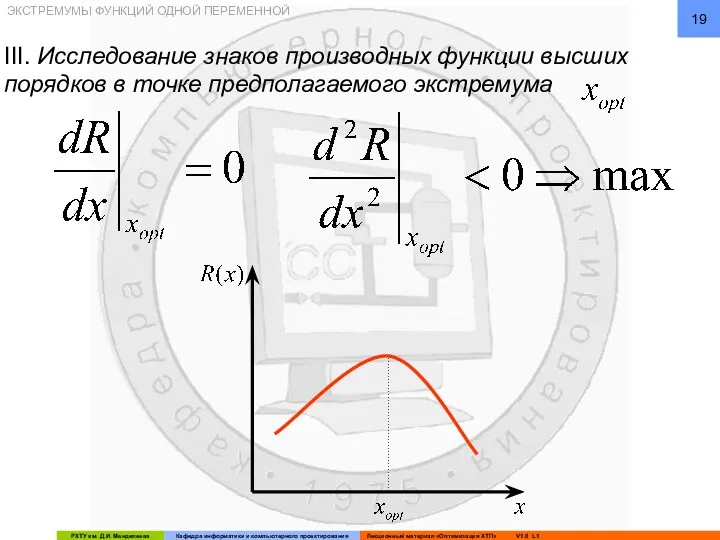
- 19. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ III. Исследование знаков производных функции высших порядков в точке предполагаемого экстремума
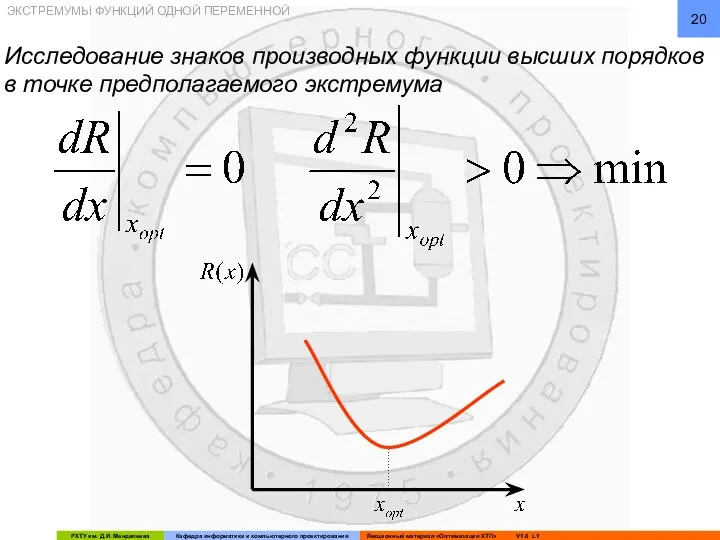
- 20. ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Исследование знаков производных функции высших порядков в точке предполагаемого экстремума
- 21. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Функция многих переменных имеет в точке максимум (минимум), если существует такая окрестность
- 22. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Необходимым условием существования экстремума функции многих переменных в точке является равенство нулю
- 23. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Равнозначным условием является условие равенства нулю полного дифференциала дифференцируемой функции в точке
- 24. Разложив функцию в окрестности точки в ряд Тейлора по степеням : ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Достаточные
- 25. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ с учётом необходимого условия существования экстремума:
- 26. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Если выражение сохраняет один и тот же знак для любых приращений то
- 27. Приращение целевой функции в окрестности экстремума определяется
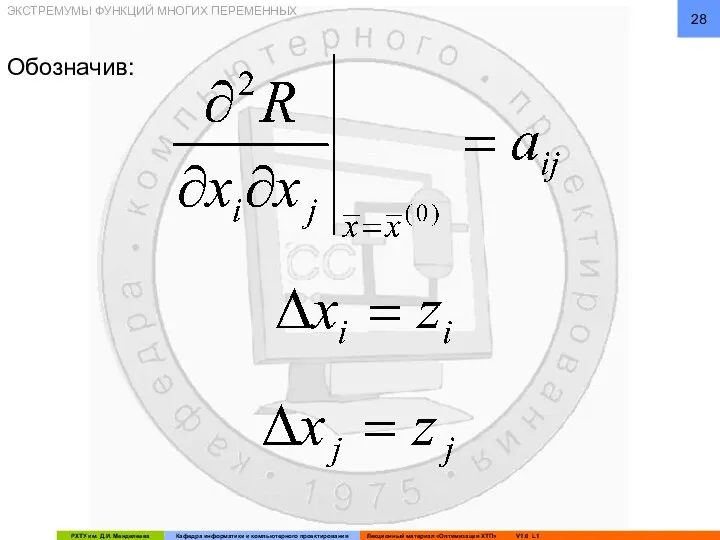
- 28. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Обозначив:
- 29. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ получаем выражение вида: где - квадратичная форма.
- 30. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Условие положительной определённости квадратичной формы (достаточных условий существования минимума): при любых значениях
- 31. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Квадратичная форма будет положительно определённой, если все определители, составленные из элементов положительны
- 32. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Все определители Сильвестра положительны (положительно определенная
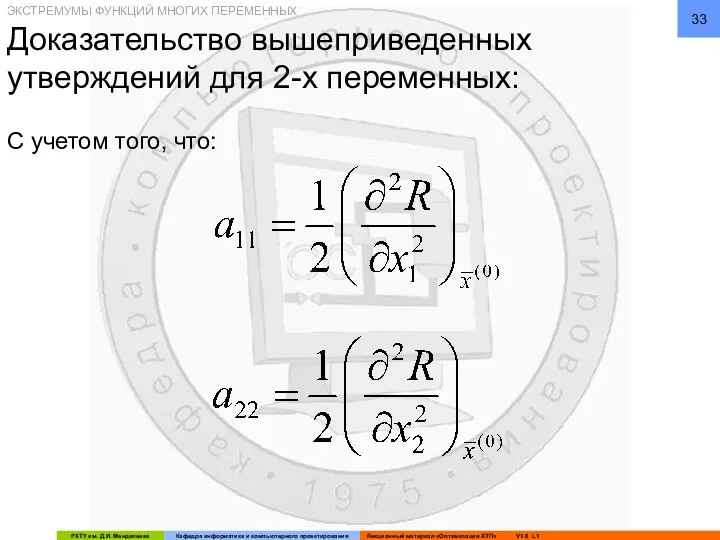
- 33. Доказательство вышеприведенных утверждений для 2-х переменных: С учетом того, что: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 34. и: Квадратичная форма второго порядка записывается: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 35. Преобразование последнего выражения приводит к соотношению: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 36. Отсюда следует: Квадратичная форма будет положительно определенной, если: и: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 37. Или в соответствии с условиями Сильвестра: и: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
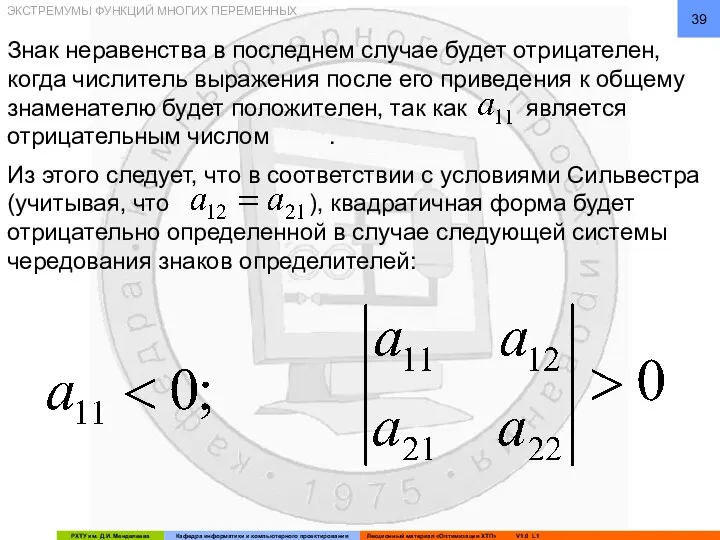
- 38. Квадратичная форма будет отрицательно определенной, если: и: ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 39. Знак неравенства в последнем случае будет отрицателен, когда числитель выражения после его приведения к общему знаменателю
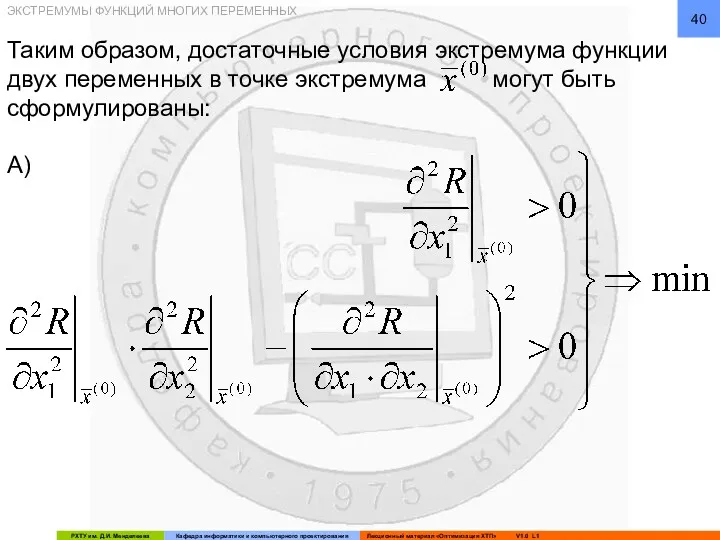
- 40. Таким образом, достаточные условия экстремума функции двух переменных в точке экстремума могут быть сформулированы: А) ЭКСТРЕМУМЫ
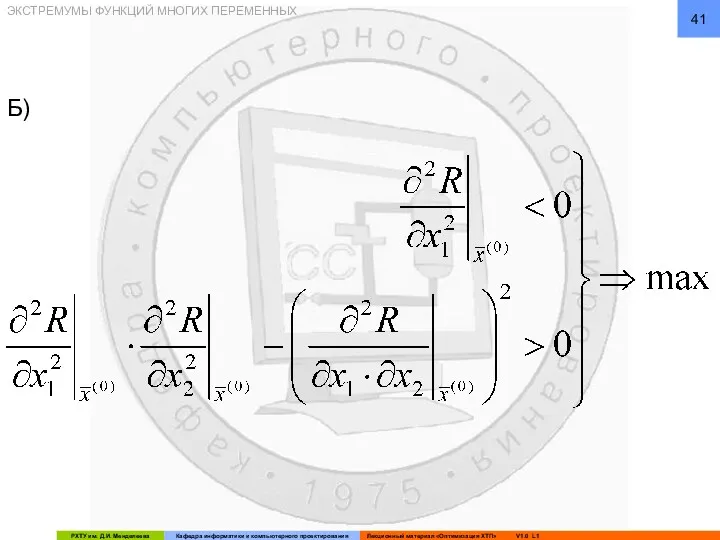
- 41. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Б)
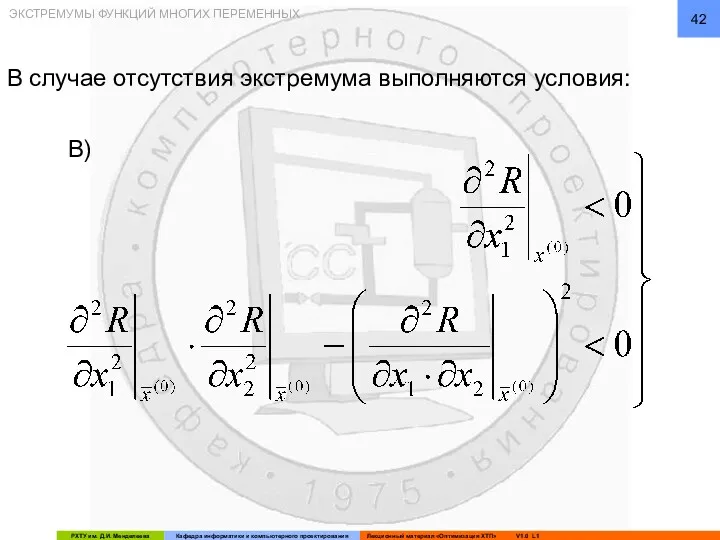
- 42. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ В случае отсутствия экстремума выполняются условия: В)
- 43. ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ Следует отметить, что аналитическая проверка достаточных условий экстремума функции многих переменных не
- 44. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ Рассмотрим химическую реакцию с целевым продуктом P, проходящую по схеме:
- 45. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ Скорость реакции по целевому продукту выражается по закону действующих масс: Необходимо определить
- 46. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ Необходимое условие экстремума:
- 47. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
- 48. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
- 49. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ В состоянии равновесия скорость реакции W равна 0:
- 50. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
- 51. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ Получаем связь равновесной и оптимальной температур проведения реакции:
- 52. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ откуда:
- 53. ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ После логарифмирования получаем:
- 55. Скачать презентацию




































 Возведение в степень произведения и степени
Возведение в степень произведения и степени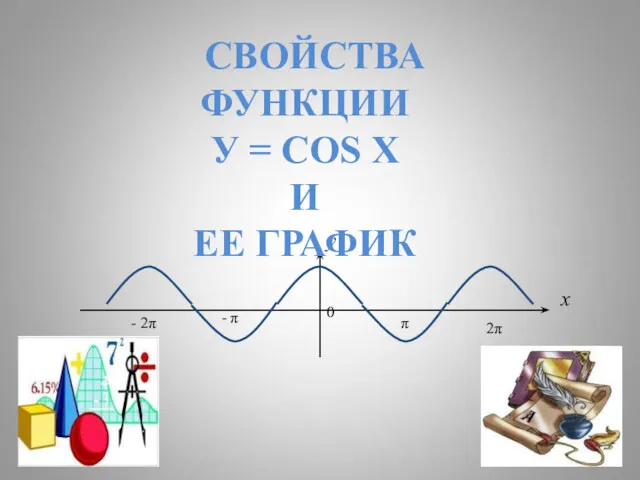 Свойства функции y=cos-x и ее график
Свойства функции y=cos-x и ее график Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3
Елементи теорії виміру. Шкали виміру. Лекція 6. Тема 3 Закрепление + - 3. Сравнение отрезков. 1 класс Школа России
Закрепление + - 3. Сравнение отрезков. 1 класс Школа России Степени и корни. Свойства степеней
Степени и корни. Свойства степеней Софья Ковалевская
Софья Ковалевская Числа 1 - 4
Числа 1 - 4 Метрология. Введение. Структура дисциплины
Метрология. Введение. Структура дисциплины grafy1
grafy1 Число и цифра 4.
Число и цифра 4. Тренажёр умножения на 2
Тренажёр умножения на 2 Статистическое распределение выборки и его основные числовые характеристики
Статистическое распределение выборки и его основные числовые характеристики Раскрытие скобок
Раскрытие скобок Медиа-сопровождение к уроку математики Число 9. Цифра 9
Медиа-сопровождение к уроку математики Число 9. Цифра 9 Урок математики для 2 класса Трёхзначные числа
Урок математики для 2 класса Трёхзначные числа НОД по математическому развитию в подготовительной группе.
НОД по математическому развитию в подготовительной группе. Решение обыкновенных дифференциальных уравнений (краевая задача)
Решение обыкновенных дифференциальных уравнений (краевая задача) Раскрытие скобок
Раскрытие скобок Цікаві факти з історії геометрії
Цікаві факти з історії геометрії Grafika komputerowa
Grafika komputerowa Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Формула пути. Решение задач на движение
Формула пути. Решение задач на движение Тест по теме: Тетраэдр и параллелепипед. Теория
Тест по теме: Тетраэдр и параллелепипед. Теория Система подготовки к ЕГЭ
Система подготовки к ЕГЭ Марковские системы массового обслуживания
Марковские системы массового обслуживания Логарифмы вокруг нас. История логарифмов
Логарифмы вокруг нас. История логарифмов Три точки зрения на геометрию вселенной
Три точки зрения на геометрию вселенной Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс
Презентация к уроку математики на тему: Случаи сложения вида 26+4. Переход через разряд 2 класс