Содержание
- 2. 2.1. БУЛЕВА АЛГЕБРА И ЕЕ ПРИМЕНЕНИЕ 2.1.1. Определение булевой алгебры
- 3. Название этого раздела математики связано с именем его основателя – Джорджа Буля. БУЛЬ (Boole) Джон английский
- 4. Используя классическое понятие алгебры, булеву алгебру можно определить как систему А=(В,φ1,φ2,…, φn), в которой несущим множеством
- 5. Основные логические операции, - дизъюнкция, конъюнкция и отрицание, - можно интерпретировать как операции, введенные в теории
- 6. Как правило, существует логическая интерпретация элементов множества В: 1 – истинно; 0 – ложно. В ряде
- 7. 2.1.2. Области применения булевой алгебры
- 8. Булева алгебра применяется: 1) как средство алгоритмического описания в языках программирования для определения логических условий; 2)
- 9. Алгебра логики позволяет производить анализ и синтез логических устройств. Анализ – это поиск аналитического выражения, которое
- 10. 2.1.3. Высказывания
- 11. Одним из базовых понятий в булевой алгебре является понятие высказывания. Высказывание – это любое повествовательное предложение,
- 12. Пример. Рассмотрим справедливость утверждений: а) число 4 – четное; b) снег – красный; с) 2*2=5. Значения
- 13. Два высказывания A и B называются эквивалентными, если их значения истинности совпадают. Значение истинности может быть
- 14. 2.2. ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- 15. 2.2.1. Понятие функции и способы ее задания
- 16. Пусть имеется n двоичных переменных x1, x2, …, xn. Каждая из них в некотором конкретном случае
- 17. Функция f, задающая однозначное отображение множества всевозможных наборов значений двоичных переменных x1, x2, …, xn во
- 18. Способы задания функции. Логическая функция может быть задана: 1) математическим выражением (формулой); 2) таблицей. Таблица является
- 20. Оценим число возможных наборов (число строк входных переменных). Конкретный набор – это вектор значений Количество наборов
- 21. Оценим возможное количество вариантов логических функций от n переменных. Множество вариантов логической функции можно представить как
- 22. Наборы, на которых функция равна единице, называют единичными наборами, а наборы, на которых функция равна нулю,
- 23. Две булевы функции и называют равными, если для всех возможных наборов значений аргументов они принимают одинаковые
- 24. Говорят, что булева функция Существенно зависит от аргумента xi , если , хотя бы для одного
- 25. 2.2.2. Элементарные логические операции
- 26. Из множества логических функций выделяется ряд наиболее простых операций, которые имеют ясную логическую интерпретацию: 1) отрицание
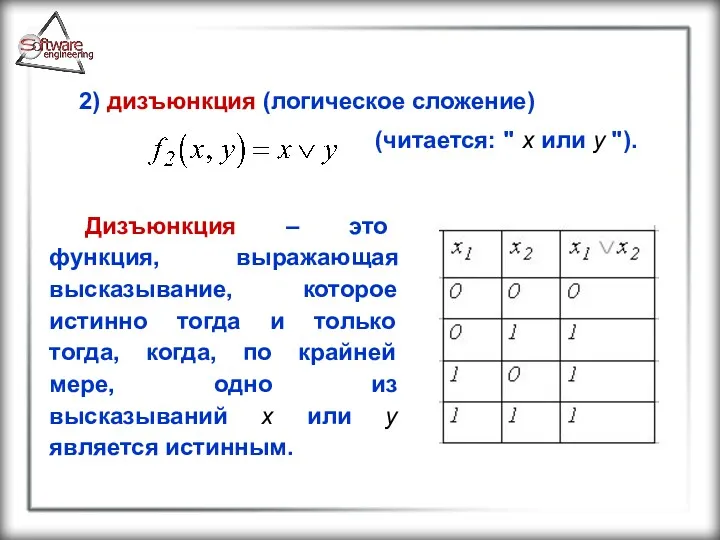
- 27. 2) дизъюнкция (логическое сложение) (читается: " x или y "). Дизъюнкция – это функция, выражающая высказывание,
- 28. 3) конъюнкция (логическое умножение) (читается: " x и y"). Для этой операции применяются также следующие формы
- 29. 4) импликация (читается : “если x, то y”). Функция f4 принимает значение ложно только тогда, когда
- 30. 5) эквивалентность (равнозначность) (читается: “x равно y ”). Функция f5=1 тогда и только тогда, когда значения
- 31. 6) сложение по модулю два (неравнозначность) Функция f6 истинна тогда и только тогда, когда значения аргументов
- 32. 7) штрих Шеффера Операция обратная по отношению к конъюнкции (функция ложна, только если оба аргумента истинны)
- 33. 8) стрелка Пирса Функция f8 обратная к дизъюнкции (f8 истинно, только когда x и y ложны)
- 35. Скачать презентацию































 Великая теорема Ферма
Великая теорема Ферма Элементы теории нечетких множеств
Элементы теории нечетких множеств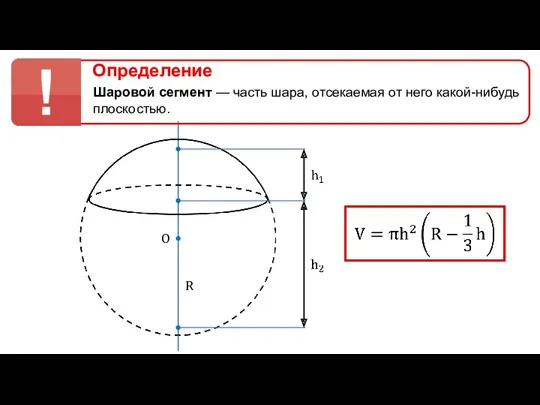 Объем частей шара
Объем частей шара Сложение отрицательных чисел» (фрагмент) для учащихся 6 класса
Сложение отрицательных чисел» (фрагмент) для учащихся 6 класса презентация по ФЕМП Первые шаги в математику
презентация по ФЕМП Первые шаги в математику Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Тригонометрические неравенства
Тригонометрические неравенства Математика 3 класс Виды треугольников.Треугольники в архитектуре.
Математика 3 класс Виды треугольников.Треугольники в архитектуре. Аксиомы стереометрии. (10 класс)
Аксиомы стереометрии. (10 класс) Ряды Фурье. Семинар 30
Ряды Фурье. Семинар 30 Координати та вектори в просторі
Координати та вектори в просторі Презентация к уроку математики в 1 классе Присчитывание и отсчитывание по1
Презентация к уроку математики в 1 классе Присчитывание и отсчитывание по1 Урок математики по теме: Умножение и деление на 3.
Урок математики по теме: Умножение и деление на 3. Квадратный корень из степени. Упражнение 9
Квадратный корень из степени. Упражнение 9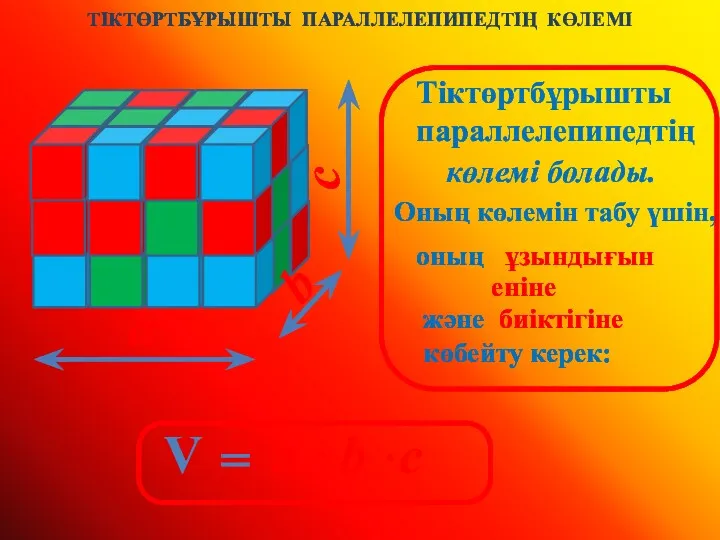 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Презентация по теме: Числа от 1 до 10
Презентация по теме: Числа от 1 до 10 Одночлен и его стандартный вид
Одночлен и его стандартный вид Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20
Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20 Конус. Виды конусов
Конус. Виды конусов Красота в математике или применение векторов к доказательству стереометрических теорем
Красота в математике или применение векторов к доказательству стереометрических теорем Теорема Пифагора – её история и значение
Теорема Пифагора – её история и значение Решение задач на концентрацию, смеси и сплавы
Решение задач на концентрацию, смеси и сплавы Введение в математический анализ и дифференциальное исчисление
Введение в математический анализ и дифференциальное исчисление Электронный справочник по тригонометрическим формулам
Электронный справочник по тригонометрическим формулам Доли. Обыкновенные дроби (математика, 5 класс)
Доли. Обыкновенные дроби (математика, 5 класс) День открытых дверей в 1 классе
День открытых дверей в 1 классе Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Сложение и вычитание десятичных дробей. Решение задач
Сложение и вычитание десятичных дробей. Решение задач