Слайд 2

Дискретная СВ Х, принимающая неотрицательные целочисленные значения, - 0,1,2,…, n называется
распределенной по биномиальному закону, если она принимает указанное значение m с вероятностью
Pm,n=P(X=m)=
По схеме Бернулли СВ Х есть число появлений события А ровно m раз в серии n опытов.
Слайд 3

Вероятность появления события А равна р, а непоявления q=(1-p).
ФР F(x) биномиального
закона распределения (БЗР) СВ Х имеет вид
Слайд 4

Для вычисления числовых характеристик этого распределения нам потребуется два вспомогательных равенства:
Слайд 5
![Определим числовые характеристики БЗР. Принимая во внимание первое вспомогательное равенство определим МО: M[X]=mx=](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-4.jpg)
Определим числовые характеристики БЗР. Принимая во внимание первое вспомогательное равенство определим
МО:
M[X]=mx=
Слайд 6
![С учетом второго вспомогательного равенства определим дисперсию: D[X]=α2[X] - mx](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-5.jpg)
С учетом второго вспомогательного равенства определим дисперсию:
D[X]=α2[X] - mx =
=
Величины n, p называются параметрами распределения.
Слайд 7

Пример: Устройство состоит из трех независимо работающих элементов. Вероятность отказа каждого
элемента в одном опыте равна 0,1. Составить закон распределения числа отказавших элементов в одном опыте.
Решение: Х - число отказавших элементов в одном опыте; х1 = 0 (ни один из элементов не отказал); х2 = 1 (отказал один элемент); х3 = 2 (отказали два элемента); х4 = 3 (отказали три элемента); n = 3; р = 0,1, следовательно, q = 1 - 0,1 = 0,9
Слайд 8

Р3,0 = q3 = 0,93 = 0,729;
Р3,1 = С13 р q2
=3 0,1 0,92 = 0,243;
Р3,2 = С23 р2 q = 3 0,12 0,9 = 0,027;
Р3,3 = р3 = 0,13 = 0,001.
Контроль: 0,729 + 0,243 + 0,027 + 0,001 = 1.
Искомый биномиальный закон распределения Х:
X 0 1 2 3
p 0,729 0,243 0,027 0,001
Слайд 9

§3.6.1.2. Распределение Пуассона
Теорема Пуассона. Если р→0 при n→∞, а np=λ, λ=const,
то СВ может принимать целые неотрицательные значения с вероятностями
Слайд 10

Для доказательства теоремы воспользуемся формулой Бернулли. Т.к. np=λ, p=λ/n и р→0
при n→∞, то
Слайд 11

Использовались соотношения:
Слайд 12

Т.о., дискретная СВ, принимающая целые неотрицательные значения 0, 1, 2,…, m
с вероятностью
называется распределенной по закону Пуассона.
Слайд 13

Ряд распределения этой СВ имеет вид:
X 0 1 2 … m
P …
Используя соотношение,
получим, что
Слайд 14
![Числовые характеристики этого закона: M[X]= и покажем, что дисперсия распределения Пуассона тоже равна λ.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-13.jpg)
Числовые характеристики этого закона:
M[X]=
и покажем, что дисперсия распределения Пуассона
тоже равна λ.
Слайд 15
![Принимая во внимание, что D[X]=α2[X] – (M[X])2, вычислим сначала второй начальный момент: α2[X]=](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-14.jpg)
Принимая во внимание, что
D[X]=α2[X] – (M[X])2, вычислим сначала второй начальный
момент:
α2[X]=
Слайд 16
![Т.о., D[X]=α2[X] – (M[X])2 =λ(λ+1)- λ2=λ. Величина λ называется параметром](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-15.jpg)
Т.о., D[X]=α2[X] – (M[X])2 =λ(λ+1)- λ2=λ.
Величина λ называется параметром распределения.
Вид
распределения Пуассона изменяется при различных значениях параметра распределения λ. При малых значениях λ наблюдается асимметрия закона распределения. С ростом λ имеется тенденция к симметрии.
Слайд 17

Пример: Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован
неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение: n=100000, p=0,0001, m=5.
Определим λ: λ=np=100000 ⋅ 0,0001=10
Искомая вероятность
P100000(5)=105e-10/5!=0,0378
Слайд 18

§3.6.2.Основные законы распределения непрерывных случайных величин
§3.6.2.1. Равномерное распределение
Слайд 19
![Непрерывная СВ называется равномерно распределенной на интервале [a, b], если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-18.jpg)
Непрерывная СВ называется равномерно распределенной на интервале [a, b], если плотность
ее распределения имеет постоянное значение С.
р(х)=
Определим C=const из условия нормировки
Слайд 20
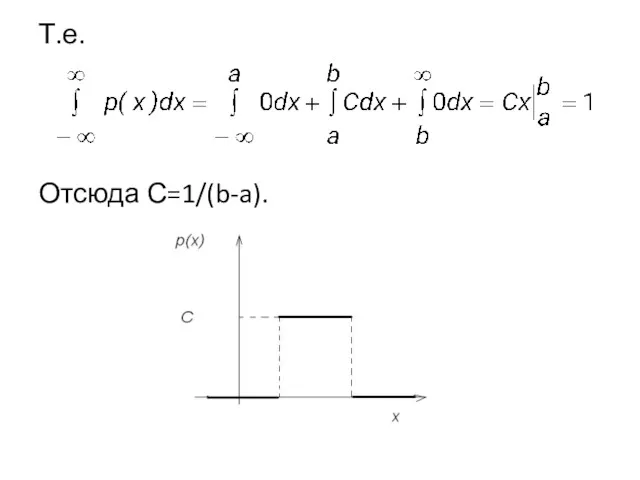
Слайд 21
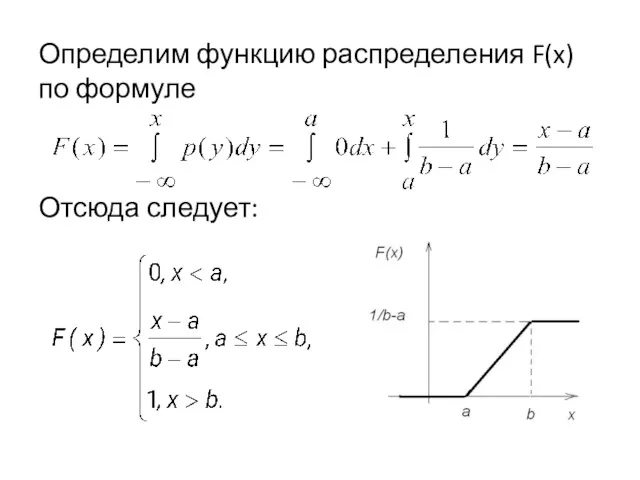
Определим функцию распределения F(x) по формуле
Отсюда следует:
Слайд 22
![Определим числовые характеристики распределения M[X], D[X]: Отсюда следует, что МО](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-21.jpg)
Определим числовые характеристики распределения M[X], D[X]:
Отсюда следует, что МО совпадает
с медианой. Определим дисперсию по формуле
D[X]=α2[X]–(M[X])2
Слайд 23
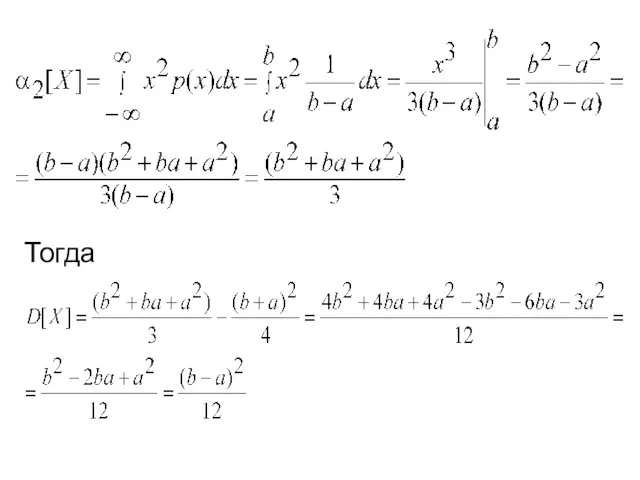
Тогда
Слайд 24

Стандартное отклонение определяется по формуле:
Равномерное распределение используется в технических приложениях,
когда информация о характеристиках распределения мала.
Слайд 25

Пример: Цена деления шкалы амперметра равна 0,1А. Показания округляют до ближайшего
целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02А.
Решение: Ошибка округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения ƒ(х)=1/(b-a), где (b-a) – длина интервала, в котором заключены возможные значения Х; вне этого интервала ƒ(х)=0.



![Определим числовые характеристики БЗР. Принимая во внимание первое вспомогательное равенство определим МО: M[X]=mx=](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-4.jpg)
![С учетом второго вспомогательного равенства определим дисперсию: D[X]=α2[X] - mx](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-5.jpg)







![Числовые характеристики этого закона: M[X]= и покажем, что дисперсия распределения Пуассона тоже равна λ.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-13.jpg)
![Принимая во внимание, что D[X]=α2[X] – (M[X])2, вычислим сначала второй начальный момент: α2[X]=](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-14.jpg)
![Т.о., D[X]=α2[X] – (M[X])2 =λ(λ+1)- λ2=λ. Величина λ называется параметром](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-15.jpg)


![Непрерывная СВ называется равномерно распределенной на интервале [a, b], если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-18.jpg)


![Определим числовые характеристики распределения M[X], D[X]: Отсюда следует, что МО](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/119017/slide-21.jpg)


 Круглые тела
Круглые тела Алгоритм построения графика квадратичной функции
Алгоритм построения графика квадратичной функции Окружность. Отличие круга от окружности
Окружность. Отличие круга от окружности Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Умножение. 2 класс.
Умножение. 2 класс. Линейные векторные пространства. Базис
Линейные векторные пространства. Базис ЗНАКОМСТВО ДОШКОЛЬНИКОВ С ПОНЯТИЕМ ЧИСЛО
ЗНАКОМСТВО ДОШКОЛЬНИКОВ С ПОНЯТИЕМ ЧИСЛО Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области. Лeкция №6-7
Экстремум функции нескольких переменных. Наибольшее и наименьшее значения функции в замкнутой области. Лeкция №6-7 Квадратичная функция, её свойства и график
Квадратичная функция, её свойства и график Вычеты. Основная теорема о вычетах
Вычеты. Основная теорема о вычетах Решение уравнений. Алгоритм решения уравнений
Решение уравнений. Алгоритм решения уравнений Умножение. Переместительное свойство умножения. Закрепление. Математика. 5 класс
Умножение. Переместительное свойство умножения. Закрепление. Математика. 5 класс устная работа на уроках математики в 5 классе
устная работа на уроках математики в 5 классе Построение сечений
Построение сечений Решение задач с помощью уравнений. 6 класс
Решение задач с помощью уравнений. 6 класс Перпендикулярність площин
Перпендикулярність площин Табличное сложение (1 класс)
Табличное сложение (1 класс) В гости к Бабе Яге Счёт до 10
В гости к Бабе Яге Счёт до 10 Формула Грина. Поверхностные интегралы
Формула Грина. Поверхностные интегралы Интегрированный урок математики и окружающего мира в 3 классе Письменное сложение и вычитание трёхзначных чисел( презентация )
Интегрированный урок математики и окружающего мира в 3 классе Письменное сложение и вычитание трёхзначных чисел( презентация ) Кроссворды по математике
Кроссворды по математике Развитие приемов умственной деятельности. Прием сравнения
Развитие приемов умственной деятельности. Прием сравнения свойства величин
свойства величин Визначник другого та третього порядків
Визначник другого та третього порядків Похибки наближених обчислень
Похибки наближених обчислень Подготовка к ЕГЭ (профильный уровень). Задания 4
Подготовка к ЕГЭ (профильный уровень). Задания 4 Окружность и ее элементы. Замечательные линии окружности
Окружность и ее элементы. Замечательные линии окружности Конспект урока и презентация по теме Сложение и вычитание величин
Конспект урока и презентация по теме Сложение и вычитание величин