Содержание
- 2. ПЛАН ЛЕКЦИИ 1 ДИФФЕРЕНЦИРОВАНИЕ 1.1 Определение производной, правила дифференцирования. 1.2 Механический и геометрический смысл производной. 1.3
- 3. 1.1 Определение производной, правила дифференцирования. Производная – это предел отношения приращения функции к приращению ее аргумента
- 4. 3. (c u)/=c u/ Постоянное число можно выносить за знак производной. Пример: (7x)/=7x/=7*1=7. 4. (u +v-w+…+s)/=u/+v/-w/+…+s/.
- 5. ( )/ = = 7. (sin u)/=u/cosu. Производная синуса сложной функции равна произведению производной этой сложной
- 6. (3x2*sinx)=(3x2)/*sinx+3x2 *(sinx)/ =6x*sinx+3x2*cosx, (sin5x*cos2x)/=(sin5x)/*cos2x+sin5x*(cos2x)/=5cos5x*cos2x-2sin2xsin5x. ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ Пусть дана функция y=f(g(x))=F(x) – сложная функция аргумента x.
- 7. ФОРМУЛЫ ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ (U + V)/= U/ + V/ 2. (U * V)/= U/ * V
- 8. И. Ньютон впервые сформулировал, что с позиции механики мгновенная скорость прямолинейно движущейся точки есть первая производная
- 9. В медицине и биологии, используя производную, можно определить скорость изменения различных параметров системы или процесса в
- 10. Задача: Составить уравнение нормали и касательной к данным кривым в точке с абсциссой x0. y =
- 11. Adx + q(dx), где A не зависит от dx, но зависит от x, то функция y=f(x)
- 12. Найти полный дифференциал следующей функции: U(x,y,z)=ln(x3+y2+z2). Решение dU(x,y,z)= 3x2/(x3+y2+z2)*dx+ 2y/(x3+y2+z2)*dy+ 2z/(x3+y2+z2)*dz 2.1 Первообразная и неопределенный интеграл,
- 13. Неопределённый интеграл представляет собой любую функцию, дифференциал которой равен подинтегральному выражению, производная равна подинтегральной функции. Таким
- 14. 2. Дифференциал неопределённого интеграла равен подынтыгральному выражению: 3. Неопределенный интеграл от производной функции отличается от самой
- 15. Основные формулы неопределённых интегралов
- 16. Пример: Непосредственное интегрирование Пример: Интегрирование разложением
- 17. 2.2 Методы интегрирования. Рассмотрим два метода интегрирования: МЕТОД ПОДСТАНОВКИ, МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ. Метод подстановки Наиболее
- 18. Пример: Найти интеграл Применим подстановку: u=arctg(x), тогда du=dx/1+x2 Подставляя полученные значения в искомый интеграл получим: Теперь
- 19. Метод интегрирования по частям Из дифференциального исчисления известно, что если u и v – дифференцируемые функции
- 20. Пример: Найти интеграл Положим u = x, dv = sin(x)dx, тогда du = dx, v =
- 21. Данное равенство называется формулой Ньютона – Лейбница. Предполагается при этом, что подынтегральная функция f(x) непрерывна при
- 22. Пример: Найти определённый интеграл Решение
- 23. 3.1 Определение дифференциальных уравнений. Дифференциальные уравнения с частными производными. Дифференциальным уравнением – называют уравнение, связывающее независимую
- 25. Скачать презентацию






















 Числа и вычисления (6 класс)
Числа и вычисления (6 класс) Введение в математический анализ
Введение в математический анализ Архитектура и математика
Архитектура и математика Логические задачи-шутки на уроках математики в первом классе
Логические задачи-шутки на уроках математики в первом классе Играем с Машей и медведем
Играем с Машей и медведем Игра Кто хочет стать математиком
Игра Кто хочет стать математиком Сводка и группировка статистических данных. Тема 3
Сводка и группировка статистических данных. Тема 3 Устный счет
Устный счет Математическая раскраска Бабочка
Математическая раскраска Бабочка Мастер класс. Работа с задачами на движение.
Мастер класс. Работа с задачами на движение. Задачи на построение
Задачи на построение Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Геометрическое тело цилиндр
Геометрическое тело цилиндр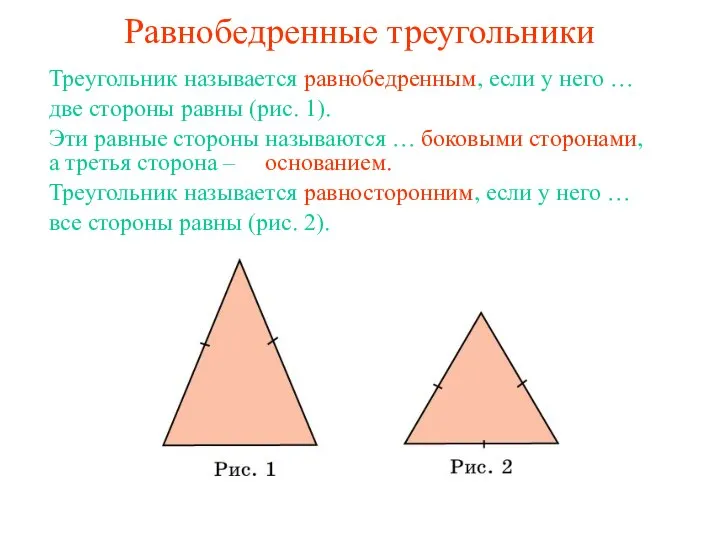 Равнобедренные треугольники
Равнобедренные треугольники Математическое моделирование в различных областях знания
Математическое моделирование в различных областях знания Построение графика квадратичной функции
Построение графика квадратичной функции Применение ФСУ. Алгебра. 7 класса
Применение ФСУ. Алгебра. 7 класса Алгоритм умножения на трёхзначное число
Алгоритм умножения на трёхзначное число Обучение детей математике с использованием художественных произведений: Величина-2
Обучение детей математике с использованием художественных произведений: Величина-2 Периметр квадрата и прямоугольника. Презентация.
Периметр квадрата и прямоугольника. Презентация. Геометрические построения
Геометрические построения Математика. Устный счёт
Математика. Устный счёт Площадь многоугольника. Свойства площадей
Площадь многоугольника. Свойства площадей Russian mathematician. Sofia Kovalevskaya
Russian mathematician. Sofia Kovalevskaya Электронный тест по математике для 1 класса по теме Сложение и вычитание числа 5
Электронный тест по математике для 1 класса по теме Сложение и вычитание числа 5 Correlation and regression
Correlation and regression Производная в биологии
Производная в биологии Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников