Содержание
- 2. Подавляющее большинство социально-экономических решений приходится принимать с учетом противоречивых интересов, относящихся либо к различным лицам или
- 3. 1. Основные понятия теории матричных игр
- 4. Теория игр, раздел математики, изучающий формальные модели принятия оптимальных решений в условиях конфликта. Под конфликтом понимается
- 5. Отдельные математические вопросы, касающиеся конфликтов, рассматривались начиная с 17 в. многими учёными. Систематическая же математическая теория
- 6. В условиях конфликта стремление противника скрыть свои предстоящие действия порождает неопределённость. Наоборот, неопределённость при принятии решений
- 7. Всякая игра включает в себя три элемента: участников игры – игроков, правила игры, оценку результатов действий
- 8. Стратегией игрока называется совокупность правил, определяющих выбор варианта действий при каждом личном ходе в зависимости от
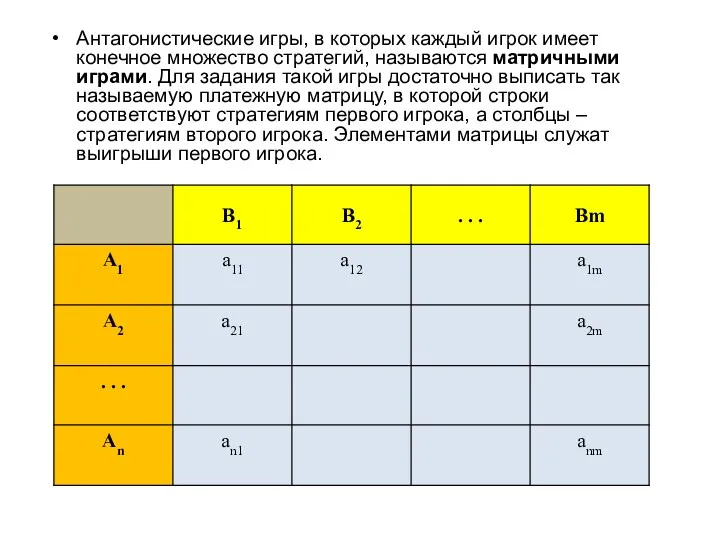
- 9. Антагонистические игры, в которых каждый игрок имеет конечное множество стратегий, называются матричными играми. Для задания такой
- 10. Рассмотрим простейшую модель – игру, в которой участвуют два игрока, множество стратегий каждого игрока конечно, а
- 11. Такую игру (Г ) называют матричной. Она определяется тройкой Г=(X,Y,K), где Х – множество стратегий 1-го
- 12. Пусть 1-й игрок имеет всего m стратегий, а 2-й – n стратегий: Х=М={1,2, …, m}, Y=N={1,2,
- 13. Принцип минимакса (максимина) Величина называется нижней ценой игры или максиминным выигрышем (максимином). Величина называется верхней ценой
- 14. Пусть – платежная матрица игры Г. Если 1-й игрок выбрал стратегию i, то в худшем случае
- 15. Второй игрок, выбрав стратегию j, в худшем случае проиграет , а значит, может гарантировать себе проигрыш
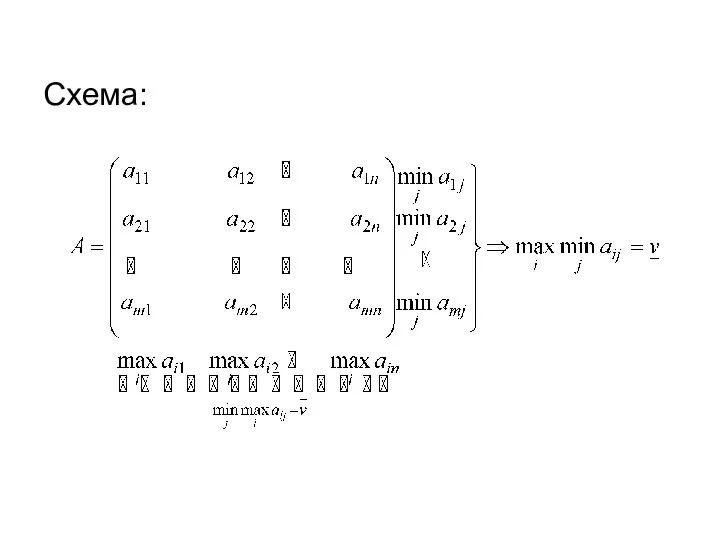
- 16. Схема:
- 17. Например, Соответствующие стратегии: i0=1(максиминная), j0=1,2 (минимаксная).
- 18. Справедливо неравенство:
- 19. Ситуация (i*, j*) называется ситуацией равновесия, или седловой точкой, если для любых , , выполняется неравенство
- 20. Ситуация равновесия существует тогда и только тогда, когда (это значение и является ценой игры v).
- 21. Например, (2,3)-ситуация равновесная, v =4 – цена игры, i*=2, j*=3 – оптимальные стратегии 1-го и 2-го
- 22. Смешанной стратегией для 1-го игрока называется упорядоченная система m действительных чисел x=(x1, x2, …, xm), ,
- 23. Функция выигрыша K(x,y) в ситуации (x,y) определяется как математическое ожидание выигрыша 1-го игрока при условии, что
- 24. Если для некоторых и и для всех и выполняется неравенство , то x*, y* называются оптимальными
- 25. Свойства оптимальных стратегий.
- 26. 1. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА с ценой v. Тогда, для того
- 27. 2. Пусть K(x,y) – математическое ожидание выигрыша в игре ГА, v – действительное число, , .
- 28. 3. Если x*, y* – решение -игры ГА, то
- 29. 4. Пусть , , v – решение игры ГА. Тогда для любого , при котором ,
- 30. 5. (Лемма о масштабе). Если ГА – игра с матрицей , а – игра с матрицей
- 31. 2. ( ) - игры
- 32. Пусть – платежная матрица игры Г. Если она не имеет седловой точки, то единственное решение игры
- 33. 1) решив две системы:
- 34. 2) по формулам: или или
- 35. 3) в матричном виде: где – определитель матрицы А, А* – присоединенная к А матрица (транспонированная
- 36. Найдем, например, решение игры с платежной матрицей , которая не имеет седловой точки.
- 37. 1) Составим системы: Решив системы, получим: то есть -решение игры.
- 38. 2) Найдем решение по формулам:
- 40. Скачать презентацию
























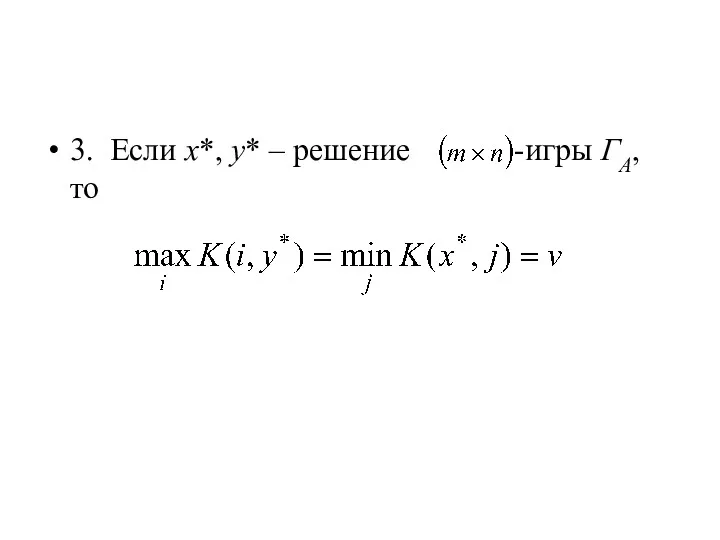





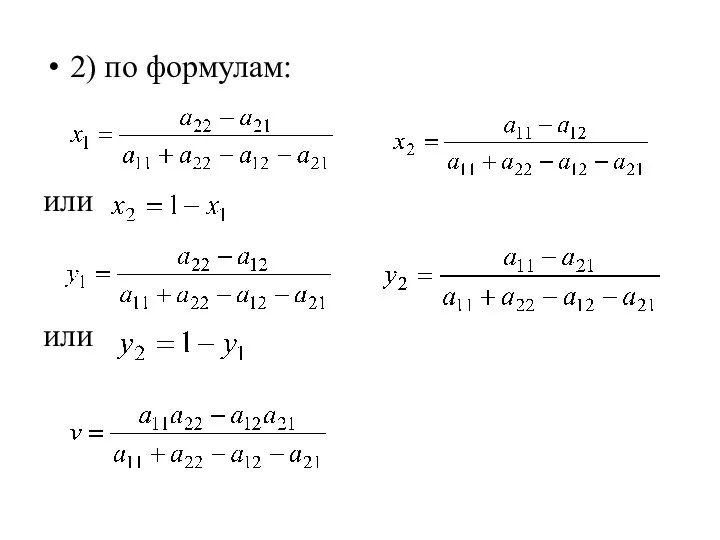




 Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс
Сложение и вычитание алгебраических дробей с разными знаменателями. 7 класс Элементы дисперсионного анализа
Элементы дисперсионного анализа Презентации по математике 1 класс Школа 2100
Презентации по математике 1 класс Школа 2100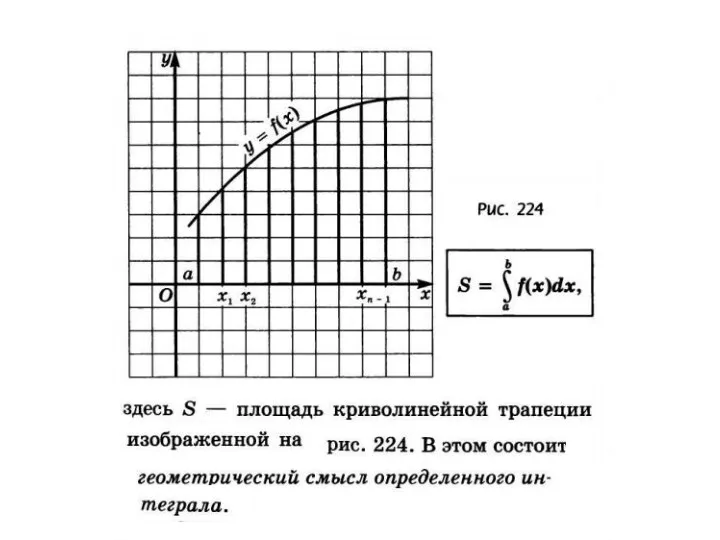 Применение интеграла
Применение интеграла Проект. Теорема Пифагора (вчера, сегодня, завтра…)
Проект. Теорема Пифагора (вчера, сегодня, завтра…) Порядок действий (устный счёт)
Порядок действий (устный счёт) Устный счёт Сложение трёхзначных чисел Диск
Устный счёт Сложение трёхзначных чисел Диск Математика для детей
Математика для детей Сложение и вычитание в пределах 10. Интерактивный тренажёр-раскраска
Сложение и вычитание в пределах 10. Интерактивный тренажёр-раскраска Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график Степень с натуральным показателем
Степень с натуральным показателем Степенные производные функции комплексных переменных
Степенные производные функции комплексных переменных Параллельный перенос графика функции
Параллельный перенос графика функции Арифметические действия. Двузначные числа (устные вычисления).
Арифметические действия. Двузначные числа (устные вычисления). Доли. Обыкновенные дроби. 5 класс
Доли. Обыкновенные дроби. 5 класс Степенева функція
Степенева функція Треугольники. Упражнение 13
Треугольники. Упражнение 13 Умножение одночленов
Умножение одночленов Конспект урока по математике во 2 классе
Конспект урока по математике во 2 классе Нахождение дроби от числа. Применение распределительного свойства умножения
Нахождение дроби от числа. Применение распределительного свойства умножения Математический язык
Математический язык Пределы и непрерывность
Пределы и непрерывность Тела вращения. Площади поверхности и объёмы
Тела вращения. Площади поверхности и объёмы Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов
Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов Формула суммы n первых членов геометрической прогрессии
Формула суммы n первых членов геометрической прогрессии Рациональные числа. Иррациональные числа
Рациональные числа. Иррациональные числа Делители и кратные. 6 класс
Делители и кратные. 6 класс Вычитание числа 2.
Вычитание числа 2.