Содержание
- 2. Стереометрия – это геометрия в пространстве. Нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы
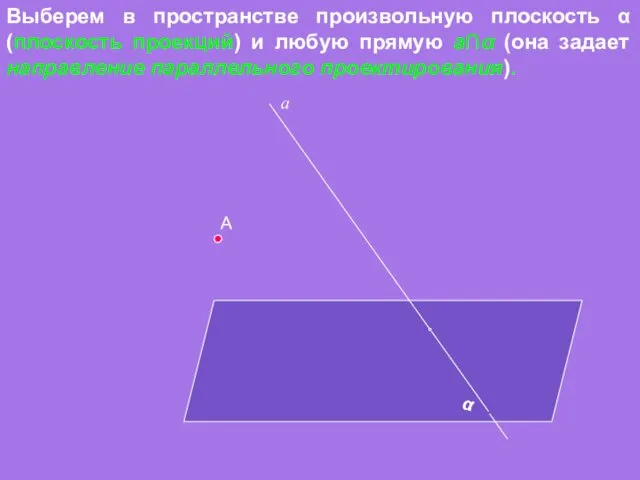
- 3. А Выберем в пространстве произвольную плоскость α (плоскость проекций) и любую прямую a∩α (она задает направление
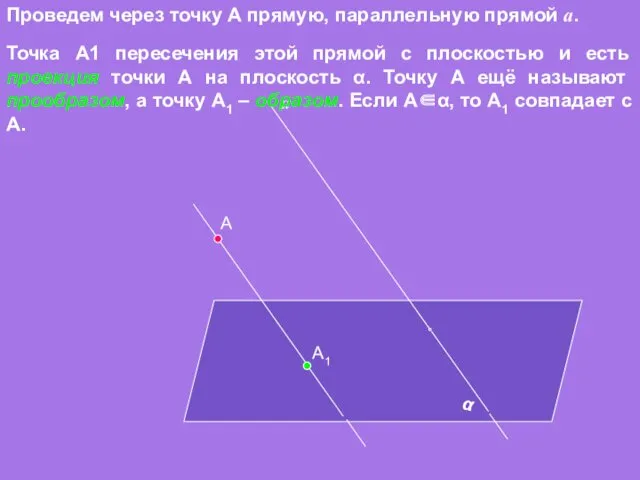
- 4. А α а Проведем через точку А прямую, параллельную прямой а. А1 Точка А1 пересечения этой
- 5. Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры. Таким
- 6. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции А а α
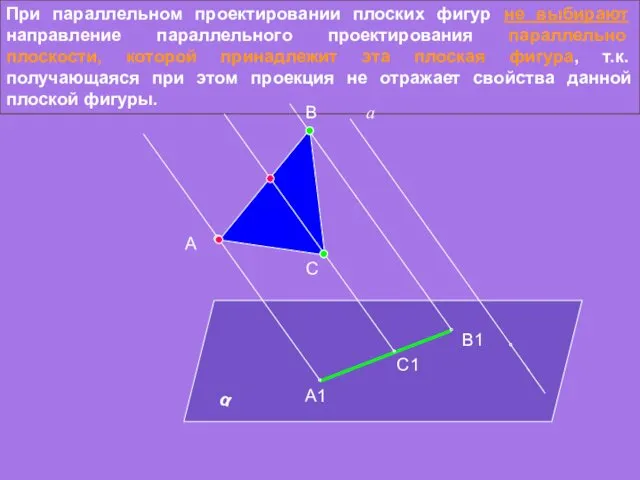
- 7. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская
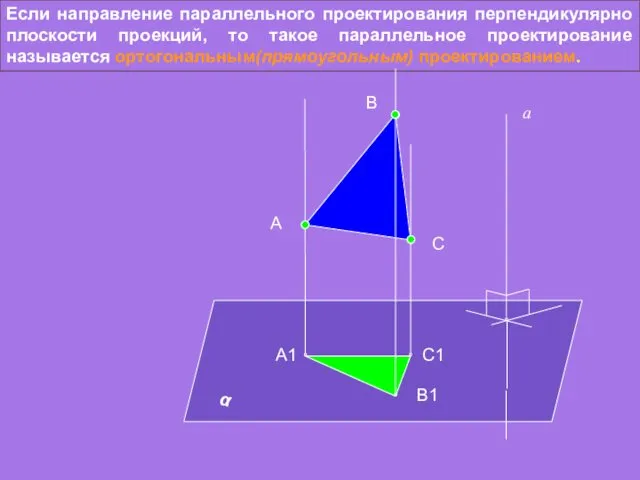
- 8. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным(прямоугольным) проектированием. А а
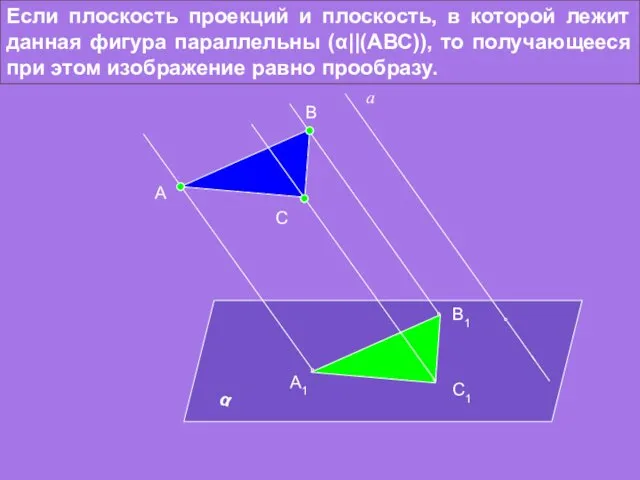
- 9. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны (α||(АВС)), то получающееся при этом
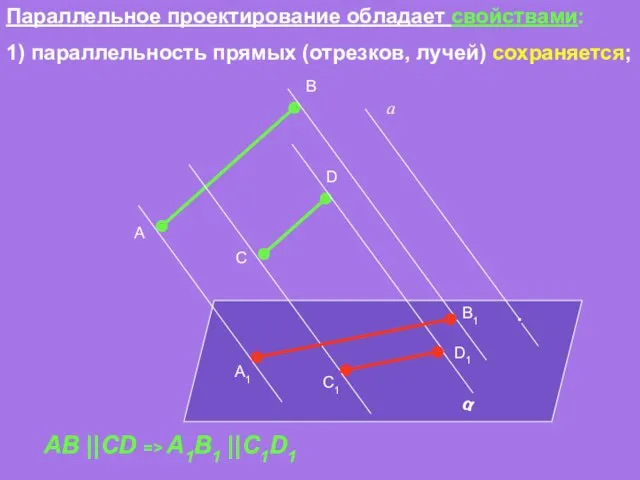
- 10. Параллельное проектирование обладает свойствами: 1) параллельность прямых (отрезков, лучей) сохраняется; α а A D C B
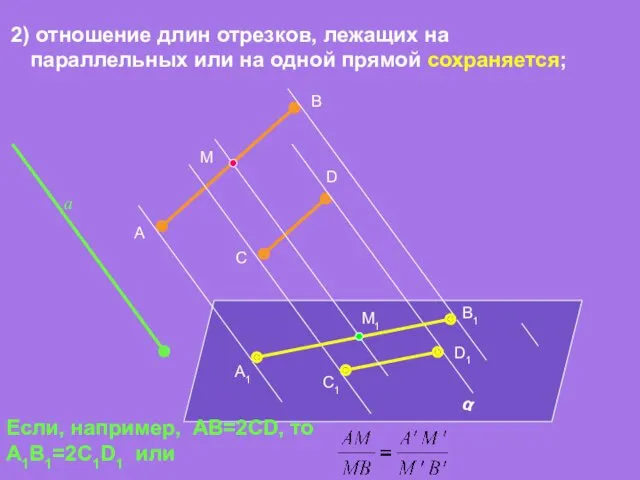
- 11. 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется; α а A D
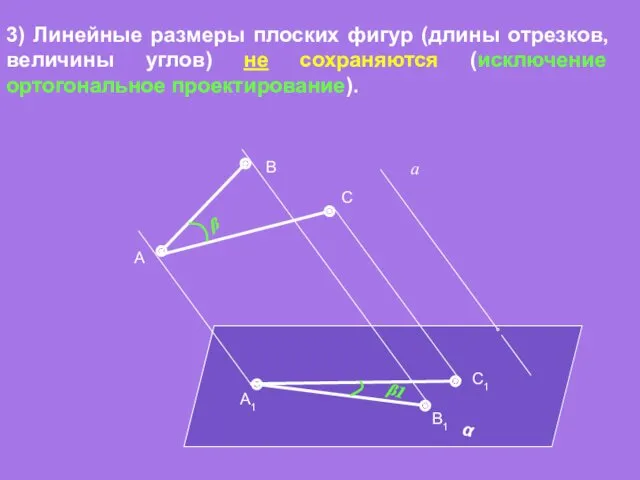
- 12. α а A B A1 B1 3) Линейные размеры плоских фигур (длины отрезков, величины углов) не
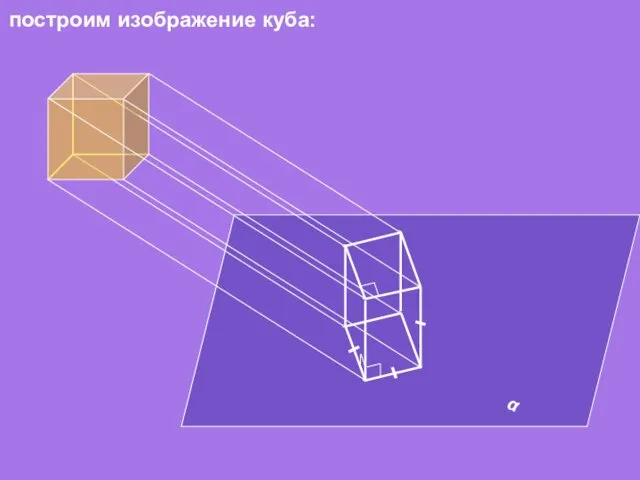
- 13. α построим изображение куба:
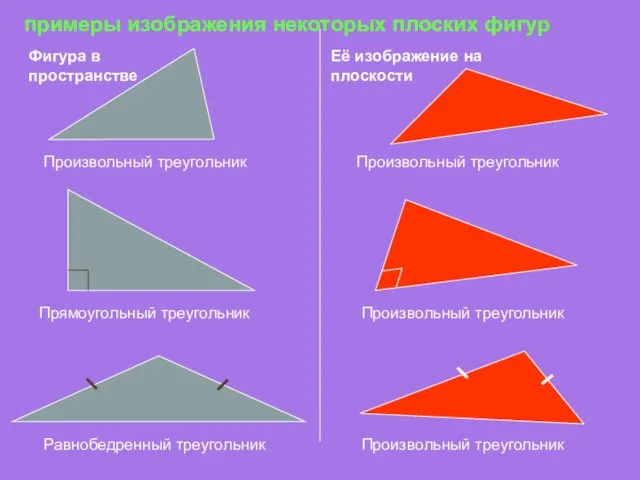
- 14. Фигура в пространстве Её изображение на плоскости Произвольный треугольник Произвольный треугольник Прямоугольный треугольник Произвольный треугольник Равнобедренный
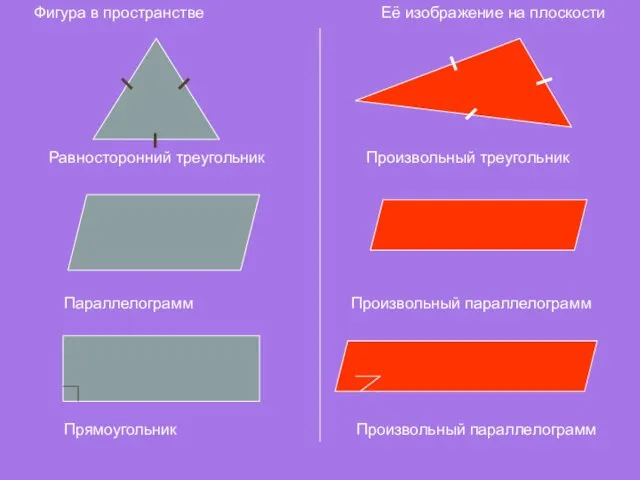
- 15. Фигура в пространстве Её изображение на плоскости Равносторонний треугольник Произвольный треугольник Параллелограмм Произвольный параллелограмм Прямоугольник Произвольный
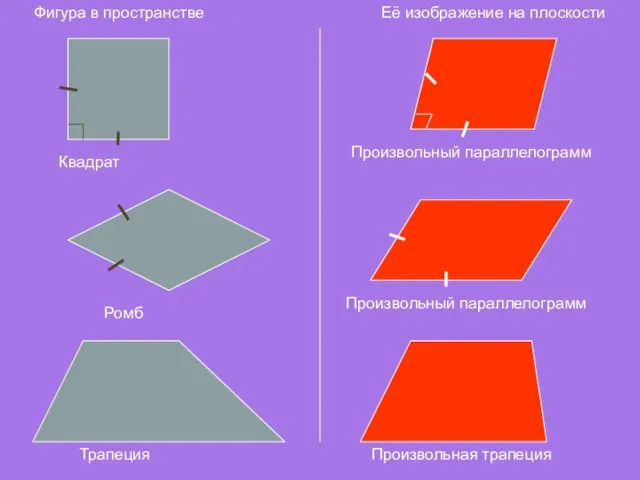
- 16. Фигура в пространстве Её изображение на плоскости Квадрат Произвольный параллелограмм Трапеция Произвольная трапеция Произвольный параллелограмм Ромб
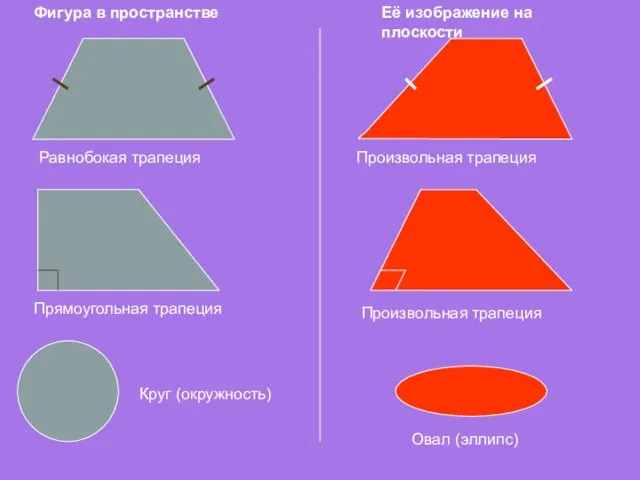
- 17. Фигура в пространстве Её изображение на плоскости Равнобокая трапеция Произвольная трапеция Прямоугольная трапеция Произвольная трапеция Круг
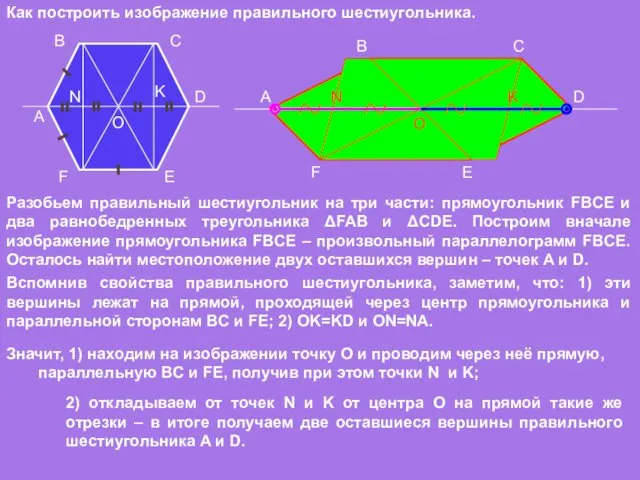
- 18. A B C D E F O Как построить изображение правильного шестиугольника. F A B C
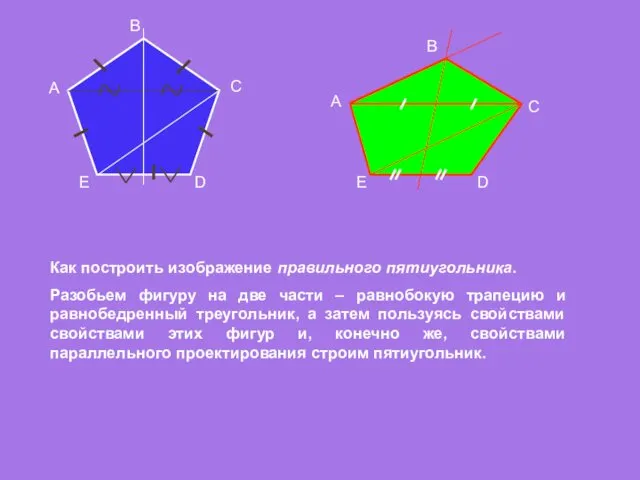
- 19. A B C D E Как построить изображение правильного пятиугольника. Разобьем фигуру на две части –
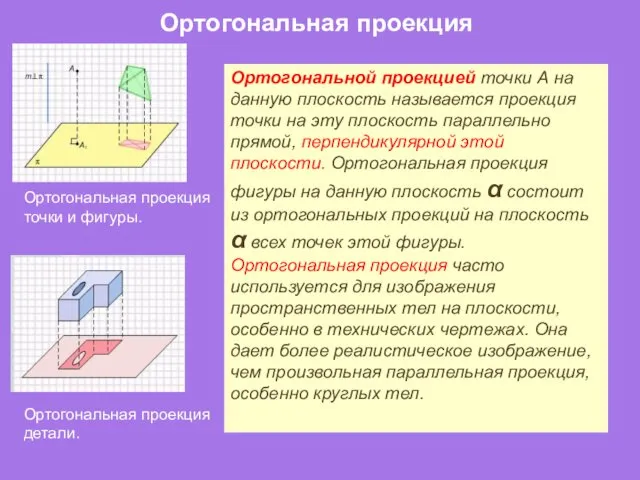
- 20. Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной
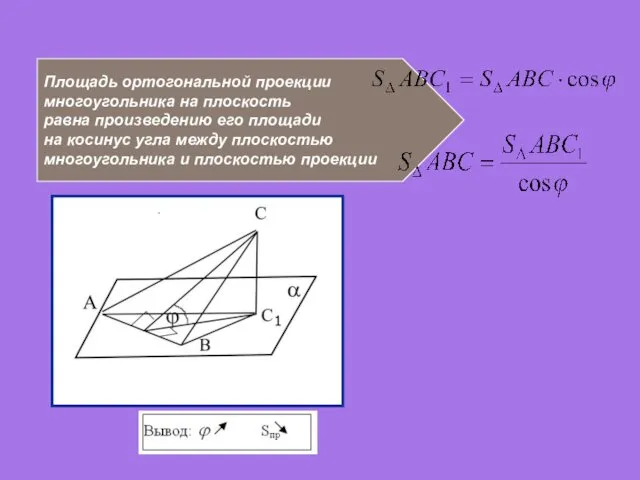
- 21. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника
- 22. Задача: Найти площадь ортогональной проекции равнобедренного треугольника на плоскость, если угол между плоскостью данного треугольника и
- 23. Измерение расстояний в пространстве
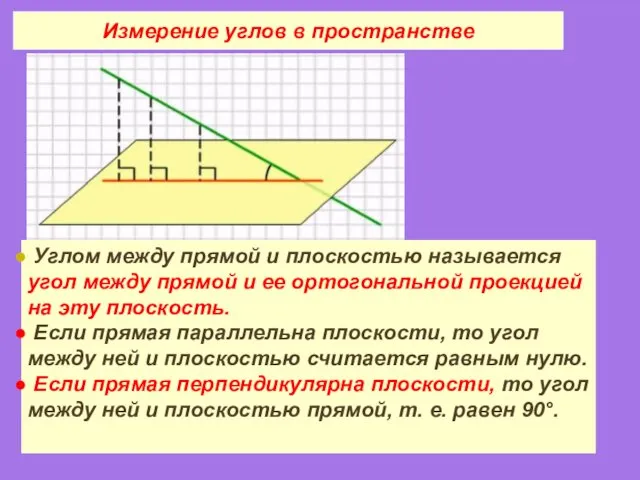
- 24. Измерение углов в пространстве Углом между прямой и плоскостью называется угол между прямой и ее ортогональной
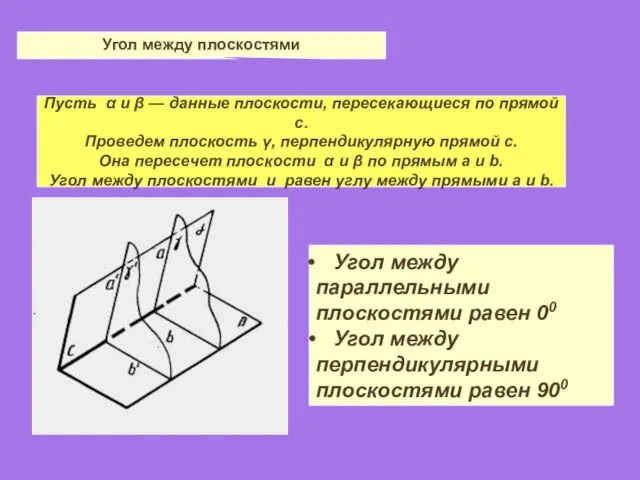
- 25. Пусть α и β — данные плоскости, пересекающиеся по прямой с. Проведем плоскость γ, перпендикулярную прямой
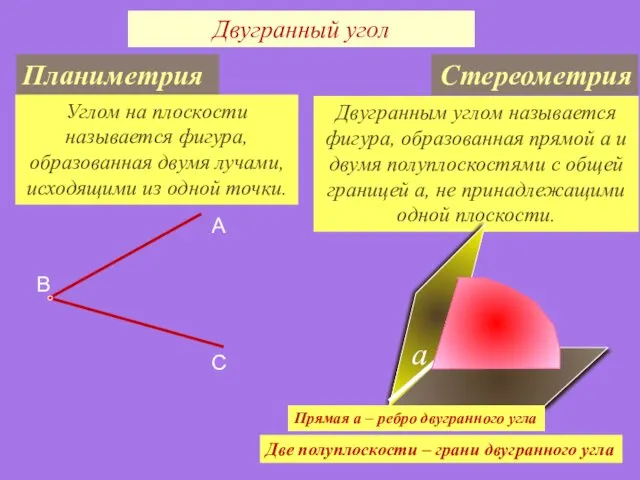
- 26. Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими
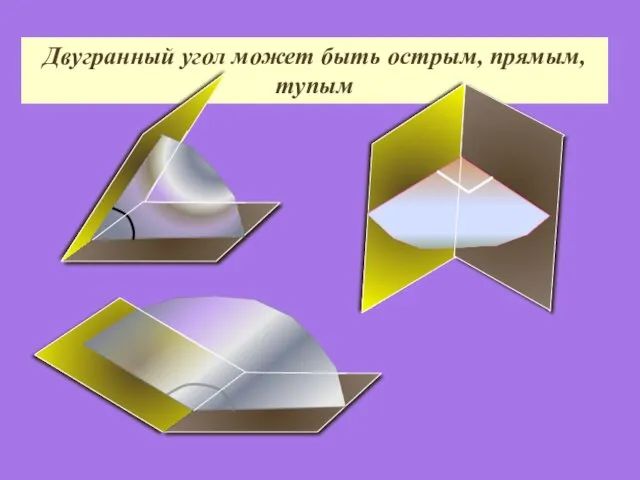
- 27. Двугранный угол может быть острым, прямым, тупым
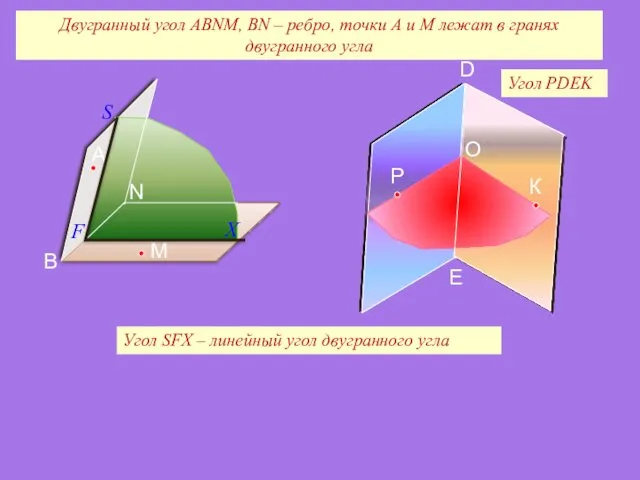
- 28. Угол РDEK Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях двугранного
- 29. Угол РОК – линейный угол двугранного угла РDEК. D E Градусной мерой двугранного угла РDEК называется
- 31. Скачать презентацию






 Аксонометрия
Аксонометрия Умножение многозначных чисел на двузначные
Умножение многозначных чисел на двузначные Параллельные прямые
Параллельные прямые Признаки параллельности прямых
Признаки параллельности прямых Вычитание рациональных чисел. 6 класс
Вычитание рациональных чисел. 6 класс Карл Фридрих Гаусс
Карл Фридрих Гаусс Задание 11: текстовые задачи
Задание 11: текстовые задачи Знакомство с числом 0 и цифрой 0.
Знакомство с числом 0 и цифрой 0. Размах и центральные тенденции. Во владениях королевы статистики
Размах и центральные тенденции. Во владениях королевы статистики Метод координат в пространстве. Координаты точки и координаты вектора
Метод координат в пространстве. Координаты точки и координаты вектора Урок математики в 1 классе Уменьшаемое. Вычитаемое. Разность
Урок математики в 1 классе Уменьшаемое. Вычитаемое. Разность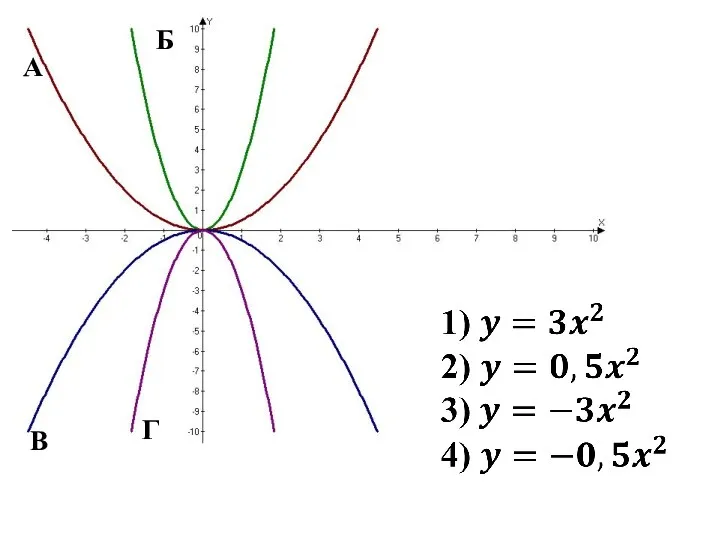 Парабола, гипербола
Парабола, гипербола Арифметическая прогрессия. Тест
Арифметическая прогрессия. Тест Округление чисел. Прикидки
Округление чисел. Прикидки Пропорции и проценты
Пропорции и проценты Сплавы, растворы, смеси
Сплавы, растворы, смеси ЕГЭ-ОГЭ. Математика
ЕГЭ-ОГЭ. Математика Устный счет Осенний листопад (презентация к уроку математики, 3 класс)
Устный счет Осенний листопад (презентация к уроку математики, 3 класс) Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Полуплоскость. Луч. Прямая
Полуплоскость. Луч. Прямая Метод рационализации. Решение задания №17. Подготовка к ЕГЭ 2019 по математике
Метод рационализации. Решение задания №17. Подготовка к ЕГЭ 2019 по математике Применение производной при исследовании функций
Применение производной при исследовании функций Дидактическая электронная игра
Дидактическая электронная игра Математический диктант
Математический диктант Координатна площина
Координатна площина Измерение углов. Транспортир
Измерение углов. Транспортир Презентация к уроку по математике
Презентация к уроку по математике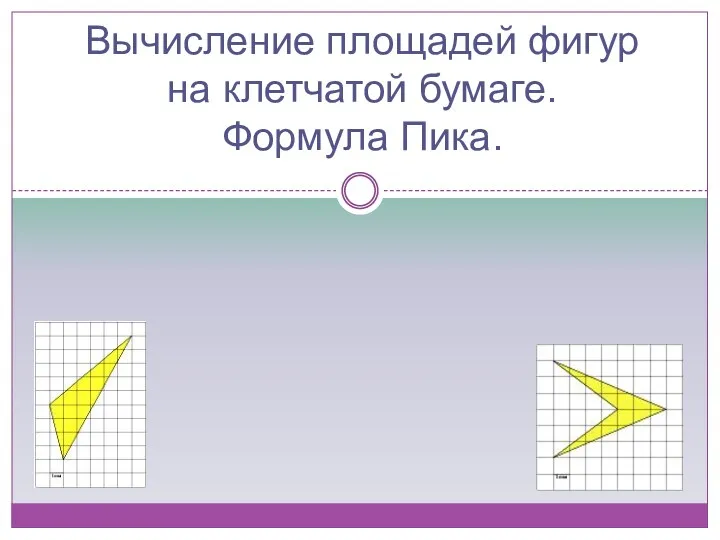 Вычисление площадей фигур на клетчатой бумаге. Формула Пика (8 класс)
Вычисление площадей фигур на клетчатой бумаге. Формула Пика (8 класс)