Содержание
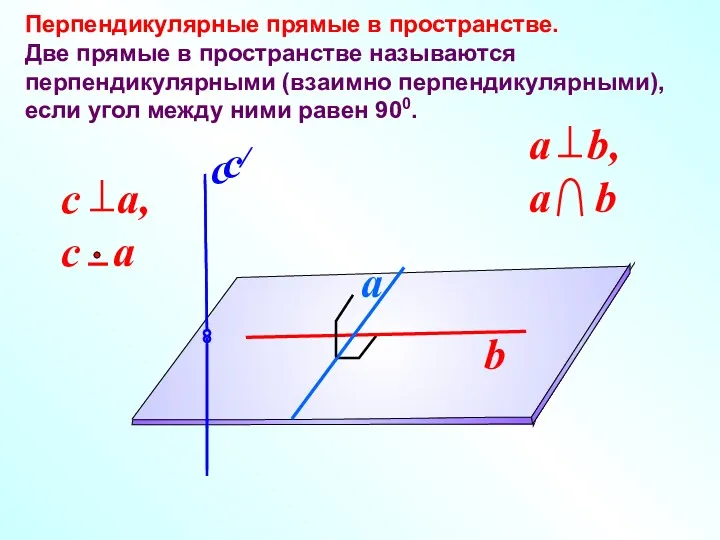
- 2. Перпендикулярные прямые в пространстве. Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними
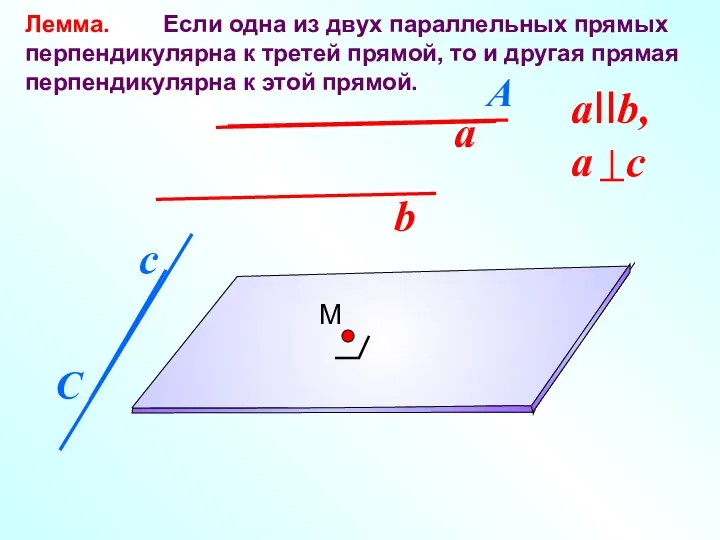
- 3. Лемма. Если одна из двух параллельных прямых перпендикулярна к третей прямой, то и другая прямая перпендикулярна
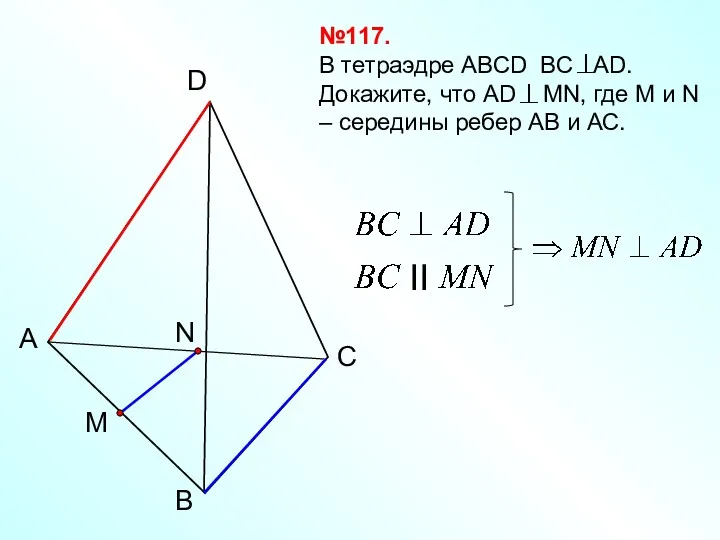
- 4. B А C D №117. В тетраэдре АВСD ВС АD. Докажите, что АD MN, где М
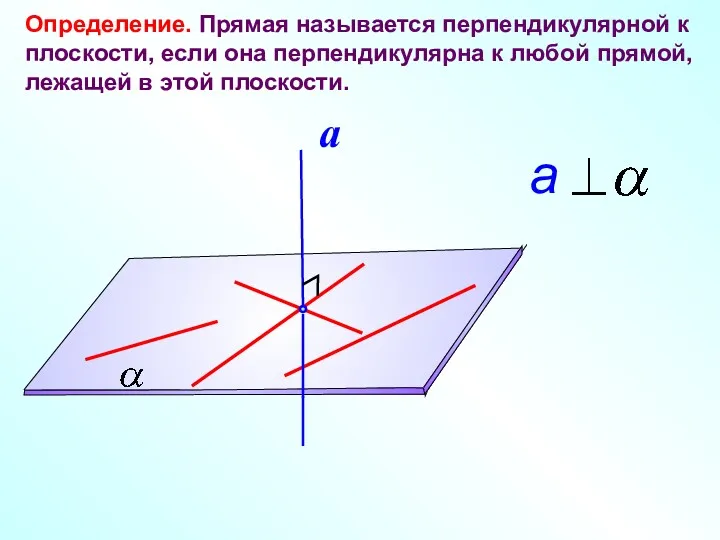
- 5. Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
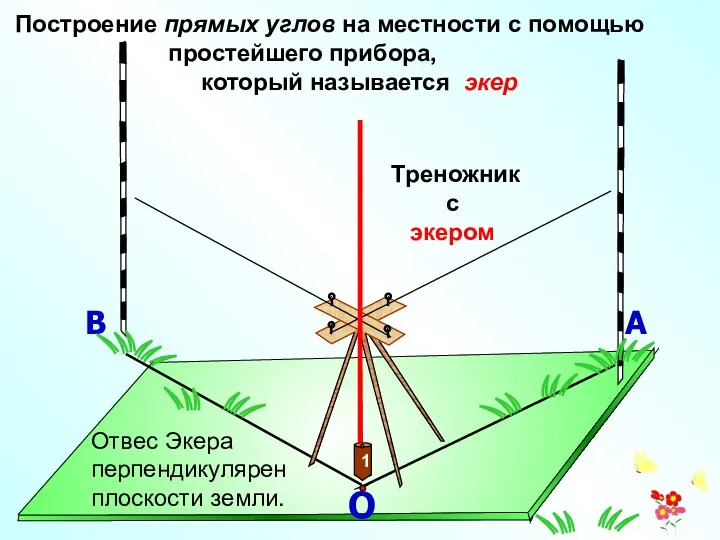
- 6. О А В Построение прямых углов на местности с помощью простейшего прибора, который называется экер Треножник
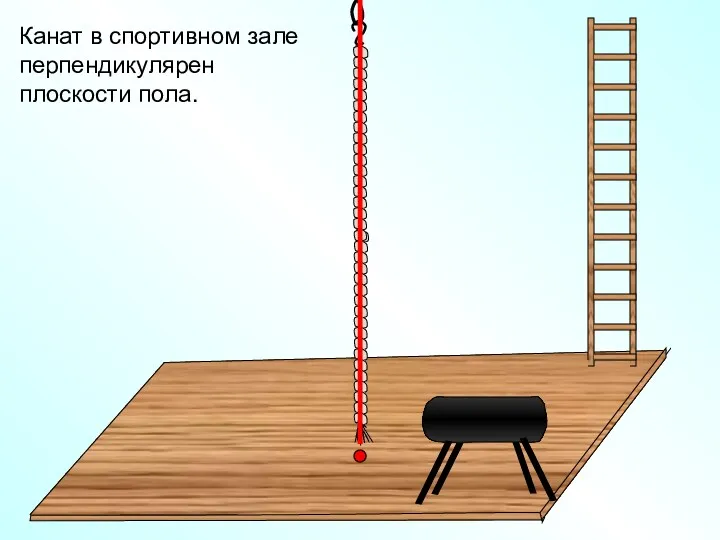
- 7. Канат в спортивном зале перпендикулярен плоскости пола.
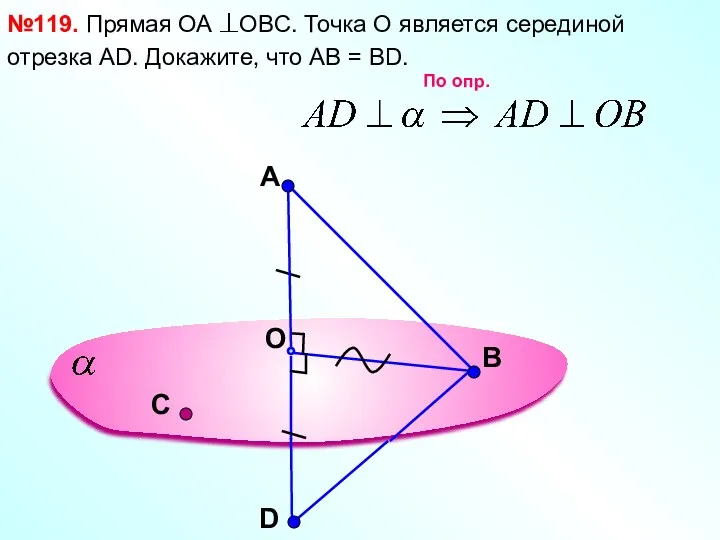
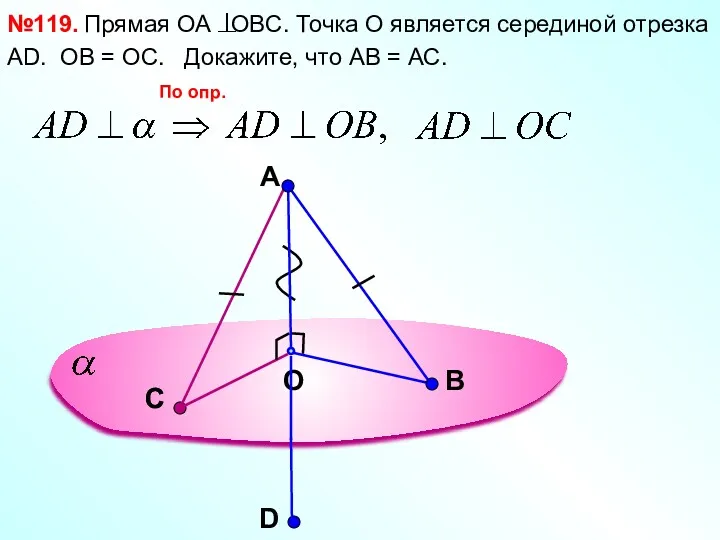
- 9. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD. Докажите, что АВ
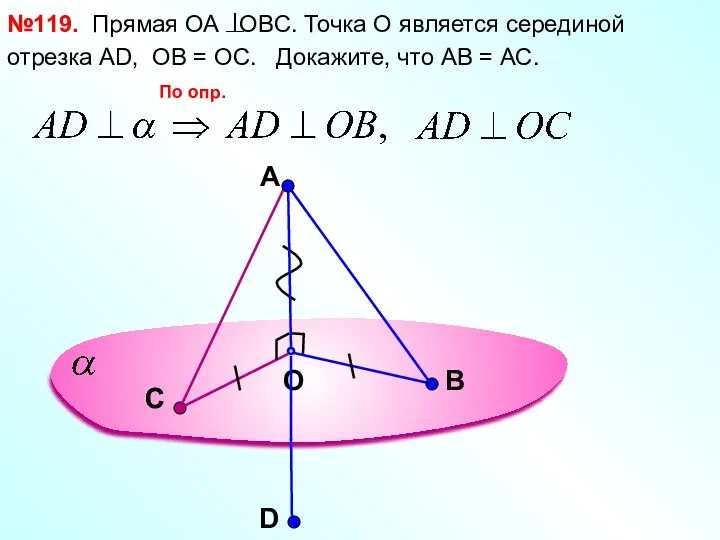
- 10. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD, ОВ = ОС.
- 11. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD. ОВ = ОС.
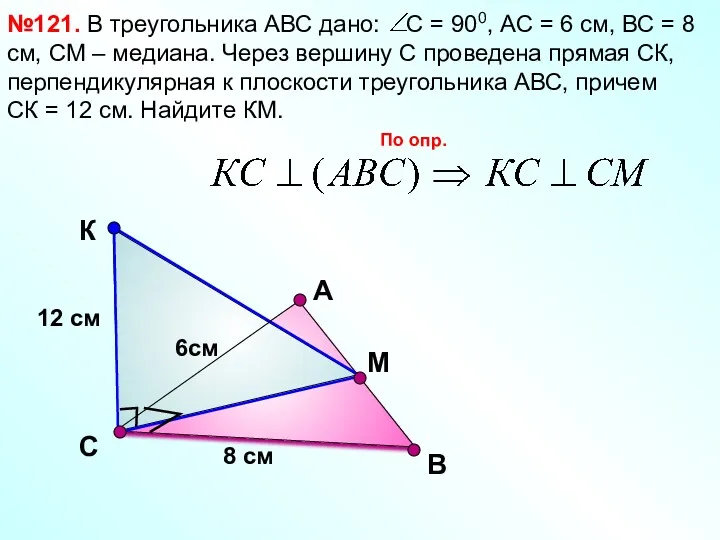
- 12. В №121. В треугольника АВС дано: С = 900, АС = 6 см, ВС = 8
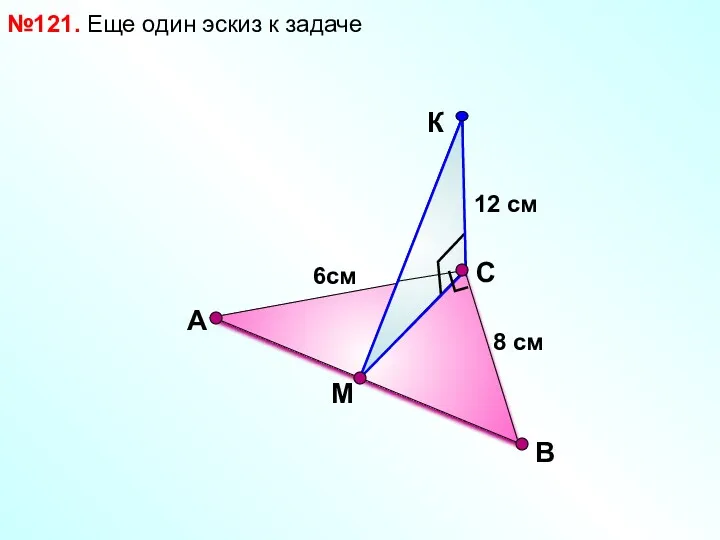
- 13. В №121. Еще один эскиз к задаче С А М 12 см 8 см 6см
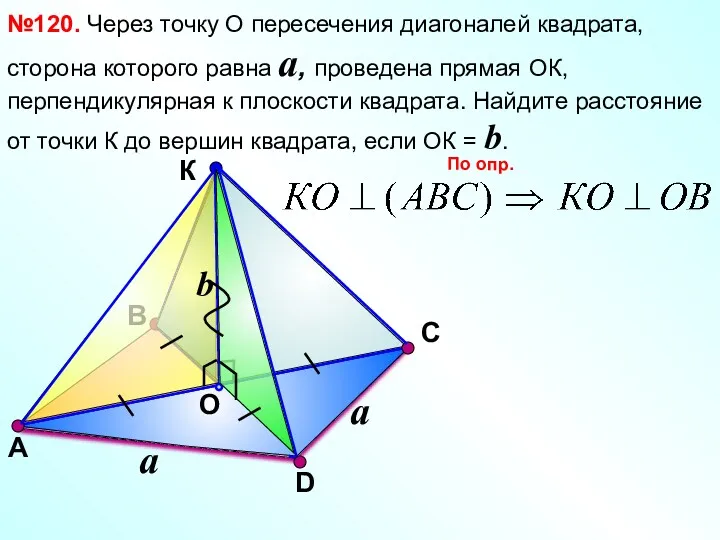
- 14. В К O С №120. Через точку О пересечения диагоналей квадрата, сторона которого равна a, проведена
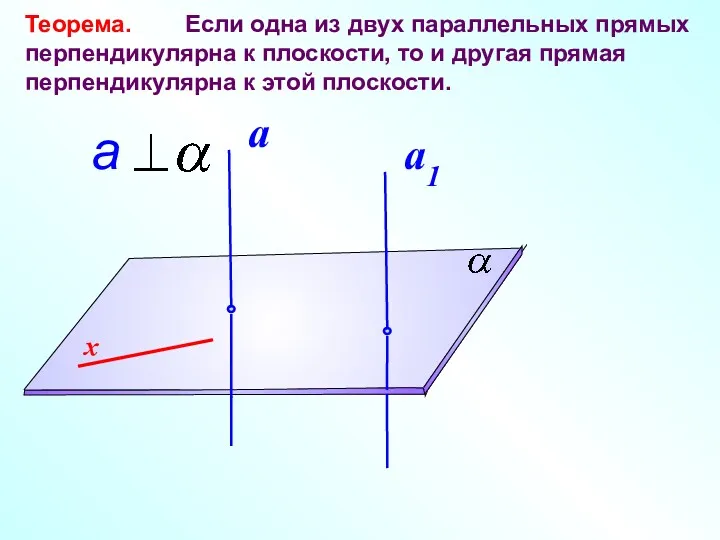
- 15. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к
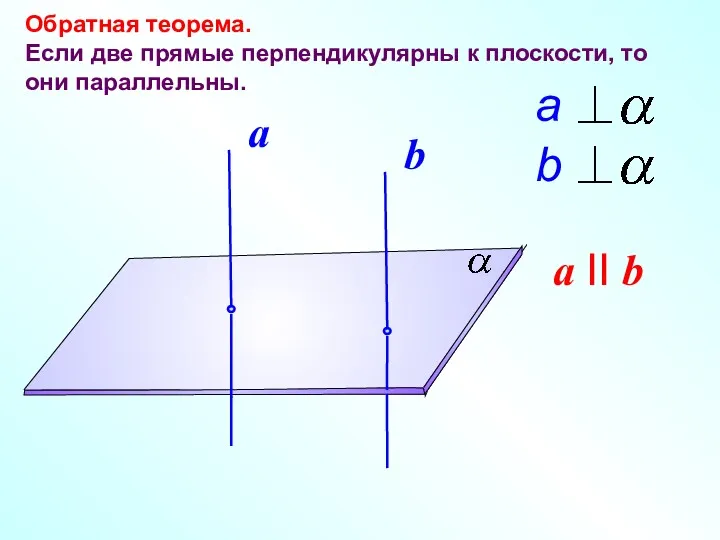
- 16. Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны. a II b
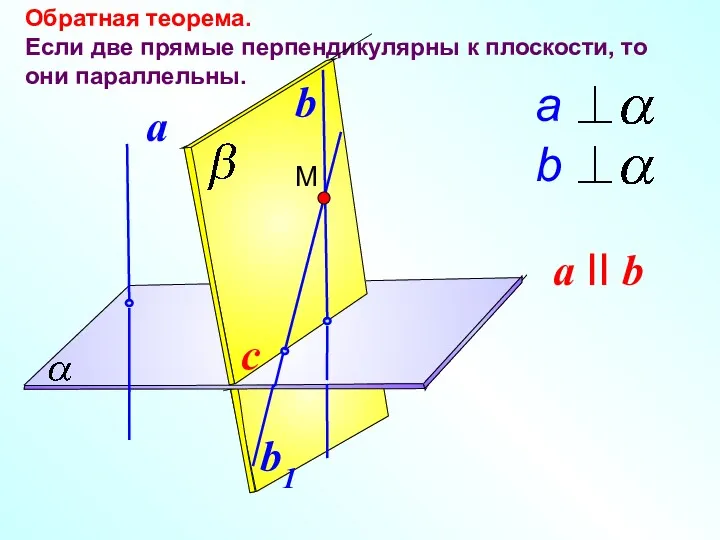
- 17. Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны. a II b c
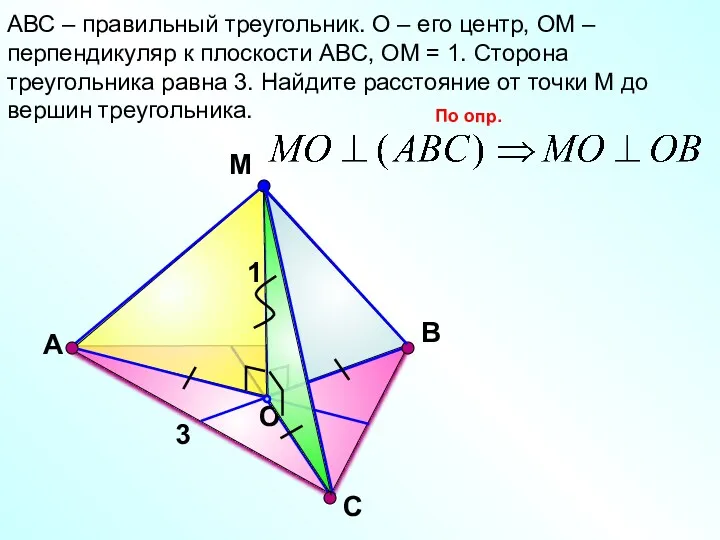
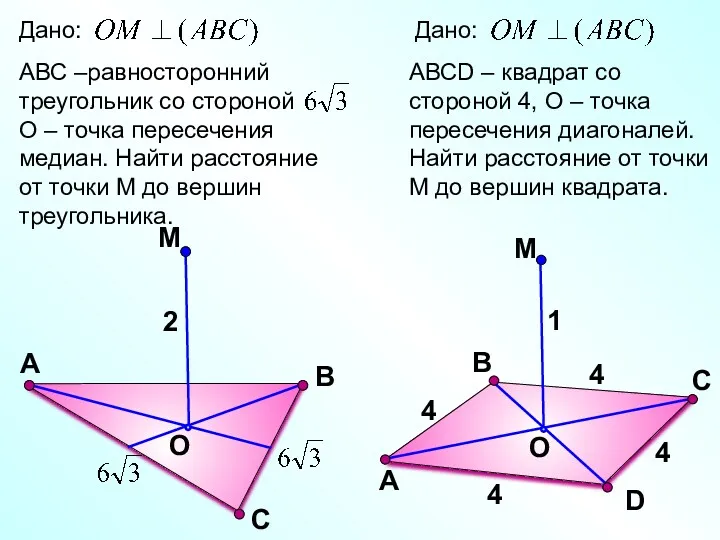
- 18. С М O В АВС – правильный треугольник. О – его центр, ОМ – перпендикуляр к
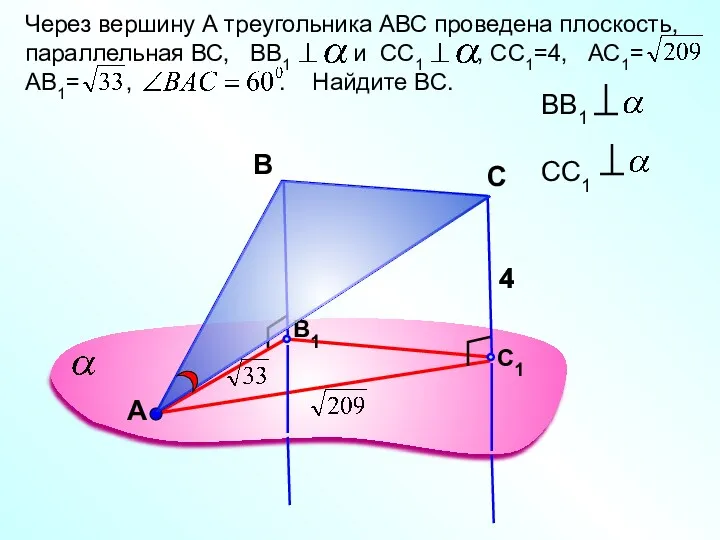
- 19. А Через вершину А треугольника АВС проведена плоскость, параллельная ВС, ВВ1 и СС1 , СС1=4, АС1=
- 20. С М O В А 2 D В М O С А АВСD – квадрат со
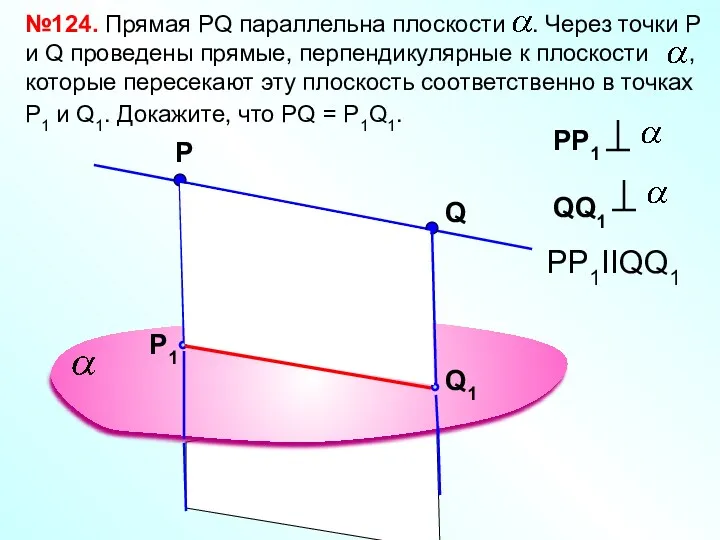
- 21. Р №124. Прямая РQ параллельна плоскости . Через точки Р и Q проведены прямые, перпендикулярные к
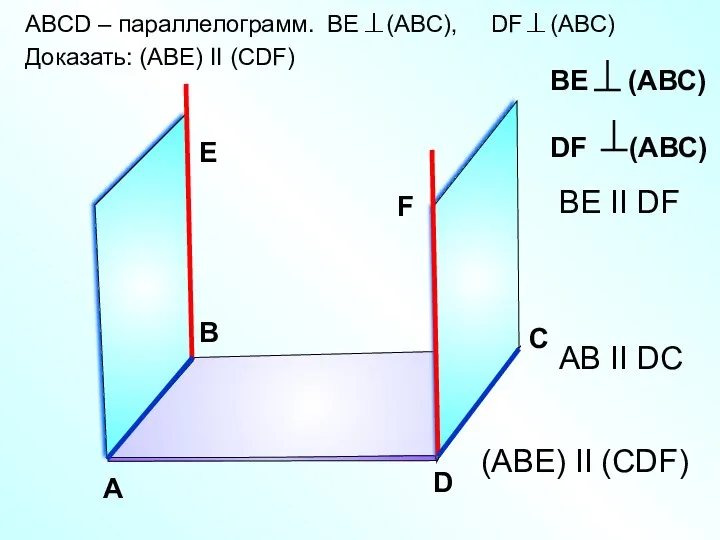
- 22. ABCD – параллелограмм. BE (ABC), DF (ABC) Доказать: (АВЕ) II (СDF) А В С D ВЕ
- 24. Скачать презентацию

 Презентация. Пути формирования (развития) универсальных учебных действий учащихся 1 класса в урочной деятельности по предмету Математика
Презентация. Пути формирования (развития) универсальных учебных действий учащихся 1 класса в урочной деятельности по предмету Математика ЕГЭ профильная математика. Задание № 4
ЕГЭ профильная математика. Задание № 4 Проценты. Сбор багажа
Проценты. Сбор багажа Работа с матрицами и решение систем линейных алгебраических уравнений
Работа с матрицами и решение систем линейных алгебраических уравнений Презентация к уроку математики 4 класс. УМК Школа России
Презентация к уроку математики 4 класс. УМК Школа России Ребусы. Кроссворд Геометрические тела и фигуры
Ребусы. Кроссворд Геометрические тела и фигуры Коэффициент корреляции φ
Коэффициент корреляции φ Тренажёр по математике 1 класс
Тренажёр по математике 1 класс Градустық шамасы берілген бұрышты салу
Градустық шамасы берілген бұрышты салу Проценты и среднее арифметическое в жизни человека
Проценты и среднее арифметическое в жизни человека Методы преобразования плоскостей проекций (Лекция 5)
Методы преобразования плоскостей проекций (Лекция 5) Табличное сложение. Общий приём сложения однозначных чисел с переходом через десяток
Табличное сложение. Общий приём сложения однозначных чисел с переходом через десяток Размещения. Повторение и закрепление пройденного материала
Размещения. Повторение и закрепление пройденного материала Параллельные прямые. Урок геометрии в 7 классе
Параллельные прямые. Урок геометрии в 7 классе Формулы длины окружности и площади круга
Формулы длины окружности и площади круга Здоровьесберегающие технологии на уроках математики
Здоровьесберегающие технологии на уроках математики Презентация по математике для 1 класса УМК Школа России. По теме: Слагаемые. Сумма.
Презентация по математике для 1 класса УМК Школа России. По теме: Слагаемые. Сумма. Весела математика
Весела математика Курс лекций по математике
Курс лекций по математике Современные методы исследования динамических режимов работы асинхронных двигателей. Магистерская диссертация
Современные методы исследования динамических режимов работы асинхронных двигателей. Магистерская диссертация Линейная функция и ее график
Линейная функция и ее график Относительная частота случайного события
Относительная частота случайного события Законы логики
Законы логики Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия
Программа внеурочной деятельности учащихся начальной школы Загадочная геометрия Преемственность начального общего и естественно-математического образования. Семинар
Преемственность начального общего и естественно-математического образования. Семинар Теория вероятностей в заданиях ЕГЭ
Теория вероятностей в заданиях ЕГЭ Математика. 1 класс. Урок 56. Числа 0-10 - Презентация
Математика. 1 класс. Урок 56. Числа 0-10 - Презентация Формула Пика. Площадь многоугольника с целочисленными вершинами
Формула Пика. Площадь многоугольника с целочисленными вершинами