Содержание
- 2. Площадь – это величина, характеризующая размер той части плоскости, которая заключена внутри плоской замкнутой фигуры. Обозначается
- 3. Исторические факты: Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий. Еще в 4
- 4. т.е. умножались полусуммы противоположных сторон. Древние египтяне 4000 лет назад пользовались почти теми же приемами, что
- 5. Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов
- 6. Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной и высотой треугольника, иными словами,
- 7. Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова
- 8. Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на
- 9. Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих
- 10. Эта формула носит название «формулы Герона». На самом деле она была установлена еще в 3 в.
- 11. Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника» Понятие о площади. Свойства площади Обычно говорят,
- 12. Для большей точности измерения можно каждый квадрат палетки разбить на сто квадратов (стороны которых в 10
- 13. Но здесь есть одна тонкость. Вначале мы получили отрезок , где , , в котором содержится
- 14. Второй случай, когда пересечение всех отрезков представляет собой отрезок, а не одну точку, на первый взгляд
- 15. Попробуем теперь измерить площадь фигуры F по Жордану (т. е. с помощью палеток). Какую бы мелкую
- 16. Способ измерения площадей с помощью палеток был предложен в XIX веке французским математиком Камилем Жорданом. Другой
- 17. Другими словами, квадрируемы фигуры, которые можно сколь угодно точно приблизить многоугольниками. Например, площадь круга находят как
- 18. Кроме приведённого выше определения площади с помощью палеток имеется ещё одно, аксиоматическое определение. Прежде чем его
- 19. Очевидно, что площадь , определяемая с помощью палеток, действительно удовлетворяет свойствам А и D. Проверить два
- 20. Заметим, что и в геометрии Лобачевского, и в сферической геометрии площадь определяется теми же аксиомами. Однако
- 21. Понятие о многоугольнике Термин «многоугольник» понимается в математике и, в частности, в школьном курсе математики двояко.
- 22. Понятие о площади многоугольника. Дескриптивное определение В вопросе о площади многоугольник понимается как часть плоскости, ограниченная
- 23. В различных учебниках по геометрии для общеобразовательных учреждений определения площади несколько отличаются друг от друга, но
- 24. Это определение по своему характеру сродни, например, определению арифметического корня ( ): b – есть неотрицательное
- 25. Взгляд на площадь как на первичное понятие сложился ещё в древности. До недавнего времени этого взгляда
- 26. Между тем их вычисления должны были на чём-то основываться – если не на прямом определении, то
- 27. Различные формулы площадей многоугольников Площадь прямоугольника со сторонами и вычисляется по формуле Площадь параллелограмма вычисляется по
- 28. Площадь многоугольника вычисляется по формулам
- 29. Площадь трапеции вычисляется по формулам Площадь правильного треугольника вычисляется по формуле Площадь трапеции вычисляется по формулам
- 30. Площадь произвольного четырёхугольника можно выразить через его стороны а, b, c и сумму В частности, площадь
- 31. где R – радиус круга, вписанного в многоугольник, а Р – периметр прямоугольника. Общий метод для
- 32. Площадь треугольника. Формула Герона Теорема. Площадь треугольника равна половине произведения его стороны на проведённую к ней
- 33. Тогда Но здесь возникает следующий вопрос: почему три возможных полупроизведения основания на высоту для всякого треугольника
- 34. Пользуясь приведённой выше теоремой о площади треугольника очень часто бывает удобно сравнивать площади двух треугольников. Приведём
- 35. Из следствия 2 следуют важные частные случаи: 1.Медиана делит треугольник на две рановеликие части. 2.Биссектриса угла
- 36. Значит В частности, имеет место следующее утверждение: Если два треугольника подобны и сторона одного из них
- 37. В нём всегда найдётся высота, основание которой лежит на стороне треугольника, а не на её продолжении.
- 38. Теперь из первого уравнения системы ( находим Вычитая из первого уравнения системы второе, имеем: Теперь из
- 39. Площадь прямоугольника Теорема. Площадь прямоугольника равна произведению его смежных сторон. Рассмотрим одно из доказательств этой теоремы,
- 40. Площадь трапеции Докажем следующую формулу для вычисления площади трапеции: Площадь трапеции равна произведению одной из боковых
- 41. Площадь четырёхугольника Докажем следующую теорему: площадь произвольного выпуклого четырёхугольника может быть определена по формуле: Доказательство. Пусть
- 42. что и требовалось доказать. Теорема имеет ряд следствий. Выполним равносильные преобразования, получим что и требовалось доказать.
- 43. Доказательство. Так как у описанного четырёхугольника суммы противолежащих сторон равны, т. е. Следствие 2. Площадь произвольного
- 44. Формула Пика Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник
- 45. Назовём треугольник достижимым, если в его вершинах могут одновременно оказаться три кузнечика, которые вначале были в
- 46. Фигуры с наибольшей площадью Трапеция или прямоугольник ??? Рассмотрение этого пункта начнём с решения задачи. Задача.
- 47. Решение Прямоугольников с обводом в 40 вёрст может быть очень много, и каждый имеет другую площадь.
- 48. Единицы измерения площадей. Старые русские меры площадей. В «Русской правде»- законодательном памятнике, который относился к 11-13
- 49. Другая единица, равная половине десятины, называлась четверть. Налоговой единицей земли была соха (количество пахотной земли, которое
- 50. Квадратная миля (США) (stature square mile) 2,58999 кв.км. Акр (acre) 4046,86 м2=0,404686 га. Квадратный ярд (square
- 51. Теоремы площадей фигур. Теорема 1. Площадь квадрата равна квадрату его стороны. Докажем что площадь S квадрата
- 52. S = a * h. Пусть ABCD – данный параллелограмм. Если он не является прямоугольником, то
- 53. A Теорема 3. Площадь треугольника равна половине произведения его стороны на проведенную к ней высоту :
- 54. A Площадь параллелограмма равна сумме площадей треугольников ABC и CDA. Так как эти треугольники равны, то
- 55. b Теорема 3.1. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
- 56. A Теорема 4 . Площадь трапеции равна произведению полусуммы его оснований на высоту (рис.4.). Доказательство. Пусть
- 57. A Диагональ AC трапеции разбивает ее на два треугольника: ABC и CDA. Следовательно, площадь трапеции равна
- 58. Задачи по теоремам: Задача по теореме 1 Дано: ABCD – квадрат, a – сторона квадрата равная
- 59. Задача по теореме 2. Дано: ABCD – параллелограмм, h – высота равная 3 см. сторона a
- 60. Задача по теореме 3. Дано: ABC - треугольник, h – высота равная 4 см. a –
- 61. Задача по теореме 4. Дано: ABCD – трапеция, h – высота равная 4 см. а –
- 62. Задача: В ΔABC проведены биссектрисы AK и CE. Найти отношение площадей ΔABC и ΔAEK, если AB=21,
- 63. Ответ: Решение: 1.Т.к.AK-биссектриса ΔABC, то Отсюда 2.Т.к. CE-биссектриса ΔABC, то Отсюда 3.Т.к. ΔABC и ΔBEK имеют
- 64. Задача: В равнобедренной трапеции высота равна H, а диагонали взаимно перпендикулярны. Найти площадь трапеции. 1 способ.
- 65. 2 способ
- 66. Ответ: 1 способ: ΔAOF и ΔBOK – прямоугольные и равнобедренные, тогда OK=BK, OF=AF, OK+OF=BK+AF= BC+ AD=
- 67. Задача: Площадь треугольника Все высоты треугольника меньше 1. Может ли его площадь быть больше 10000 квадратных
- 68. Ответ: Может. Таким будет, например, равнобедренный треугольник, основание которого равно 80000, а высота к основанию равна
- 69. Задача: Странный треугольник Стоpоны тpеyгольника pавны 13, 18 и 31 см. Чемy pавна площадь?
- 70. Ответ: 0, т.к. получится не треугольник, а линия. В любом треугольнике всегда сумма длин двух любых
- 71. Заключение. Площади фигур имеют огромное значение в геометрии, как в науке. Ведь площадь это одна из
- 73. Скачать презентацию
 Эконометрика. Показатели экономических процессов как случайные величины. Аспекты эконометрического моделирования. (Тема 2)
Эконометрика. Показатели экономических процессов как случайные величины. Аспекты эконометрического моделирования. (Тема 2) Роль учителя и современных педагогических технологий в формировании положительной мотивации к изучению математики
Роль учителя и современных педагогических технологий в формировании положительной мотивации к изучению математики Повторение пройденного. Заполните таблицу
Повторение пройденного. Заполните таблицу Сложение и вычитание положительных и отрицательных чисел. (6 класс)
Сложение и вычитание положительных и отрицательных чисел. (6 класс) Цифровой образовательный ресурс по познавательному направлению развития ребенка
Цифровой образовательный ресурс по познавательному направлению развития ребенка Задачи на построение
Задачи на построение Урок математики по теме Ломаная линия
Урок математики по теме Ломаная линия Комбинаторика. Основные формулы
Комбинаторика. Основные формулы Презентация Счёт в пределах 1000
Презентация Счёт в пределах 1000 Среднее арифметическое. 5 класс
Среднее арифметическое. 5 класс Параллельный перенос
Параллельный перенос Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Презентация к уроку математики Арифметический диктант
Презентация к уроку математики Арифметический диктант Определение логарифма
Определение логарифма Базовые компоненты эконометрики
Базовые компоненты эконометрики Презентация открытого урока по математике Поиск чемпионов
Презентация открытого урока по математике Поиск чемпионов Иррациональные уравнения. Методы решения
Иррациональные уравнения. Методы решения Метрология. Измерение
Метрология. Измерение Історія розвитку комбінаторики та деякі її застосування
Історія розвитку комбінаторики та деякі її застосування Проценты. Обобщающий урок
Проценты. Обобщающий урок Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями Презентация по математики 1 класс Повторение сложения и вычитания с числом 2
Презентация по математики 1 класс Повторение сложения и вычитания с числом 2 Заниматика. 1 класс
Заниматика. 1 класс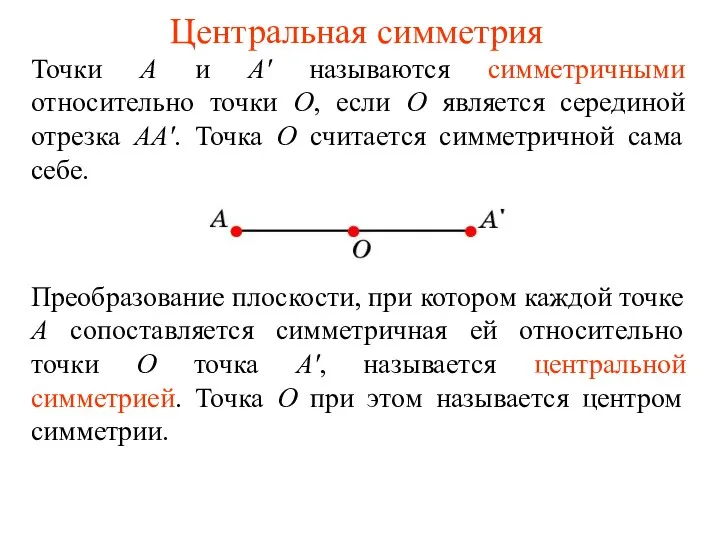 Центральная симметрия
Центральная симметрия ЕГЭ. Текстовые задачи. Теория вероятностей. (Лекция 1)
ЕГЭ. Текстовые задачи. Теория вероятностей. (Лекция 1) 20231126_geometriya_9_klass_p.6
20231126_geometriya_9_klass_p.6 Возведение в степень произведения и степени
Возведение в степень произведения и степени Трапеция
Трапеция