Содержание
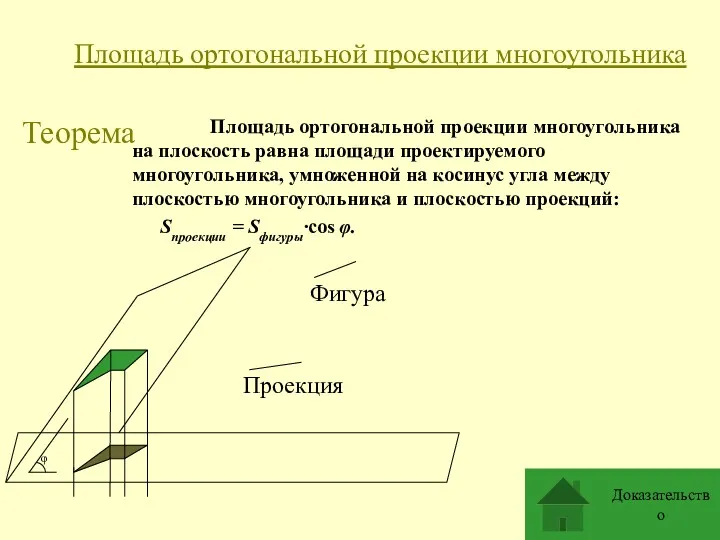
- 2. Теорема Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между
- 3. Доказательство. Пусть AC || l = α∩π. Тогда высота BH┴l, SΔABC = 0,5AC·BH. AC || l
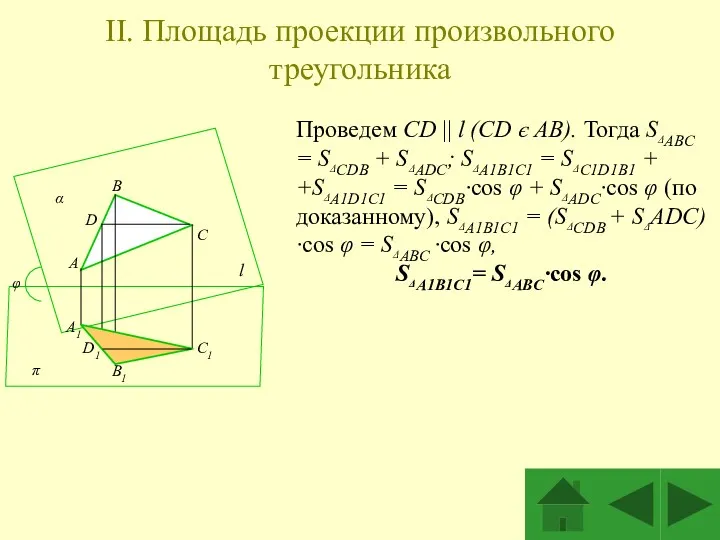
- 4. II. Площадь проекции произвольного треугольника Проведем CD || l (CD є AB). Тогда SΔABC = SΔCDB
- 5. Дано: A(BC)M = 60º; AM ┴(BCM). Найти: SABC:SMBC. Решение. AM ┴(BCM), значит, M – ортогональная проекция
- 6. Задача 4.090. Квадрат ABCD перегнули по его диагонали BC так, что образовался острый двугранный угол α.
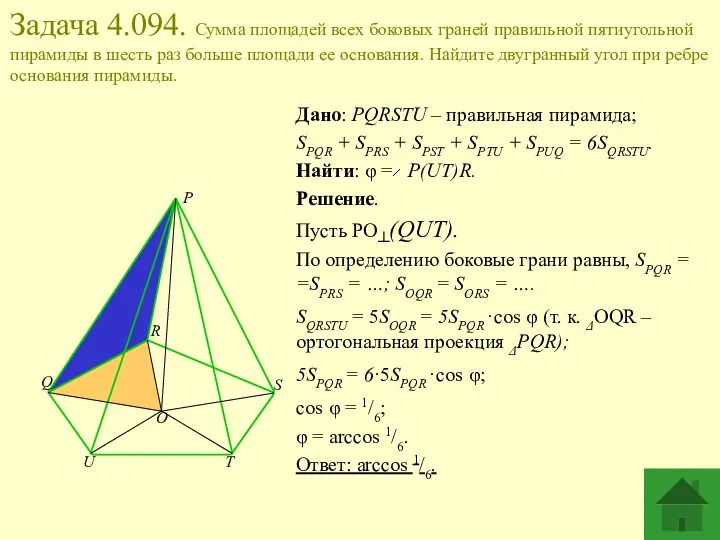
- 7. Задача 4.094. Сумма площадей всех боковых граней правильной пятиугольной пирамиды в шесть раз больше площади ее
- 8. Задача 4.095. В правильной треугольной пирамиде MABC все боковые ребра образуют с плоскостью основания углы, равные
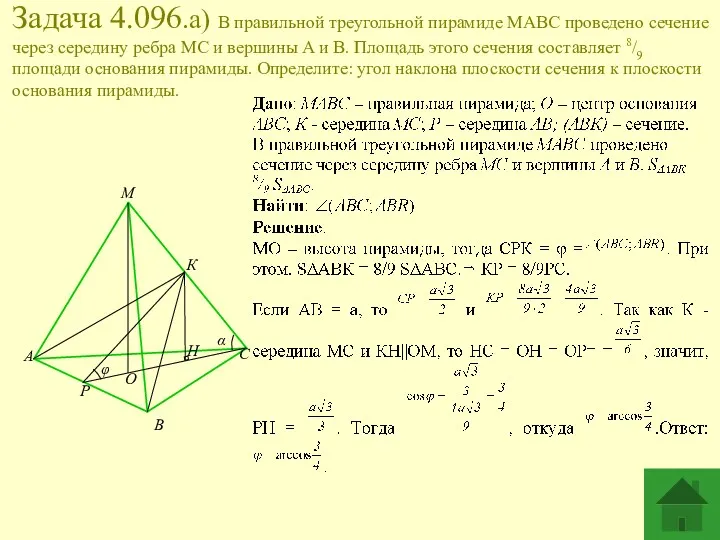
- 9. Задача 4.096.а) В правильной треугольной пирамиде MABC проведено сечение через середину ребра MC и вершины A
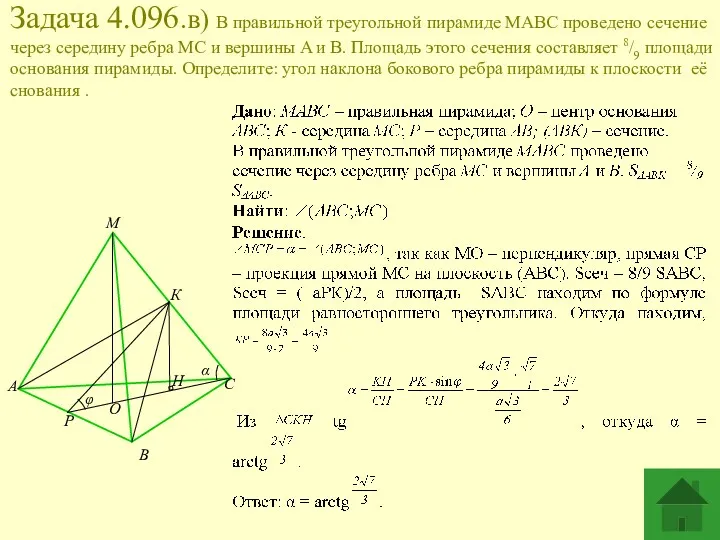
- 10. Задача 4.096.в) В правильной треугольной пирамиде MABC проведено сечение через середину ребра MC и вершины A
- 11. Задача 4.097. В правильной четырехугольной пирамиде МАВСD через ребро АВ и середину ребра МС проведено сечение,
- 12. Задача 4.097.В правильной четырехугольной пирамиде МАВСD через ребро АВ и середину ребра МС проведено сечение, площадь
- 13. A B M C P H φ Задача 4.098. К плоскости треугольника АВС по одну от
- 14. Дано: ABCD – квадрат; AM┴(ABC); AM = 10; (ABC; MBC) = 45º. Найти: SMBC. Решение. (ABC;
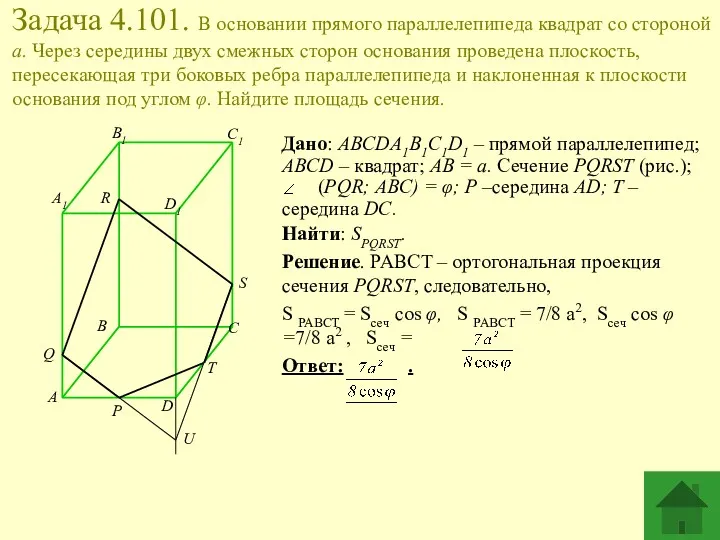
- 15. Задача 4.101. В основании прямого параллелепипеда квадрат со стороной a. Через середины двух смежных сторон основания
- 16. A B C H L M O A1 B1 C1 K1 O1 K φ φ Задача
- 17. A B C H L M O A1 B1 C1 K1 O1 K φ φ Задача
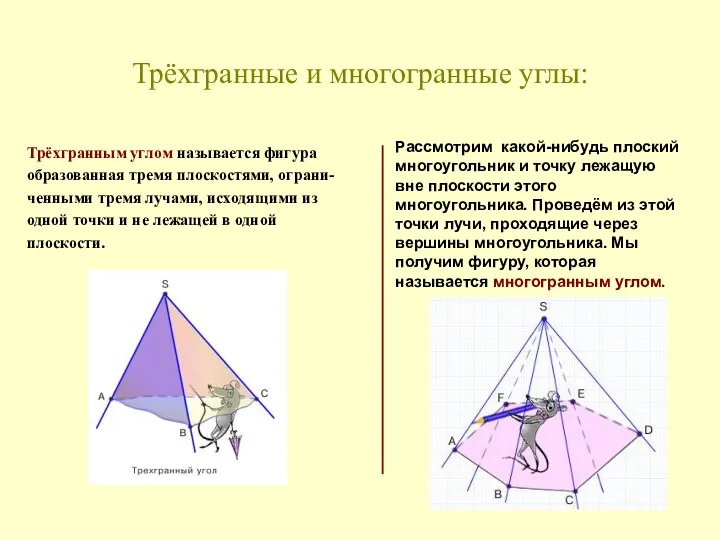
- 18. Трёхгранные и многогранные углы: Трёхгранным углом называется фигура образованная тремя плоскостями, ограни- ченными тремя лучами, исходящими
- 19. Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими
- 20. Определение. Трехгранные углы называются равными если равны все их соответствующие плоские и двугранные углы. Признаки равенства
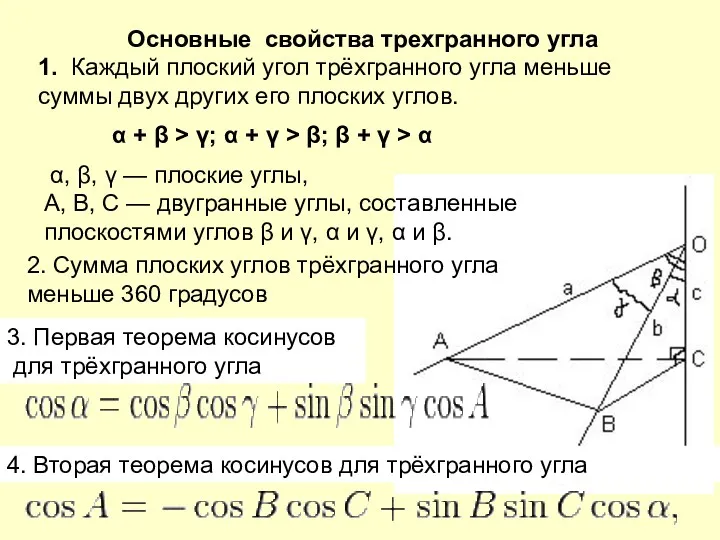
- 21. Основные свойства трехгранного угла 1. Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских
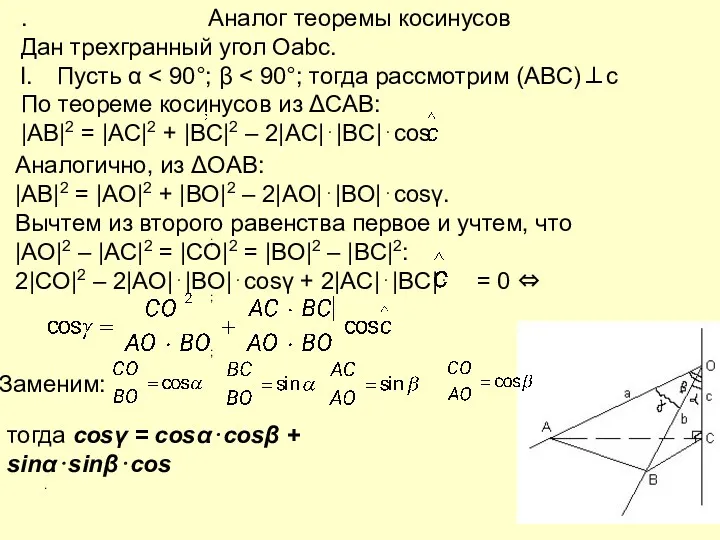
- 22. . . Дан трехгранный угол Оabc. Пусть α По теореме косинусов из ΔCАВ: |AB|2 = |AC|2
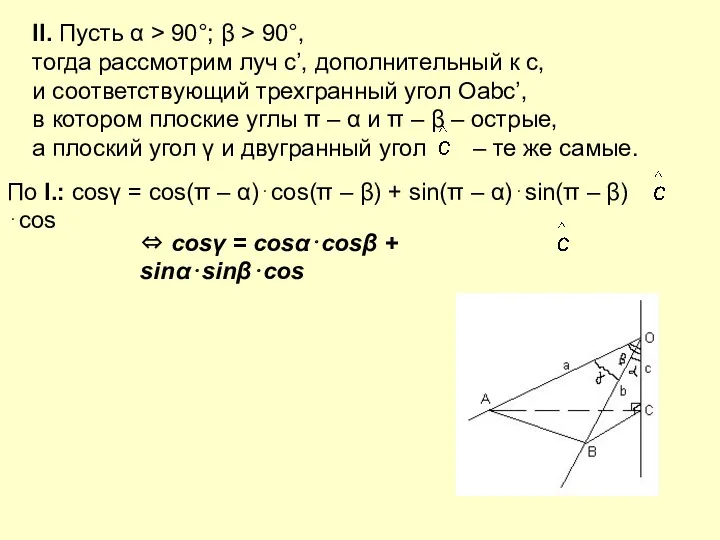
- 23. II. Пусть α > 90°; β > 90°, тогда рассмотрим луч с’, дополнительный к с, и
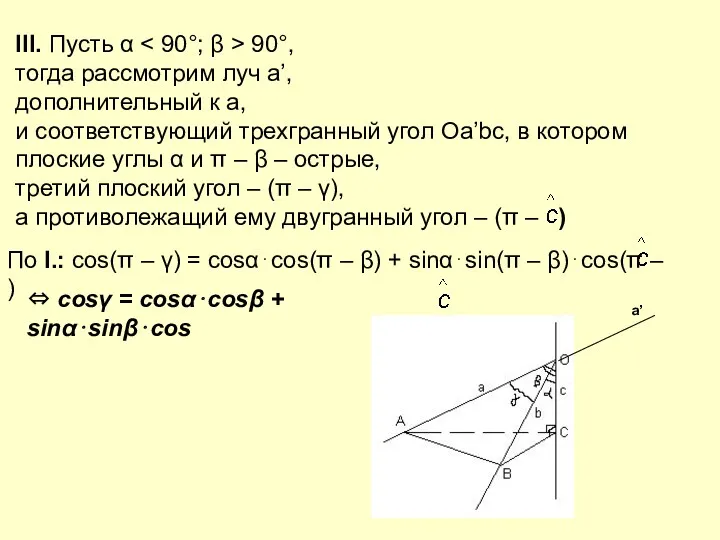
- 24. III. Пусть α 90°, тогда рассмотрим луч a’, дополнительный к a, и соответствующий трехгранный угол Оа’bс,
- 25. IV. Пусть α = 90°; β = 90°, тогда γ = и равенство, очевидно, выполняется. Если
- 26. , 5. Теорема синусов Многогранный угол, внутренняя область которого расположена по одну сторону от плоскости каждой
- 27. Многогранники. Правильные многогранники.
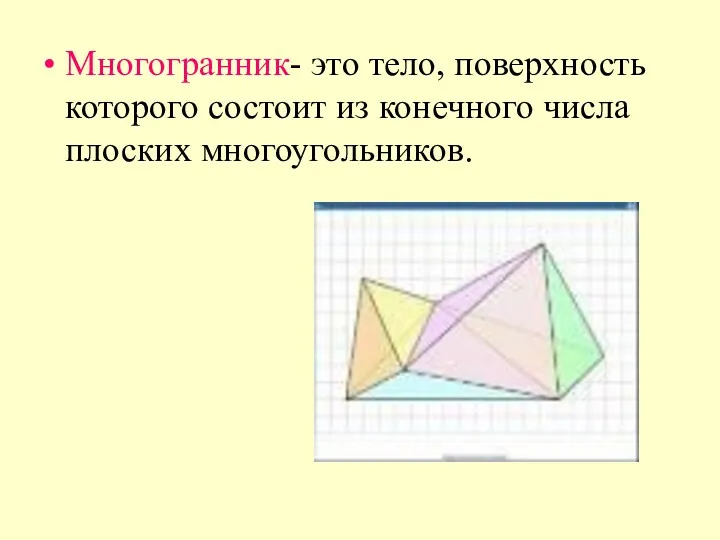
- 28. Многогранник- это тело, поверхность которого состоит из конечного числа плоских многоугольников.
- 29. Грани многогранника - это многоугольники, которые его образуют. Ребра многогранника - это стороны многоугольников. Вершины многогранника
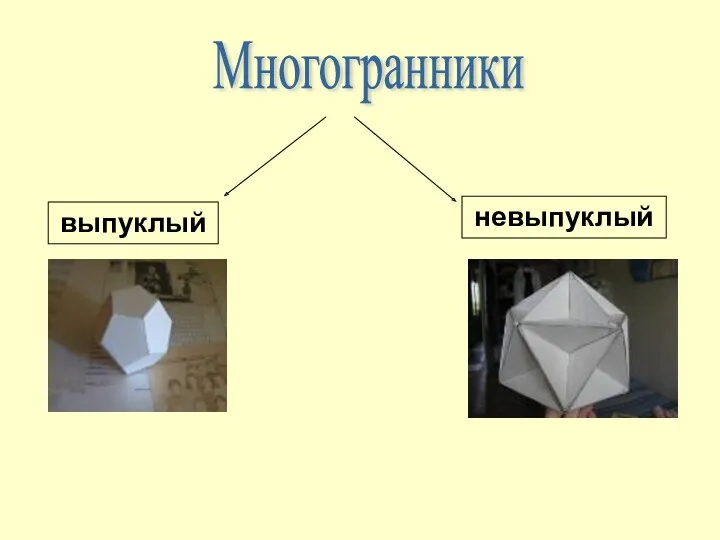
- 30. выпуклый невыпуклый Многогранники
- 31. Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности.
- 32. Правильные многогранники Если грани многогранника являются правильными многоугольниками с одним и тем же числом сторон и
- 33. пришли из Древней Греции, в них указывается число граней: «эдра» − грань; «тетра» − 4; «гекса»
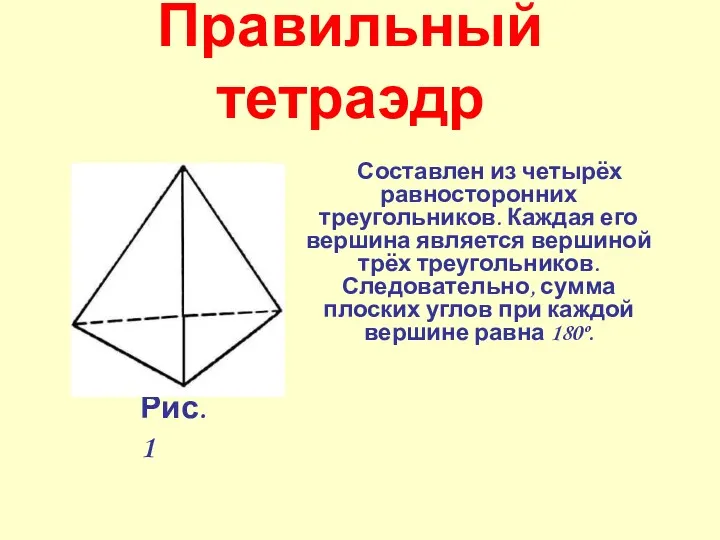
- 34. Правильный тетраэдр Составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма
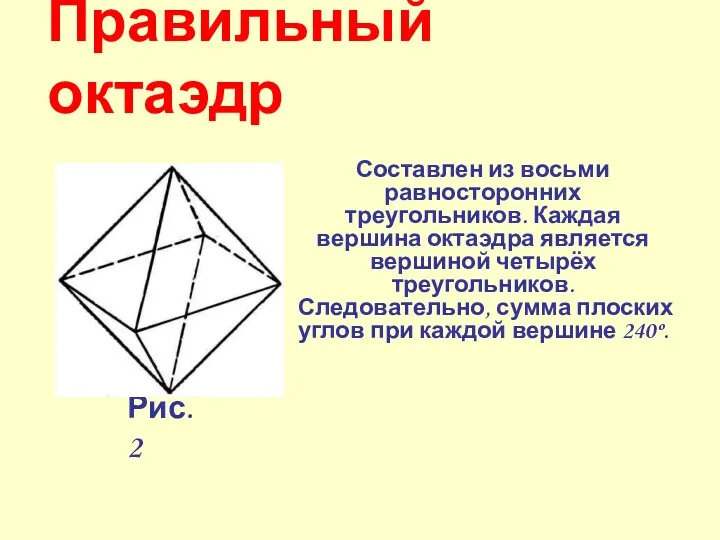
- 35. Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. Следовательно, сумма плоских углов
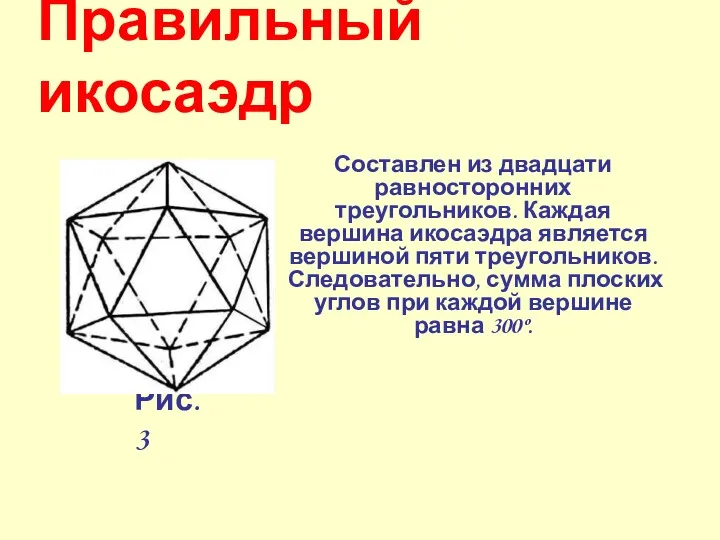
- 36. Правильный икосаэдр Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма
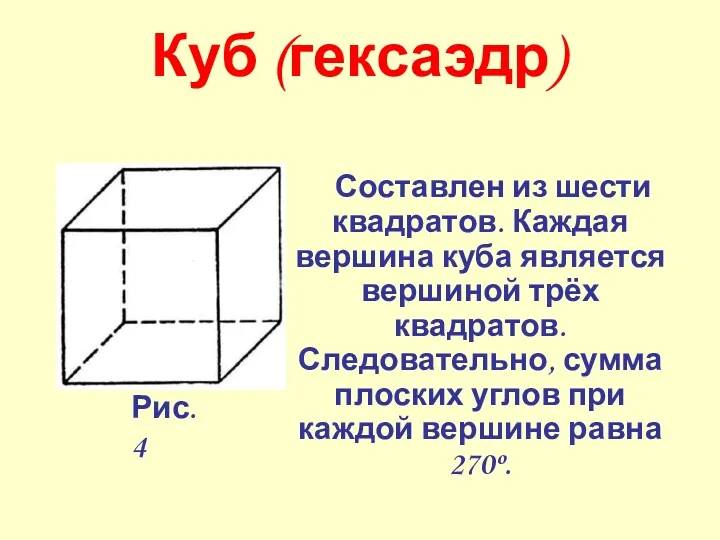
- 37. Составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. Следовательно, сумма плоских углов при
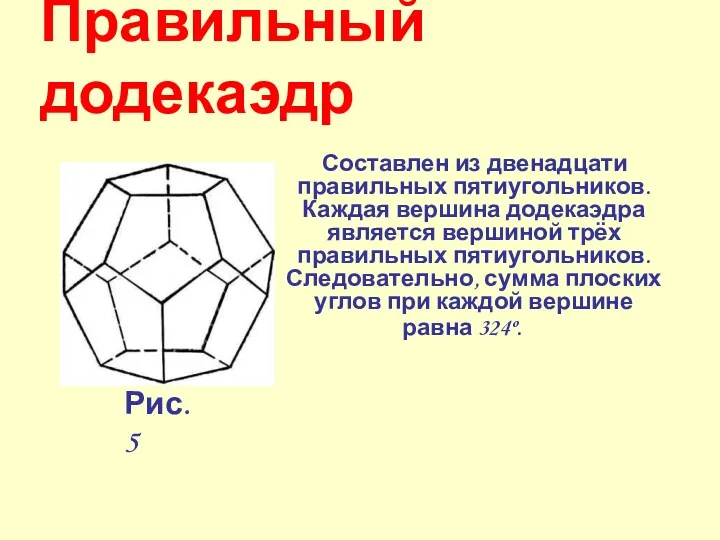
- 38. Правильный додекаэдр Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно,
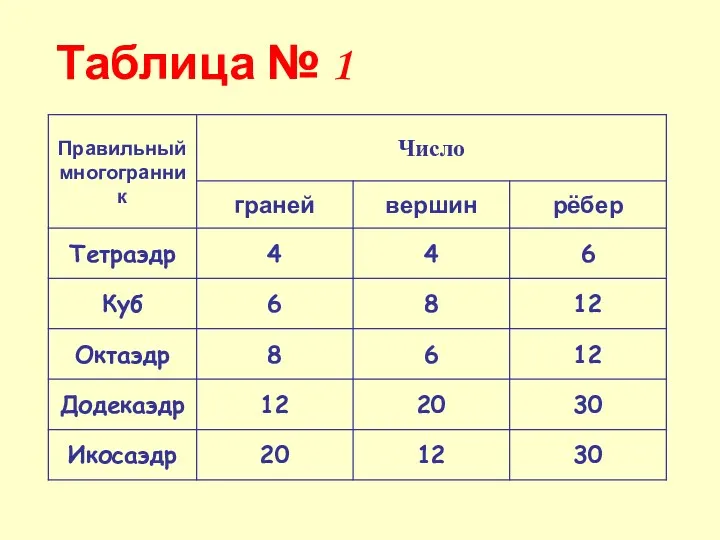
- 39. Таблица № 1
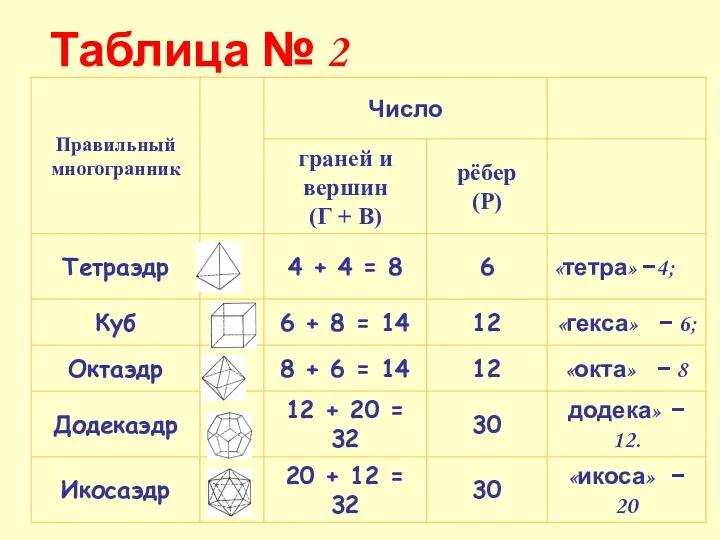
- 40. Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В
- 41. Таблица № 2
- 43. Скачать презентацию




















 Формула бинома Ньютона. Свойства биномиальных коэффициентов
Формула бинома Ньютона. Свойства биномиальных коэффициентов Устный счет. Сложение с переходом через десяток. Часть 2
Устный счет. Сложение с переходом через десяток. Часть 2 Математика в календаре
Математика в календаре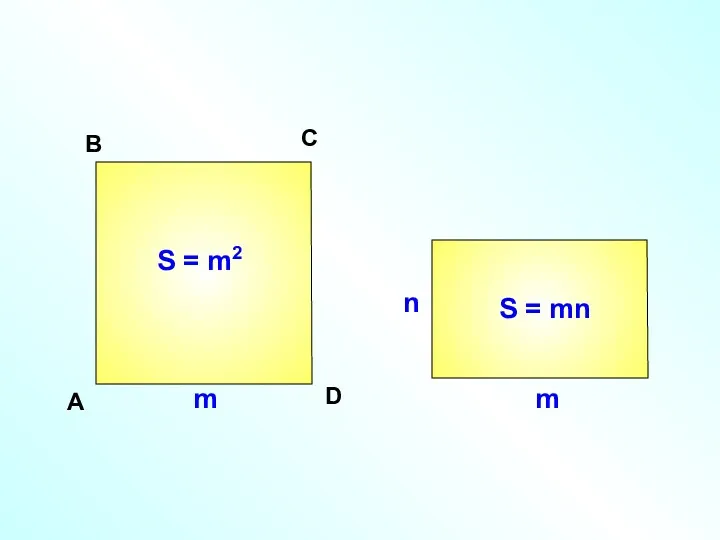 Площади фигур
Площади фигур Предел функции
Предел функции Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов
Точность и качество измерений: понятия погрешности, точности, достоверности, сходимости, правильности. Классы точности приборов Умножение круглых чисел
Умножение круглых чисел Цилиндр. Понятие цилиндрической поверхности
Цилиндр. Понятие цилиндрической поверхности Числовые промежутки
Числовые промежутки Анализ эмпирических данных. (Тема 9)
Анализ эмпирических данных. (Тема 9) Функция y=sinx и её график
Функция y=sinx и её график Проблема качества систем автоматического управления. Тема 4
Проблема качества систем автоматического управления. Тема 4 Презентация Больше, меньше 1 класс
Презентация Больше, меньше 1 класс Самостоятельная математическая деятельность детей дошкольного возраста
Самостоятельная математическая деятельность детей дошкольного возраста Первый признак равенства треугольников. (7 класс)
Первый признак равенства треугольников. (7 класс)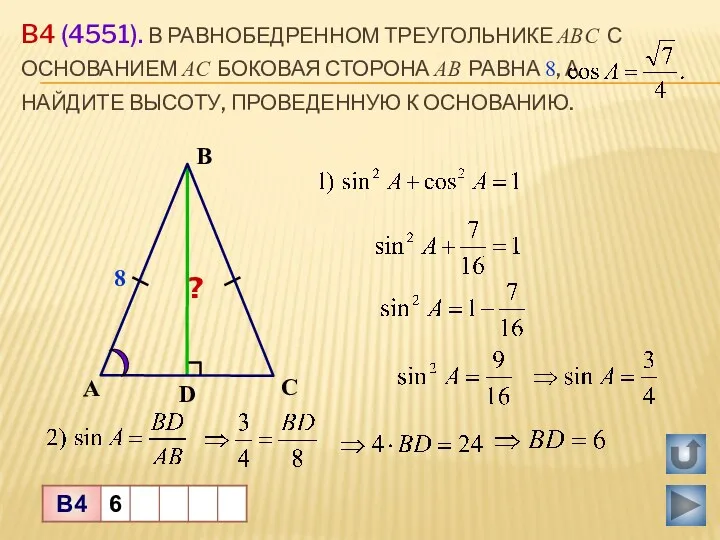 Знаки тригонометрических функций
Знаки тригонометрических функций Урок математики в 1 классе ( Гармония).
Урок математики в 1 классе ( Гармония). Компоненты суммы
Компоненты суммы Письменное деление многозначных чисел на трехзначное число
Письменное деление многозначных чисел на трехзначное число Урок математики в 4 классе по теме: Прямоугольный параллелепипед. Куб.
Урок математики в 4 классе по теме: Прямоугольный параллелепипед. Куб. Интегральное исчисление функций одной переменной
Интегральное исчисление функций одной переменной Конспект занятия Путешествие по стране логики
Конспект занятия Путешествие по стране логики Перпендикуляр и наклонные Перпендикуляр из точки А к плоскости a
Перпендикуляр и наклонные Перпендикуляр из точки А к плоскости a Математическая игра Звёздный час
Математическая игра Звёздный час Множення десяткових дробів
Множення десяткових дробів Усечённая пирамида
Усечённая пирамида Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс
Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа