Слайд 2

1. Опрацювати наступні питання лекційного матеріалу:
- частинні похідні функцій багатьох змінних;
-
повний диференціал функції;
- частинні похідні другого і вищих порядків;
- повний диференціал другого порядку функцій двох змінних.
2. Самостійно опрацювати питання:
2.1. Похідна за напрямком. Градієнт.
2.2. Застосування диференціала до наближених обчислень.
Слайд 3

2.1. Похідна за напрямком. Градієнт.
Означення. Нехай функція визначена в деякому
околі точки ;
деякий промінь з початком в точці ; - точка на цьому промені, яка належить околу, що розглядається довжина відрізка .
Границя , якщо вона існує, називається похідною функції
за напрямом у точці і позначається .
Теорема 4. Якщо функція має в точці неперервні частинні похідні, тоді в цій точці існує похідна за будь-яким напрямом ,
причому (2.1.1)
Де і - значення частинних похідних функції у точці
Похідна за напрямом характеризує швидкість змінювання функції
в точці за напрямом .
Слайд 4

Наприклад. Знайти похідну функції у точці (1; 1) за напрямом
.
Знайдемо та обчислимо частинні похідні в точці (1;1) функції :
Тоді за формулою похідної за напрямом дістанемо:
.
Означення. Вектор з координатами , який характеризує напрям
максимального зростання функції
у точці , називається градієнтом функції у цій точці і позначається
. (2.1.2)
Наприклад. Знайти градієнт функції
у точці (1; 2; -1).
Знайдемо та обчислимо частинні похідні в точці (1; 2; -1):
Слайд 5
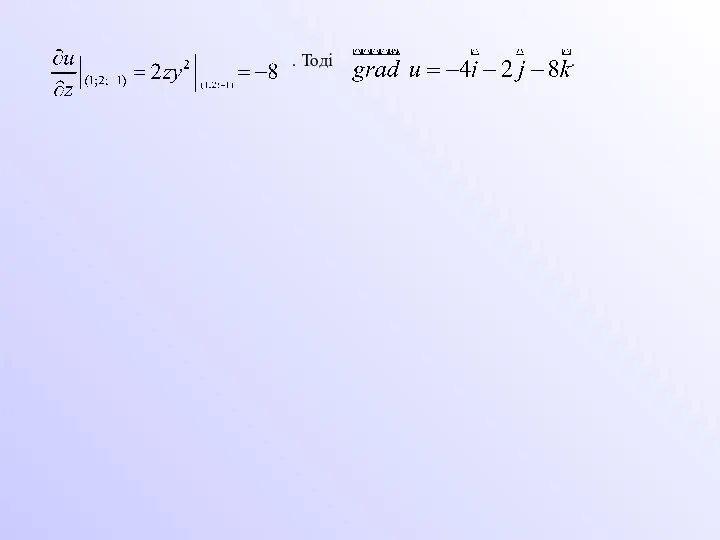
Слайд 6

2.2. Застосування диференціала до наближених обчислень.
Якщо функція диференційована в точці то
виконується рівність або
Узявши в наближеній рівності , дістанемо:
(2.2.1)
На формулі (2.2.1) ґрунтується алгоритм використання диференціала для наближених обчислень.
Наприклад. Обчислити наближено , замінюючи приріст функції її повним диференціалом. Відомо, що . Треба обчислити . Розглянемо функцію .
Введемо позначення:
. Скористуємось наближеною формулою:
, тобто
(2.2.2)
Знайдемо
,
Слайд 7

Підставляючи в (2.2.2), одержимо: = =
Завдання для самостійної роботи:
1.Знайти градієнт функції
та величину градієнта функції :
в точці
а) ; д) ;
б) ; е) ;
в) ; є) ;
г) ; ж) .



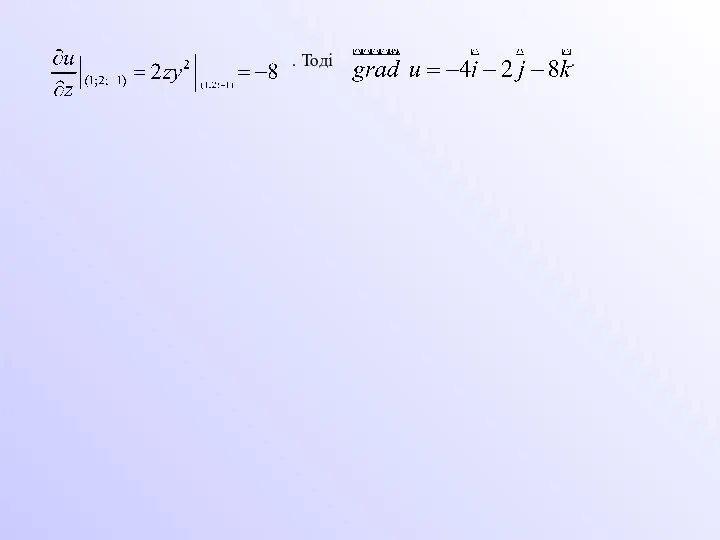


 Случаи вычитания 17 -, 18 -
Случаи вычитания 17 -, 18 - Descriptive statistics
Descriptive statistics Правильные и неправильные дроби. Понятия
Правильные и неправильные дроби. Понятия Основное свойство дроби
Основное свойство дроби Презентация: Деление многозначного числа с нулём на конце делимого(и остатком).
Презентация: Деление многозначного числа с нулём на конце делимого(и остатком). Презентация Как люди научились считать Диск
Презентация Как люди научились считать Диск Теоремы об углах, образованных двумя параллельными прямыми и секущей
Теоремы об углах, образованных двумя параллельными прямыми и секущей Формула площади прямоугольника и квадрата
Формула площади прямоугольника и квадрата Отношением отрезков AB и CD называется отношение их длин
Отношением отрезков AB и CD называется отношение их длин Решение неравенств методом интервалов
Решение неравенств методом интервалов Основы финансовой математики
Основы финансовой математики Решение геометрических задач ГИА №26
Решение геометрических задач ГИА №26 Углы и многоугольники (5 класс)
Углы и многоугольники (5 класс) Межпредметные связи в математике. Подготовка к ЕГЭ
Межпредметные связи в математике. Подготовка к ЕГЭ Правильные и неправильные дроби
Правильные и неправильные дроби Два замечательных предела
Два замечательных предела Додавання та віднімання дробів з різними знаменниками
Додавання та віднімання дробів з різними знаменниками Презентация Геометрические фигуры
Презентация Геометрические фигуры Задания от Буратино (Математика, 1 класс)
Задания от Буратино (Математика, 1 класс) Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ
Урок математики в 4 классе Решение задач. Когда количество одинаковое ПНШ Слагаемые и сумма
Слагаемые и сумма Презентация к уроку математики. 1 класс. Сантиметр. УМК Школа России
Презентация к уроку математики. 1 класс. Сантиметр. УМК Школа России Случайные погрешности и законы распределения
Случайные погрешности и законы распределения Загадки пирамид
Загадки пирамид Переместительное свойство умножения
Переместительное свойство умножения Вектор - любой направленный отрезок
Вектор - любой направленный отрезок Извлечение квадратных корней из больших чисел без калькулятора
Извлечение квадратных корней из больших чисел без калькулятора Аксиомы стереометрии. Параллельность в пространстве
Аксиомы стереометрии. Параллельность в пространстве