Содержание
- 2. ПЛАН 1.МНОЖЕСТВО 2. ВИДЫ МНОЖЕСТВ 4. ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ 3. ОПЕРАЦИИ НА МНОЖЕСТВАХ
- 3. УМЕНИЯ 1. НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ 2. НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ 3. ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА 4.
- 4. Основу теории математики составляют понятия и отношения между этими понятиями, которые устанавливаются при помощи соответствующих аксиом
- 5. основатель теории множеств Георг Кантор (1845-1918) Понятие множества является одним из наиболее общих и наиболее важных
- 6. Одним из фундаментальных, неопределяемых математических понятий является понятие множества Множество можно представить себе как соединение, совокупность,
- 7. Величиной называется все что может быть измерено и выражено числом Множеством называется совокупность некоторых элементов. Элементами
- 8. Придумай название для предметов и животных, собранных вместе:
- 9. Придумай название для предметов и животных, собранных вместе: КОЛЛЕКЦИЯ МАРОК НАБОР КАРАНДАШЕЙ СТАЯ ПТИЦ ЧАЙНЫЙ СЕРВИЗ
- 10. Определение Предметы, из которых состоит множество, называются его элементами например, буква К – элемент множества букв
- 11. Обозначают множества заглавными буквами латинского алфавита или символически с помощью фигурных скобок, в которых указываются его
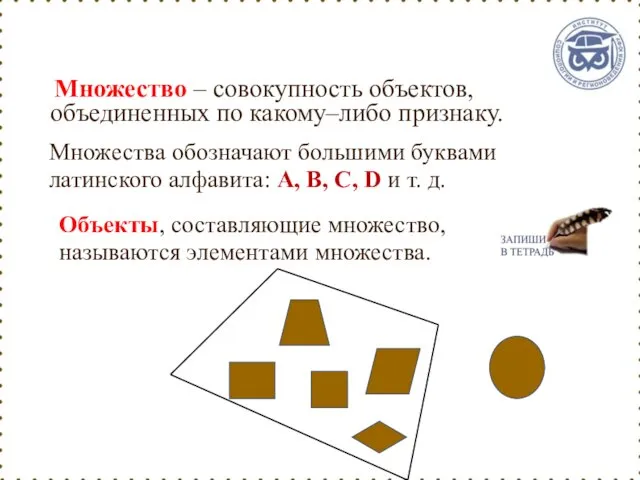
- 12. Множество – совокупность объектов, объединенных по какому–либо признаку. Объекты, составляющие множество, называются элементами множества. Множества обозначают
- 13. Принадлежность предмета некоторому множеству обозначают с помощью символа ∈ (в противном случае используется символ ∉). Запись
- 14. Основными способами задания множества являются: 1) перечисление всех его элементов: А={а1, а2, …, аn}; 2) описание
- 15. Например, характеристическим свойством натуральных чисел является возможность их использования при счете каких-либо предметов. Говоря о множестве
- 16. Множество четырехугольников Пространственные тела 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… Квадраты
- 17. множество людей на Солнце множество прямых углов равностороннего треугольника множество точек пересечения двух параллельных прямых Определение:
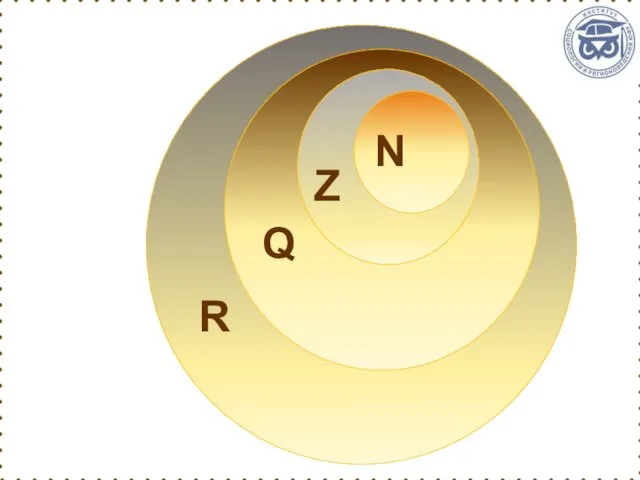
- 18. Обозначения некоторых числовых множеств: N – множество натуральных чисел; Z – множество целых чисел; Q –
- 19. N={1,2,3,4,…} – множество натуральных чисел; Z={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все натуральные числа и числа,
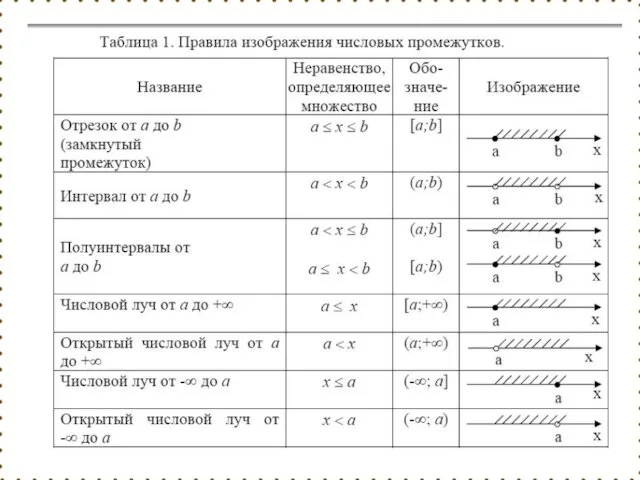
- 21. Действительные числа изображаются точками координатной прямой (числовой оси). Координатная прямая – это всякая прямая (обычно горизонтальная),
- 24. Поставьте вместо звездочки знак так, чтобы получить правильное утверждение: 5 * N; – 5 * Q;
- 29. задания:
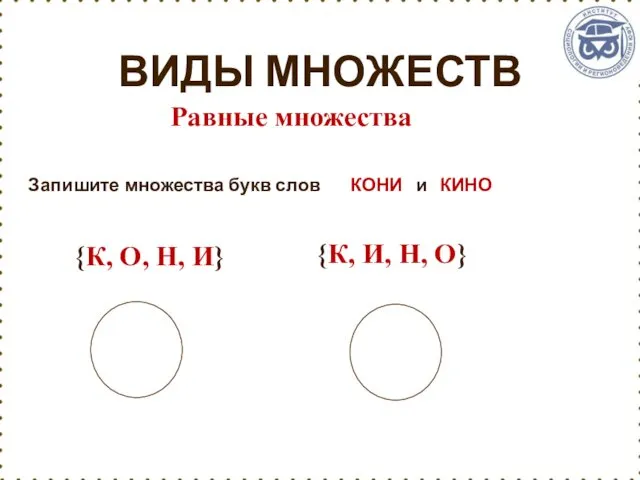
- 30. ВИДЫ МНОЖЕСТВ Запишите множества букв слов КОНИ и КИНО Равные множества {К, О, Н, И} {К,
- 31. Множества, состоящие из одних и тех же Элементов называют равными (одинаковыми). Пишут А=В ВИДЫ МНОЖЕСТВ
- 32. ВИДЫ МНОЖЕСТВ А = {2; 3; 5; 7; 11; 13}; В = {х | 5 Конечные
- 33. ВИДЫ МНОЖЕСТВ А = {1; 4; 9; 16; 25; …}; С = {10; 20; 30; 40;
- 34. Среди перечисленных ниже множеств укажите конечные и бесконечные множества: а) множество чисел, кратных 13; б) множество
- 35. А). Задайте множество цифр, с помощью которых записывается число: а) 3254; б) 8797; в) 11000; г)
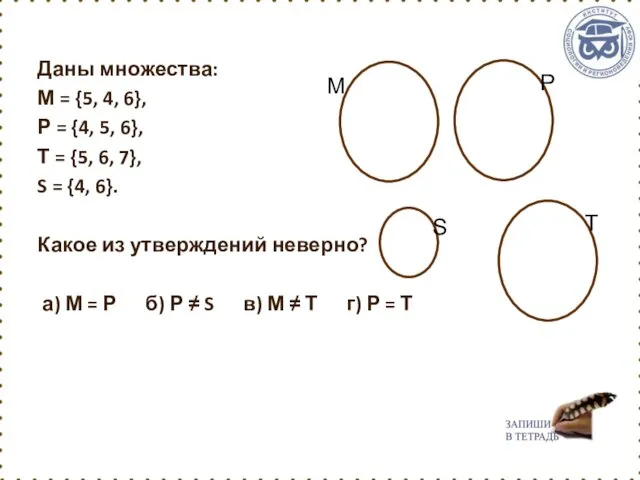
- 36. Даны множества: М = {5, 4, 6}, Р = {4, 5, 6}, Т = {5, 6,
- 37. Мощность множества Определение: Число элементов конечного множества называют мощностью множества и обозначают символом Card A или
- 38. В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества.
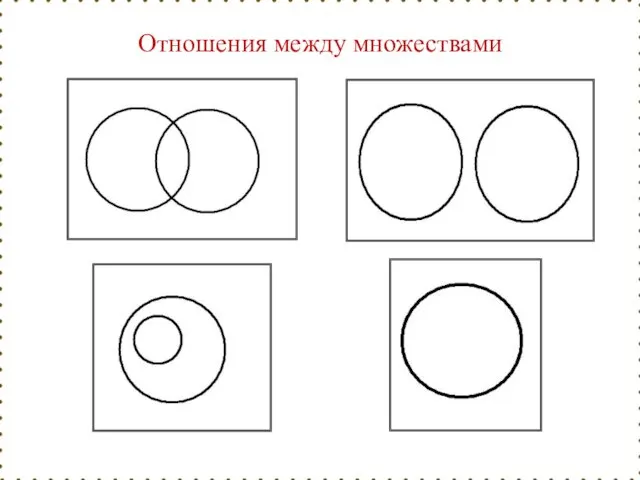
- 39. Отношения между множествами Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или
- 40. Отношения между множествами
- 41. При графическом изображении множеств удобно использовать диаграммы Венна, на которых универсальное множество обычно представляют в виде
- 42. Определение: Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При
- 43. Задание: Определить как между собой соотносятся множества A = {1, 2, 3, 5, 7}, и B
- 44. Количество подмножеств Определение: Если мощность множества n, то у этого множества 2n подмножеств. Пример: А={1,2} Подмножества
- 45. Определить количество подмножеств 1. В={1,3,5} 2. С={а,и,е,о}
- 46. Количество подмножеств В={1,3,5} Подмножества В: {∅}, {1}, {3}, {5}, {1,3}, {1,5}, {5,3}, {1,3,5} С={а,и,е,о} Подмножества С:
- 49. Пусть А — множество простых чисел вида 7n + 2, где n ∈ N. Верна ли
- 50. Задайте перечислением элементов множество, заданное характеристическим свойством
- 51. В множестве {лев; лисица; гиена; слон; рысь} все элементы, кроме одного, обладают некоторым свойством. а) опишите
- 52. Операции над множествами Два множества А и В равны (А=В), если они состоят из одних и
- 53. определение: Два множества А и В называются равными ( А = В ), если они состоят
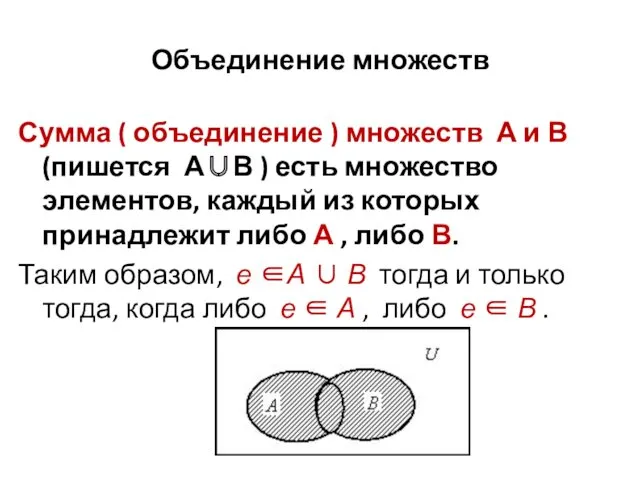
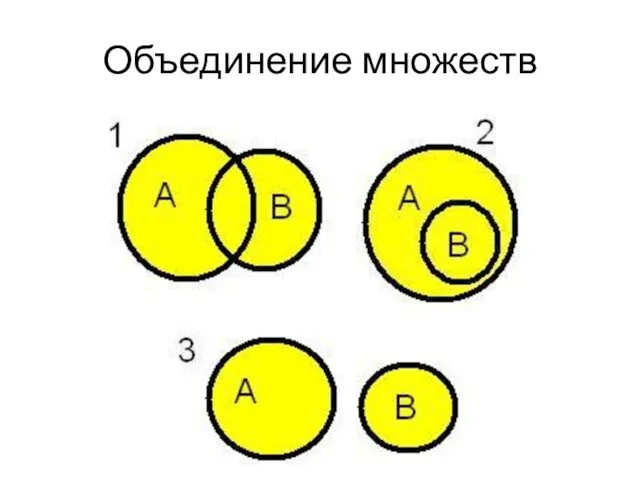
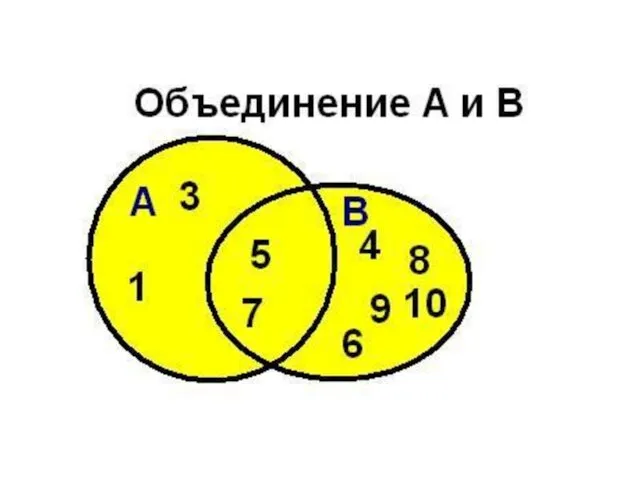
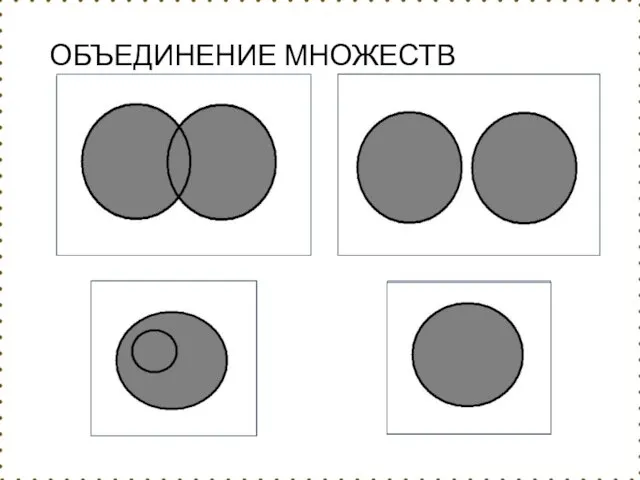
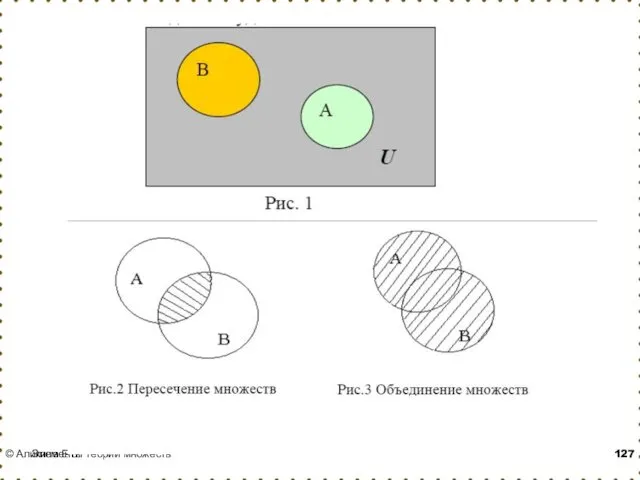
- 54. Объединение множеств Сумма ( объединение ) множеств А и В (пишется А∪В ) есть множество элементов,
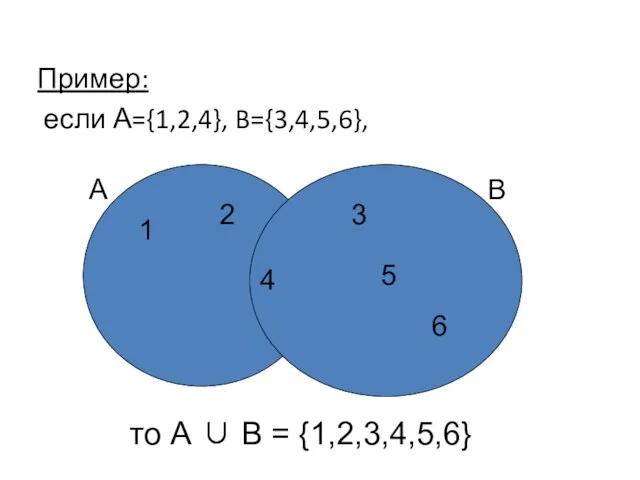
- 55. Пример: если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6} 1 2 4 А 4 3
- 56. Объединение множеств
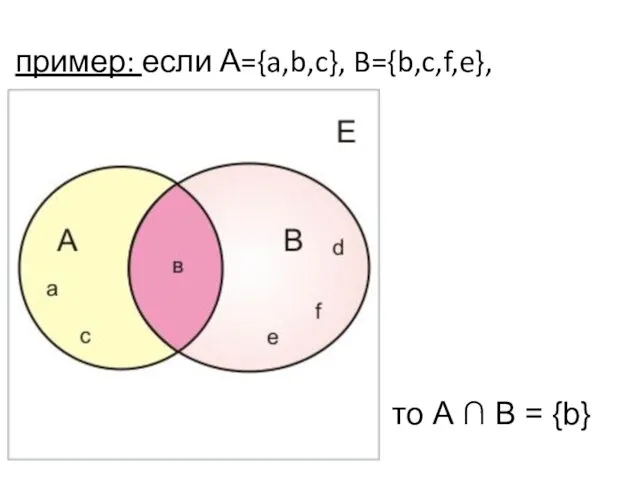
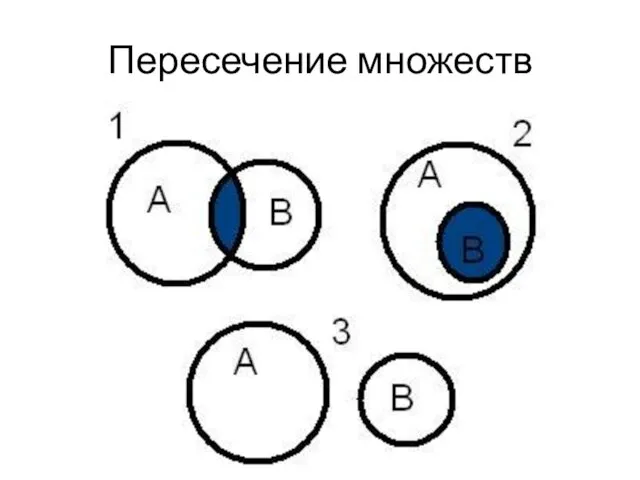
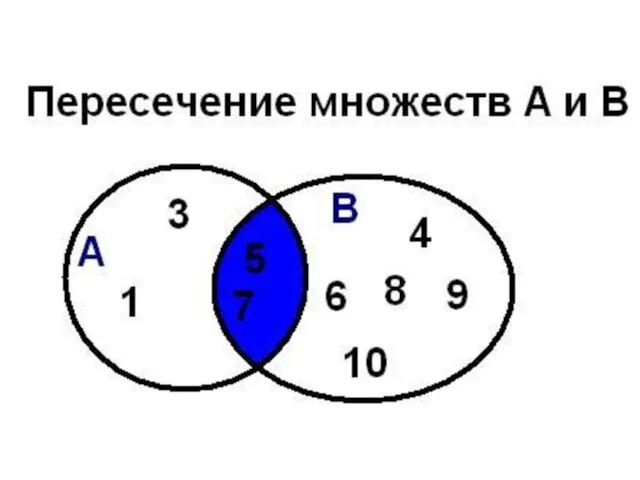
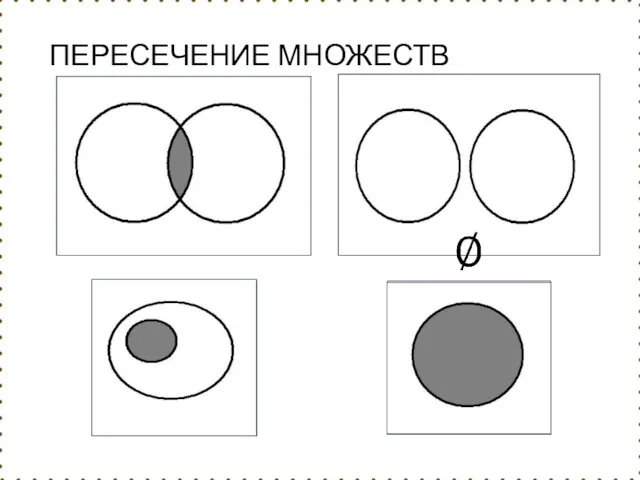
- 57. Операции над множествами Определение: Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы
- 58. пример: если А={a,b,c}, B={b,c,f,e}, то А ∩ В = {b}
- 59. Пересечение множеств
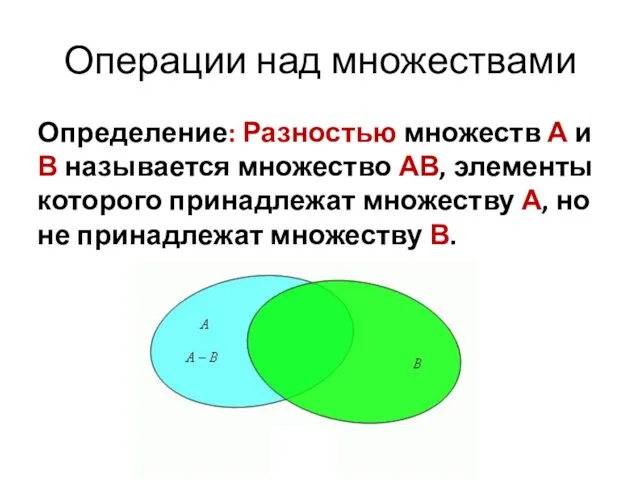
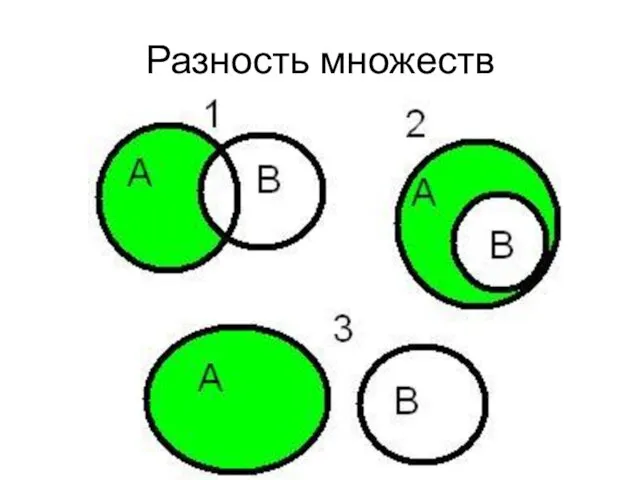
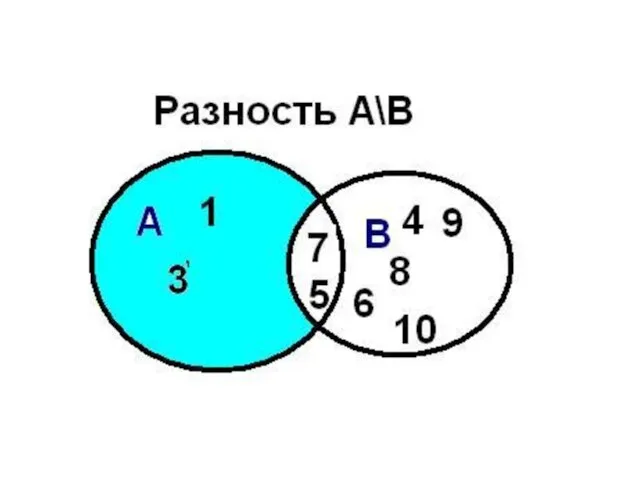
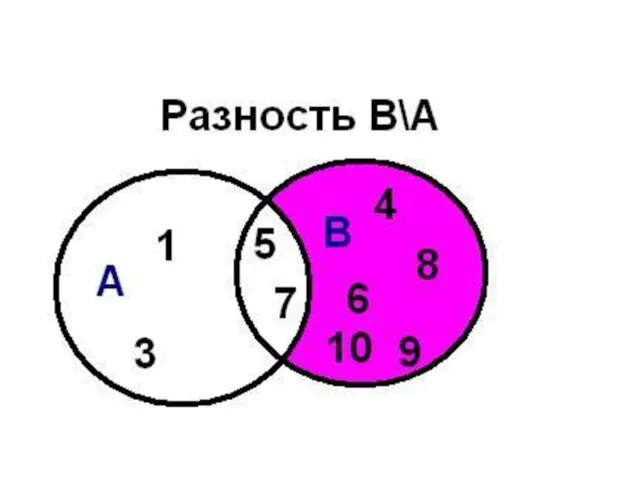
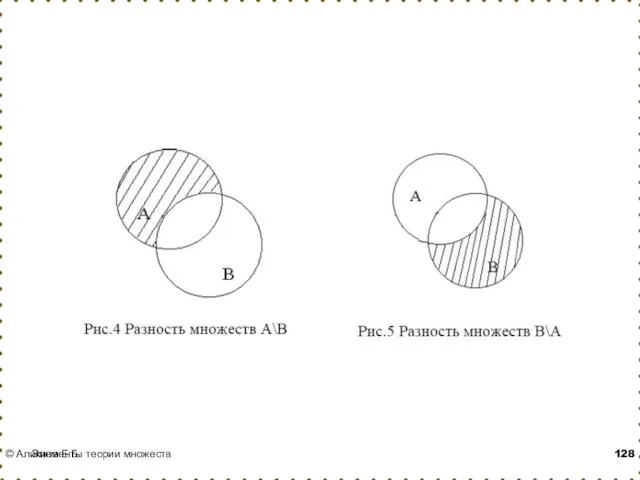
- 60. Операции над множествами Определение: Разностью множеств А и В называется множество АВ, элементы которого принадлежат множеству
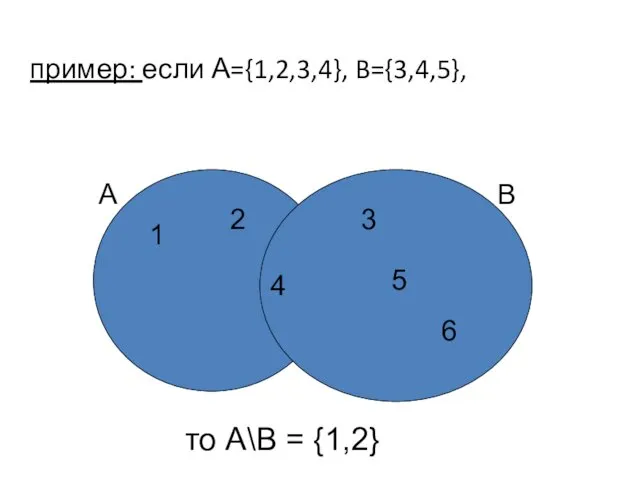
- 61. пример: если А={1,2,3,4}, B={3,4,5}, то А\В = {1,2} 1 2 4 А 4 3 5 6
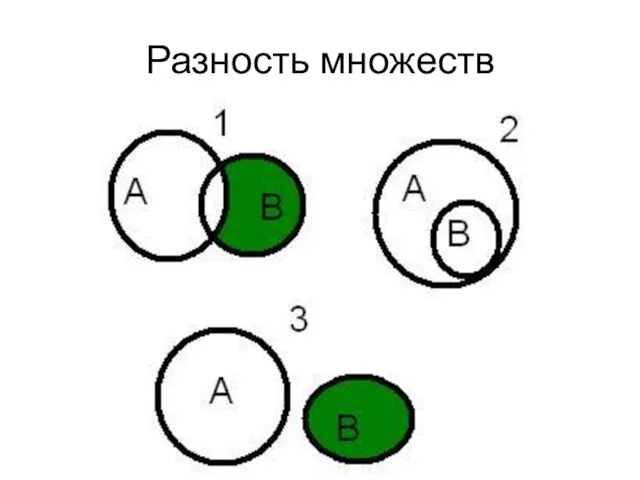
- 62. Разность множеств
- 63. Разность множеств
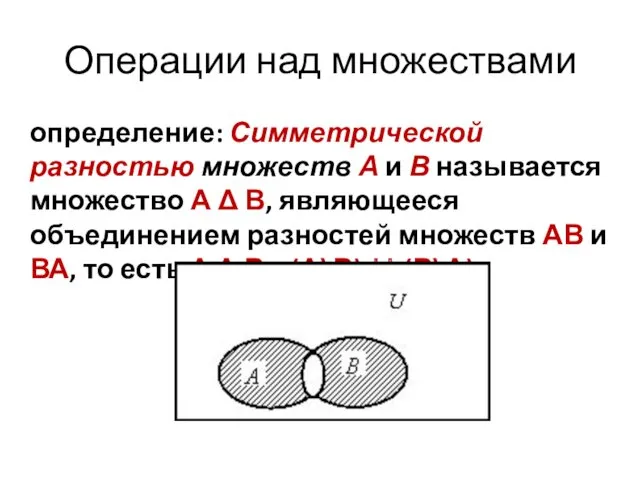
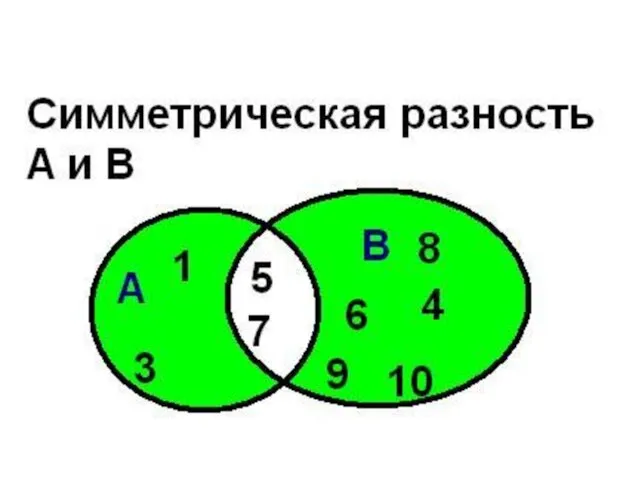
- 64. Операции над множествами определение: Симметрической разностью множеств А и В называется множество А Δ В, являющееся
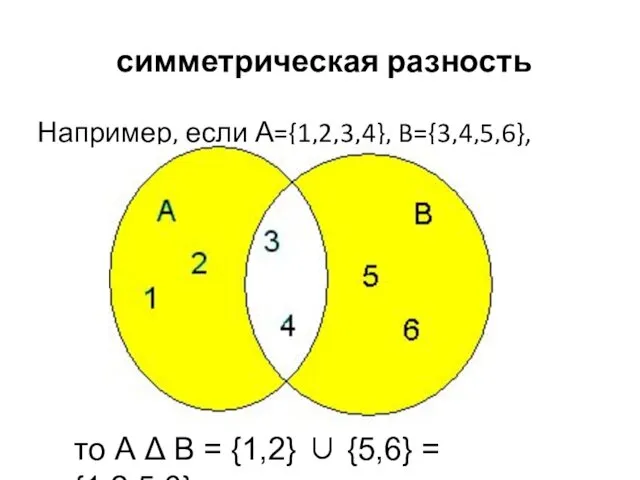
- 65. симметрическая разность Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
- 66. Симметричная разность
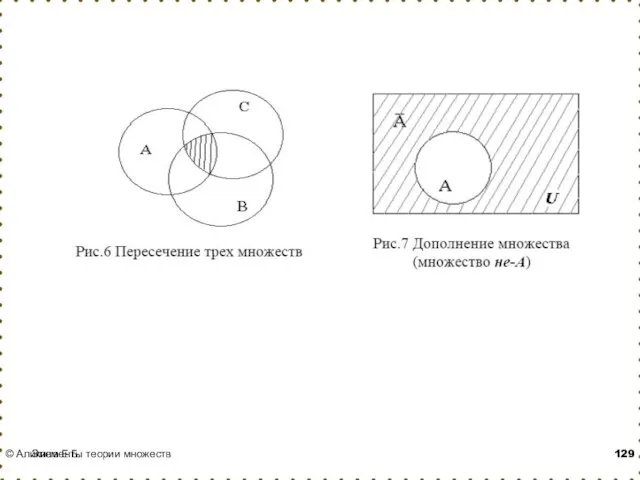
- 67. Операции над множествами Определение: Абсолютным дополнением множества называется множество всех элементов, не принадлежащих A, т.е. множество
- 68. Свойства операций над множествами:
- 69. П р и м е р ы Множество детей является подмножеством всего населения. Пересечением множества целых
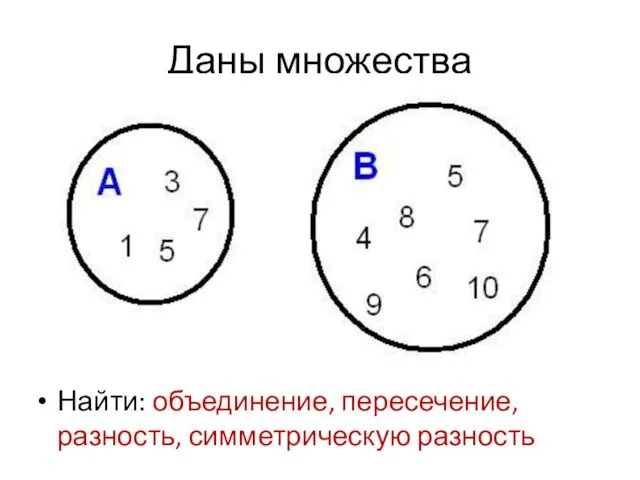
- 70. Даны множества Найти: объединение, пересечение, разность, симметрическую разность
- 76. Пример: На вступительном экзамене были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов
- 77. Решение. Пусть U — множество всех абитуриентов, А-множество абитуриентов, решивших задачу по алгебре, В-множество абитуриентов, решивших
- 78. Упорядоченная пара. Декартово произведение двух множеств
- 79. 1. Упорядоченная пара. Декартово произведение двух множеств 2. Соответствие между элементами множеств. 3. Способы задания соответствий
- 80. Рассмотрим задачу: используя цифры 1, 2, 3, нужно образовать все возможные двузначные числа. Запись каждого числа
- 81. Определение. Пары (а; b) и (с; d) равны тогда и только тогда, когда а = с
- 82. Определение. Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А,
- 83. Декартово произведение множеств есть множество, поэтому, как и всякое множество, его можно задать перечислением и указанием
- 84. Соответствие между элементами множеств Способы задания соответствий
- 85. Учащимся некоторого класса был задан вопрос, какие кружки они посещают. Их ответы были занесены в таблицу:
- 86. При помощи слов «посещать какой-либо кружок» между элементами этих множеств установлена некоторая связь, или, как говорят
- 87. Определение. Соответствием между множествами Х и Y называется любое подмножество R декартова произведения множеств Х и
- 88. Определение. Множество всех первых компонент пар, входящих в соответствие, называется областью определения соответствия. Определение. Множество всех
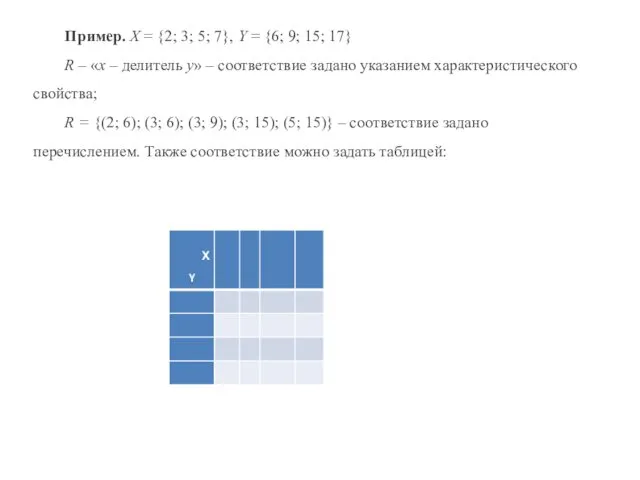
- 89. Пример. Х = {2; 3; 5; 7}, Y = {6; 9; 15; 17} R – «х
- 90. В нашем примере элементу 3 соответствует три элемента множества Y – 6, 9 и 15. Множество,
- 91. Определение. Множество всех элементов из множества Х, имеющих непустые образы, называется областью (множеством) определения соответствия R.
- 92. Взаимно однозначное соответствие
- 93. Определение. Отображением f множества Х в множество Y называется такое соответствие между множествами Х и Y,
- 94. Определение. Отображение, обладающее свойствами инъективности и сюръективности, называется взаимно однозначным. Другими словами: отображение f множества Х
- 96. ОБЪЕДИНЕНИЕ МНОЖЕСТВ
- 97. А – четные натуральные числа В – двузначные числа Найти объединение этих множеств. А В –
- 98. Определение: Пересечением множеств А и В называется множество, содержащее все элементы, которые принадлежат множествам А и
- 99. ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
- 100. А – четные натуральные числа В – двузначные числа Найти пересечение этих множеств. А В –
- 101. БЛИЦ-ОПРОС
- 102. БЛИЦ-ОПРОС земноводные, млекопитающие, хладнокровные и т.п. Какие названия применяются для обозначения множеств животных?
- 103. БЛИЦ-ОПРОС рота, взвод, полк, дивизия и т.п. Какие названия применяются для обозначения множеств военно-служащих?
- 104. БЛИЦ-ОПРОС букет Как называется множество цветов, стоящих в вазе?
- 105. БЛИЦ-ОПРОС экватор Как называется множество точек земной поверхности, равноудаленных от обоих полюсов?
- 106. БЛИЦ-ОПРОС деревня, село, город, посёлок Как называется множество населённых людьми мест?
- 107. БЛИЦ-ОПРОС выставка, галерея Как называется множество картин?
- 108. БЛИЦ-ОПРОС архив Как называется множество документов?
- 109. БЛИЦ-ОПРОС флотилия, эскадра Какие названия применяют для обозначения множеств кораблей?
- 110. Даны множества: А = {2; 3; 8}, В = {2; 3; 8; 11}, С = {5;
- 111. Даны множества: А = {a, b, c, d}, B = {c, d, e, f}, C =
- 112. Даны множества: А – множество всех натуральных чисел, кратных 10, В = {1; 2; 3;…, 41}.
- 113. k Решение задачи с помощью кругов Эйлера Леона́рд Э́йлер — швейцарский, немецкий и российский математик, внёсший
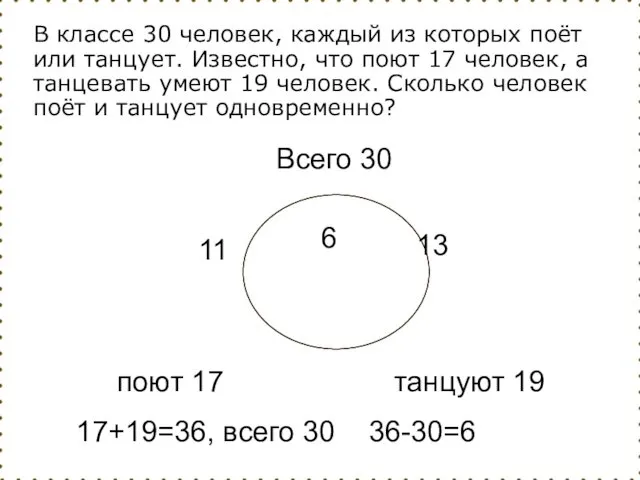
- 114. поют 17 танцуют 19 Всего 30 17+19=36, всего 30 36-30=6 6 11 13 В классе 30
- 115. Решение Пусть А - это множество учеников, умеющих петь. Количество элементов в нём по условию равно
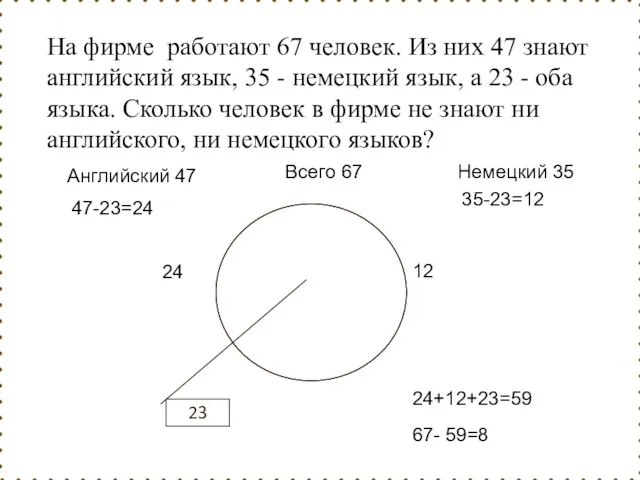
- 116. Всего 67 Английский 47 Немецкий 35 23 47-23=24 24 35-23=12 12 24+12+23=59 67- 59=8 На фирме
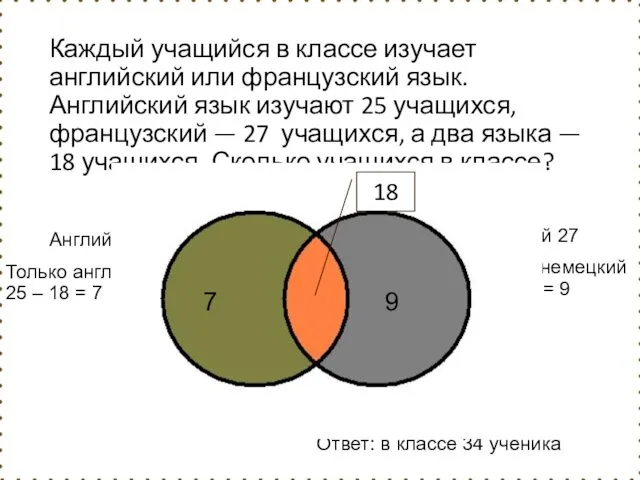
- 117. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский —
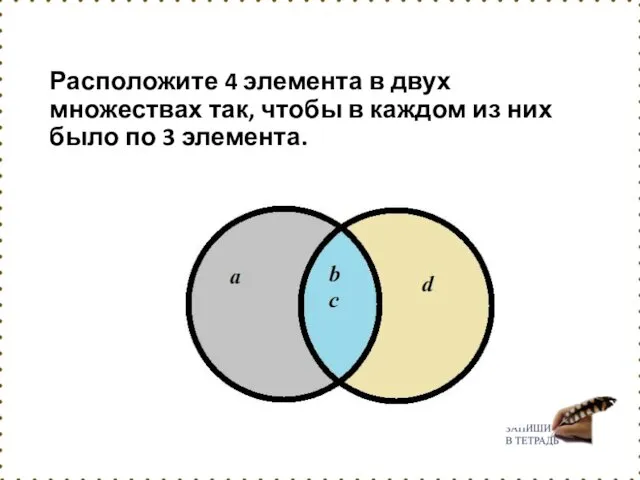
- 118. Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента.
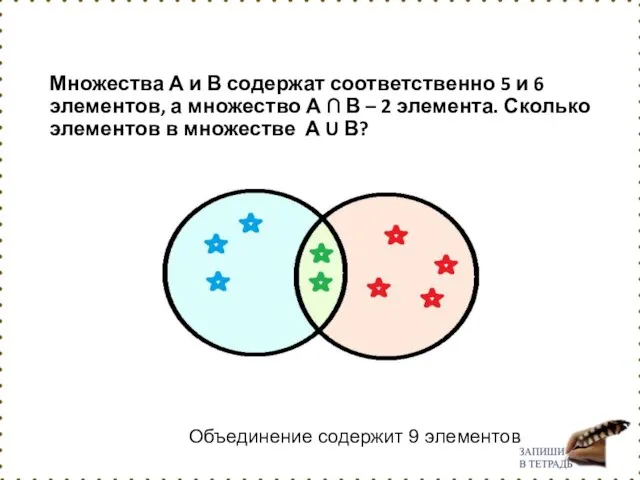
- 119. Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В –
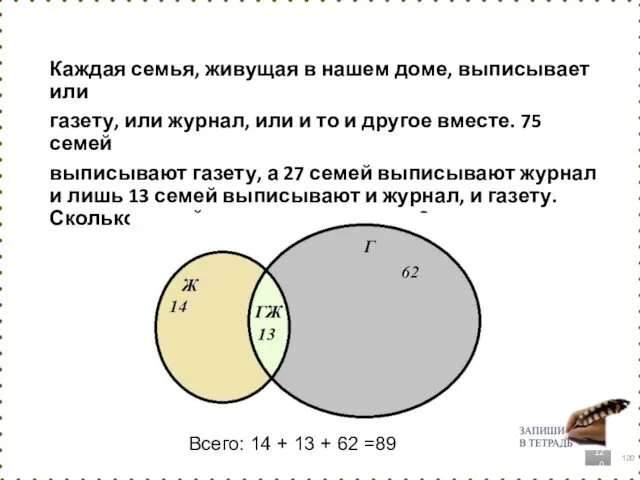
- 120. Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое
- 121. На школьной спартакиаде каждый из 25 учеников 9 –го класса выполнил норматив или по бегу, или
- 122. Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки.
- 123. Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли
- 124. В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 –
- 125. УМЕНИЯ ЗНАНИЯ МНОЖЕСТВО ЭЛЕМЕНТ МНОЖЕСТВА ВИДЫ МНОЖЕСТВ ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ ОБЪЕДИНЕНИЕ МНОЖЕСТВ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ НАХОДИТЬ ОБЪЕДИНЕНИЕ
- 126. Диаграммы Эйлера-Венна Для наглядного представления множеств и результатов операций над ними удобно пользоваться диаграммами Эйлера-Венна (кругами
- 127. © Аликина Е.Б. Элементы теории множеств
- 128. © Аликина Е.Б. Элементы теории множеств
- 129. © Аликина Е.Б. Элементы теории множеств
- 130. Формула для подсчета числа элементов в объединении трех множеств: m (А∪В∪С) = m (А) + m
- 131. Примеры Пример 1. Записать множество всех натуральных делителей числа 15 и найти число его элементов. Решение:
- 132. Пример 2 Даны множества А={2, 3, 5, 8, 13, 15}, В={1, 3, 4, 8,16}, С={12, 13,
- 133. Пример 3. Экзамен по математике сдавали 250 абитуриентов, оценку ниже пяти получили 180 человек, а выдержали
- 134. Пример 4. В школе 1400 учеников. Из них 1250 умеют кататься на лыжах, 952 – на
- 135. © Аликина Е.Б. Элементы теории множеств
- 136. Учащиеся, не умеющие кататься ни на лыжах, ни на коньках, составляют множество А’∩В’= (А∪B)’ m (А∪B)
- 138. Скачать презентацию


































































































 Кривые второго порядка
Кривые второго порядка Масштаб. Урок математики в 6 классе
Масштаб. Урок математики в 6 классе Понятие одночлена. Стандартный вид одночлена
Понятие одночлена. Стандартный вид одночлена Геометричні перетворення
Геометричні перетворення Сравнение дробей
Сравнение дробей Задачи на нахождение суммы и разности
Задачи на нахождение суммы и разности Мощность статистического теста. Дисперсионный анализ ANOVA. Занятие 3
Мощность статистического теста. Дисперсионный анализ ANOVA. Занятие 3 Линейная парная регрессия
Линейная парная регрессия Узоры и орнаменты
Узоры и орнаменты Презентация компьютерной программы Занимательная математика
Презентация компьютерной программы Занимательная математика Обыкновенные дроби. Выполните действия
Обыкновенные дроби. Выполните действия Проект по математике
Проект по математике Діофантові рівняння
Діофантові рівняння Өрнектегі композиция
Өрнектегі композиция Деление и умножение чисел. Дидактическая игра
Деление и умножение чисел. Дидактическая игра Многогранники. Урок 1. Определение и виды многогранников. Геометрия. 10 класс
Многогранники. Урок 1. Определение и виды многогранников. Геометрия. 10 класс Измерение отрезков и углов
Измерение отрезков и углов Решение простейших тригонометрических уравнений. 10 класс
Решение простейших тригонометрических уравнений. 10 класс Математика вокруг нас. Проект Числа в загадках, пословицах и поговорках
Математика вокруг нас. Проект Числа в загадках, пословицах и поговорках Введение в теорию пределов
Введение в теорию пределов Табличное умножение и деление. Игры-тренажёры
Табличное умножение и деление. Игры-тренажёры Булева алгебра. Основные понятия булевой алгебры
Булева алгебра. Основные понятия булевой алгебры Решение заданий С1 на ЕГЭ
Решение заданий С1 на ЕГЭ Математика. Структура экзамена
Математика. Структура экзамена Измерение отрезков
Измерение отрезков Игра Я знаю всё
Игра Я знаю всё Додавання та віднімання дробів з різними знаменниками
Додавання та віднімання дробів з різними знаменниками Тест по геометрии
Тест по геометрии