- Главная
- Математика
- Prime numbers. Euclid's algorithm

Содержание
- 2. A prime number - it is a natural number greater than one that has exactly two
- 4. All other numbers not equal to unity, are called composite. Thus, all integers except one, are
- 5. Euclid's algorithm - an efficient algorithm for finding the greatest common divisor of two integers (or
- 6. Euclidean Algorithm - Given a, b ∈ Z, not both 0, find (a, b) • Step
- 8. Скачать презентацию
Слайд 2
A prime number - it is a natural number greater than
A prime number - it is a natural number greater than
one that has exactly two positive divisors: 1 and itself. The study deals with the properties of prime numbers theory of numbers. A prime number is an integer p > 1 such that it cannot be written as p = ab with a, b > 1.
Example: 7 is prime because the only numbers that will divide into it evenly are 1 and 7.
Example: 7 is prime because the only numbers that will divide into it evenly are 1 and 7.
Слайд 3
Слайд 4
All other numbers not equal to unity, are called composite. Thus,
All other numbers not equal to unity, are called composite. Thus,
all integers except one, are divided into simple and complex. The study deals with the properties of prime numbers theory of numbers. The theory of rings primes correspond to the irreducible elements.
Слайд 5
Euclid's algorithm - an efficient algorithm for finding the greatest common
Euclid's algorithm - an efficient algorithm for finding the greatest common
divisor of two integers (or a common measure of two segments). The algorithm is named for the Greek mathematician Euclid, who first described it in the VII and X book "Principia." In the simplest case, Euclid's algorithm is applied to a pair of positive integers, and generates a new pair consisting of a smaller number, and the difference between larger and smaller integer. The process is repeated until the numbers become equal. The obtained number is the greatest common divisor of the original pair.
Слайд 6
Euclidean Algorithm - Given a, b ∈ Z, not both 0,
Euclidean Algorithm - Given a, b ∈ Z, not both 0,
find (a, b)
• Step 1: If a, b < 0, replace with negative
• Step 2: If a > b, switch a and b
• Step 3: If a = 0, return b
• Step 4: Since a > 0, write b = aq + r with 0 ≤ r < a. Replace (a, b) with (r, a) and go to Step 3
• Step 1: If a, b < 0, replace with negative
• Step 2: If a > b, switch a and b
• Step 3: If a = 0, return b
• Step 4: Since a > 0, write b = aq + r with 0 ≤ r < a. Replace (a, b) with (r, a) and go to Step 3
- Предыдущая
Марк Твен (Сэмюэл Лэнгхорн Клеменс)Следующая -
Recitation class




 Единицы длины
Единицы длины Без знания дробей никто не может признаваться знающим математику
Без знания дробей никто не может признаваться знающим математику Скалярное произведение векторов
Скалярное произведение векторов Сказка Родственники
Сказка Родственники Уравнение плоскости, проходящей через три точки
Уравнение плоскости, проходящей через три точки Название компонентов действий
Название компонентов действий Диаграммы
Диаграммы Тест по математике Реши пример Диск
Тест по математике Реши пример Диск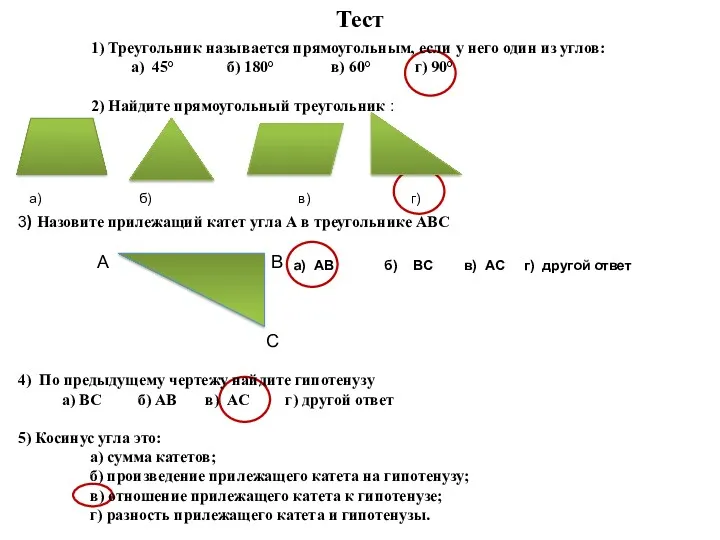 Тест. Прямоугольный треугольник
Тест. Прямоугольный треугольник Описательная статистика. Выборочный метод
Описательная статистика. Выборочный метод Нод по сенсорному развитию Паровозик из Ромашкова
Нод по сенсорному развитию Паровозик из Ромашкова Лабораторная № 6. Численное решение систем линейных алгебраических уравнений
Лабораторная № 6. Численное решение систем линейных алгебраических уравнений Игра Поле математических чудес.
Игра Поле математических чудес. Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Работа с одаренными (или имеющими склонностями) детьми по математическому развитию
Работа с одаренными (или имеющими склонностями) детьми по математическому развитию Построение сечения многогранника плоскостью
Построение сечения многогранника плоскостью Формула Байеса. Независимые события
Формула Байеса. Независимые события Линейные дискретные системы. Структура звеньев второго порядка
Линейные дискретные системы. Структура звеньев второго порядка Методика обучения математике для формирования у младших школьников коммуникативных УУД
Методика обучения математике для формирования у младших школьников коммуникативных УУД Презентация 3 класс Умножение на трёхзначное число
Презентация 3 класс Умножение на трёхзначное число Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 15
Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 15 В гостях у Мнемозины
В гостях у Мнемозины Интегральное исчисление. Первообразная и неопределенный интеграл
Интегральное исчисление. Первообразная и неопределенный интеграл Кеңістіктегі жазықтық пен түзудің теңдеулері
Кеңістіктегі жазықтық пен түзудің теңдеулері Приближенные значения действительных чисел
Приближенные значения действительных чисел Перпендикулярность прямых и плоскостей в пространстве
Перпендикулярность прямых и плоскостей в пространстве Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия
Презентация для учащихся 2 класса по математике (автор Л.Г. Петерсон) Такая загадочная Индия Тест. Задания В10, ЕГЭ по математике
Тест. Задания В10, ЕГЭ по математике